A Simple Zero-shot Prompt Weighting Technique to Improve Prompt Ensembling in Text-Image Models

Contrastively trained text-image models have the remarkable ability to perform zero-shot classification, that is, classifying previously unseen images into categories that the model has never been explicitly trained to identify. However, these zero-shot classifiers need prompt engineering to achieve high accuracy. Prompt engineering typically requires hand-crafting a set of prompts for individual downstream tasks. In this work, we aim to automate this prompt engineering and improve zero-shot accuracy through prompt ensembling. In particular, we ask "Given a large pool of prompts, can we automatically score the prompts and ensemble those that are most suitable for a particular downstream dataset, without needing access to labeled validation data?". We demonstrate that this is possible. In doing so, we identify several pathologies in a naive prompt scoring method where the score can be easily overconfident due to biases in pre-training and test data, and we propose a novel prompt scoring method that corrects for the biases. Using our proposed scoring method to create a weighted average prompt ensemble, our method outperforms equal average ensemble, as well as hand-crafted prompts, on ImageNet, 4 of its variants, and 11 fine-grained classification benchmarks, all while being fully automatic, optimization-free, and not requiring access to labeled validation data.

Pushing the Accuracy-Group Robustness Frontier with Introspective Self-play

Standard empirical risk minimization (ERM) training can produce deep neural network (DNN) models that are accurate on average but under-perform in under-represented population subgroups, especially when there are imbalanced group distributions in the long-tailed training data. Therefore, approaches that improve the accuracy-group robustness trade-off frontier of a DNN model (i.e. improving worst-group accuracy without sacrificing average accuracy, or vice versa) is of crucial importance. Uncertainty-based active learning (AL) can potentially improve the frontier by preferentially sampling underrepresented subgroups to create a more balanced training dataset. However, the quality of uncertainty estimates from modern DNNs tend to degrade in the presence of spurious correlations and dataset bias, compromising the effectiveness of AL for sampling tail groups. In this work, we propose Introspective Self-play (ISP), a simple approach to improve the uncertainty estimation of a deep neural network under dataset bias, by adding an auxiliary introspection task requiring a model to predict the bias for each data point in addition to the label. We show that ISP provably improves the bias-awareness of the model representation and the resulting uncertainty estimates. On two real-world tabular and language tasks, ISP serves as a simple "plug-in" for AL model training, consistently improving both the tail-group sampling rate and the final accuracy-fairness trade-off frontier of popular AL methods.

A Simple Approach to Improve Single-Model Deep Uncertainty via Distance-Awareness

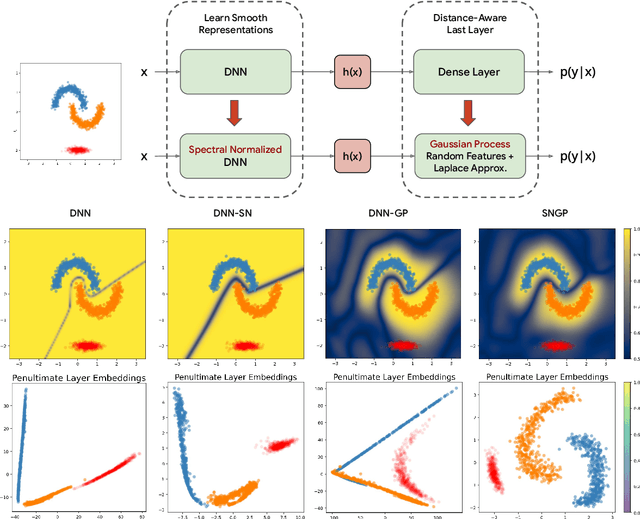
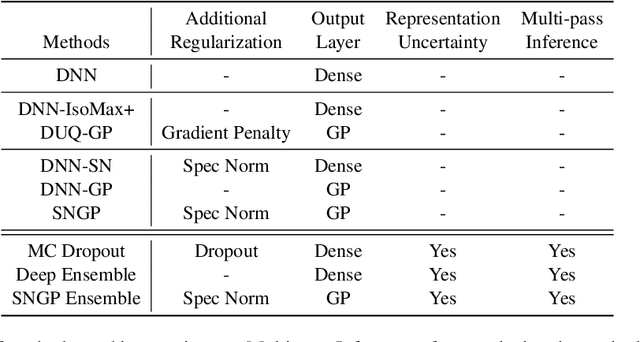
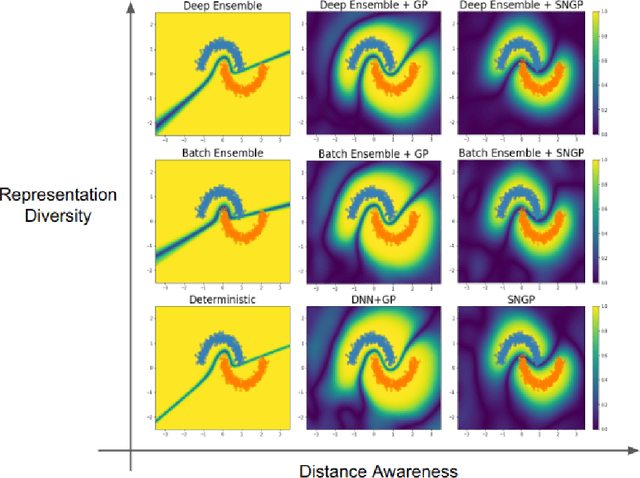
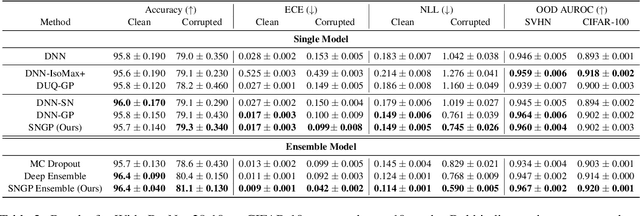
Accurate uncertainty quantification is a major challenge in deep learning, as neural networks can make overconfident errors and assign high confidence predictions to out-of-distribution (OOD) inputs. The most popular approaches to estimate predictive uncertainty in deep learning are methods that combine predictions from multiple neural networks, such as Bayesian neural networks (BNNs) and deep ensembles. However their practicality in real-time, industrial-scale applications are limited due to the high memory and computational cost. Furthermore, ensembles and BNNs do not necessarily fix all the issues with the underlying member networks. In this work, we study principled approaches to improve uncertainty property of a single network, based on a single, deterministic representation. By formalizing the uncertainty quantification as a minimax learning problem, we first identify distance awareness, i.e., the model's ability to quantify the distance of a testing example from the training data, as a necessary condition for a DNN to achieve high-quality (i.e., minimax optimal) uncertainty estimation. We then propose Spectral-normalized Neural Gaussian Process (SNGP), a simple method that improves the distance-awareness ability of modern DNNs with two simple changes: (1) applying spectral normalization to hidden weights to enforce bi-Lipschitz smoothness in representations and (2) replacing the last output layer with a Gaussian process layer. On a suite of vision and language understanding benchmarks, SNGP outperforms other single-model approaches in prediction, calibration and out-of-domain detection. Furthermore, SNGP provides complementary benefits to popular techniques such as deep ensembles and data augmentation, making it a simple and scalable building block for probabilistic deep learning. Code is open-sourced at https://github.com/google/uncertainty-baselines

Towards a Unified Framework for Uncertainty-aware Nonlinear Variable Selection with Theoretical Guarantees

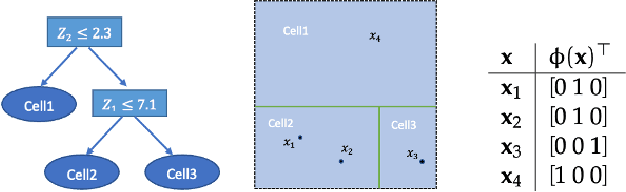
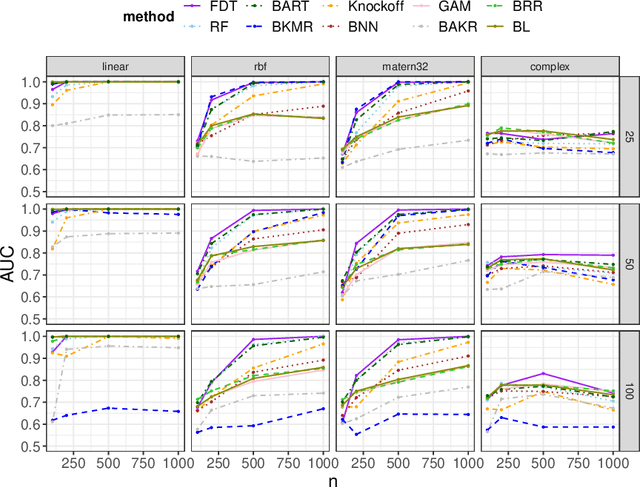
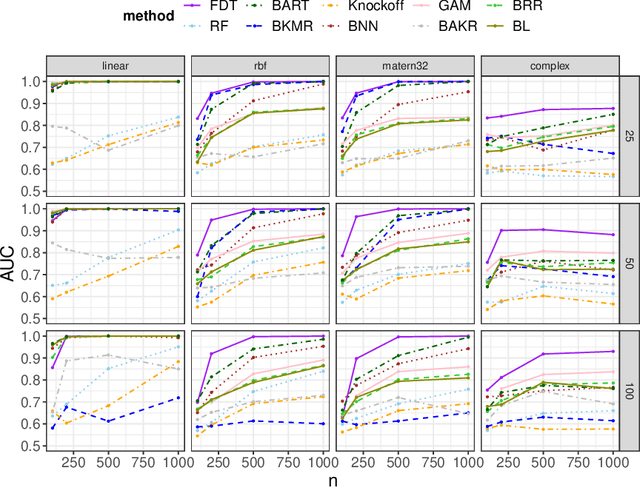
We develop a simple and unified framework for nonlinear variable selection that incorporates model uncertainty and is compatible with a wide range of machine learning models (e.g., tree ensembles, kernel methods and neural network). In particular, for a learned nonlinear model $f(\mathbf{x})$, we consider quantifying the importance of an input variable $\mathbf{x}^j$ using the integrated gradient measure $\psi_j = \Vert \frac{\partial}{\partial \mathbf{x}^j} f(\mathbf{x})\Vert^2_2$. We then (1) provide a principled approach for quantifying variable selection uncertainty by deriving its posterior distribution, and (2) show that the approach is generalizable even to non-differentiable models such as tree ensembles. Rigorous Bayesian nonparametric theorems are derived to guarantee the posterior consistency and asymptotic uncertainty of the proposed approach. Extensive simulation confirms that the proposed algorithm outperforms existing classic and recent variable selection methods.

Training independent subnetworks for robust prediction

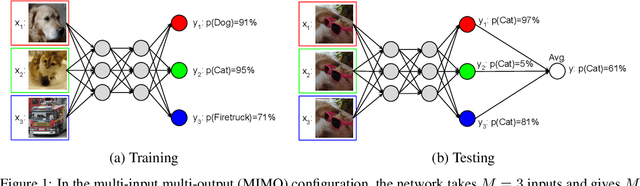
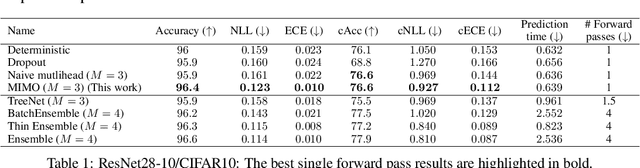
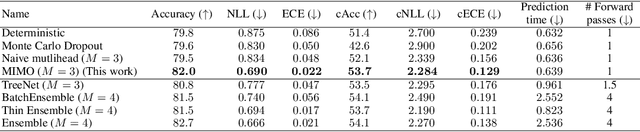
Recent approaches to efficiently ensemble neural networks have shown that strong robustness and uncertainty performance can be achieved with a negligible gain in parameters over the original network. However, these methods still require multiple forward passes for prediction, leading to a significant computational cost. In this work, we show a surprising result: the benefits of using multiple predictions can be achieved `for free' under a single model's forward pass. In particular, we show that, using a multi-input multi-output (MIMO) configuration, one can utilize a single model's capacity to train multiple subnetworks that independently learn the task at hand. By ensembling the predictions made by the subnetworks, we improve model robustness without increasing compute. We observe a significant improvement in negative log-likelihood, accuracy, and calibration error on CIFAR10, CIFAR100, ImageNet, and their out-of-distribution variants compared to previous methods.

Pruning Redundant Mappings in Transformer Models via Spectral-Normalized Identity Prior

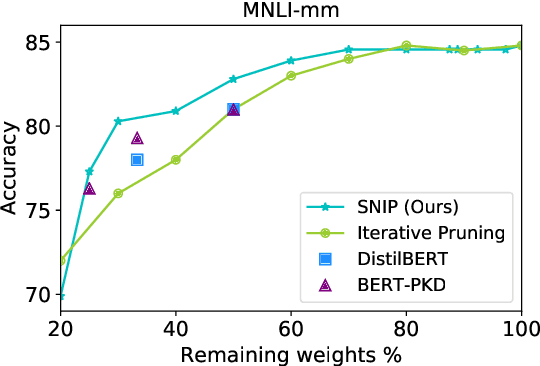
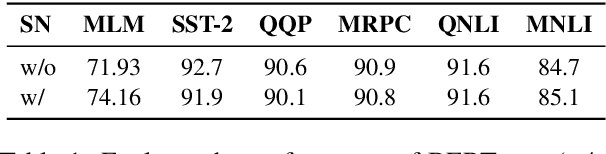
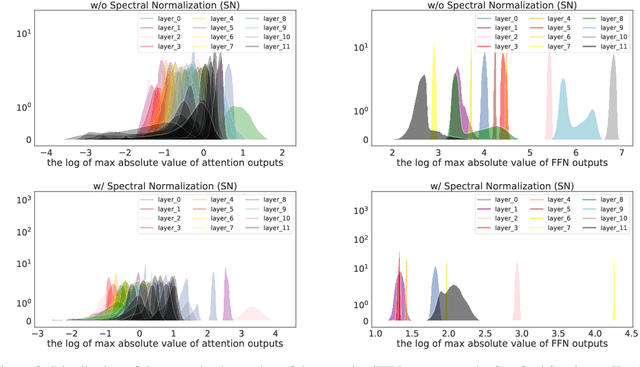
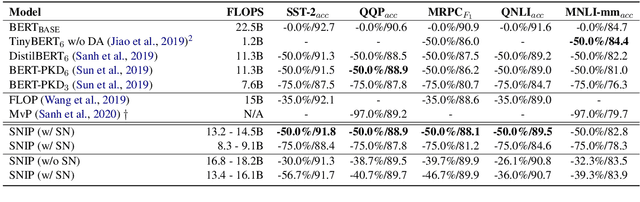
Traditional (unstructured) pruning methods for a Transformer model focus on regularizing the individual weights by penalizing them toward zero. In this work, we explore spectral-normalized identity priors (SNIP), a structured pruning approach that penalizes an entire residual module in a Transformer model toward an identity mapping. Our method identifies and discards unimportant non-linear mappings in the residual connections by applying a thresholding operator on the function norm. It is applicable to any structured module, including a single attention head, an entire attention block, or a feed-forward subnetwork. Furthermore, we introduce spectral normalization to stabilize the distribution of the post-activation values of the Transformer layers, further improving the pruning effectiveness of the proposed methodology. We conduct experiments with BERT on 5 GLUE benchmark tasks to demonstrate that SNIP achieves effective pruning results while maintaining comparable performance. Specifically, we improve the performance over the state-of-the-art by 0.5 to 1.0% on average at 50% compression ratio.

Simple and Principled Uncertainty Estimation with Deterministic Deep Learning via Distance Awareness

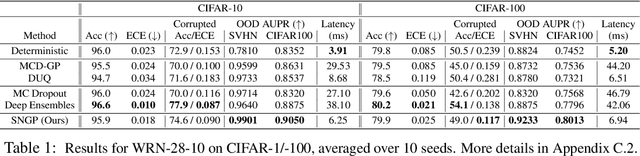
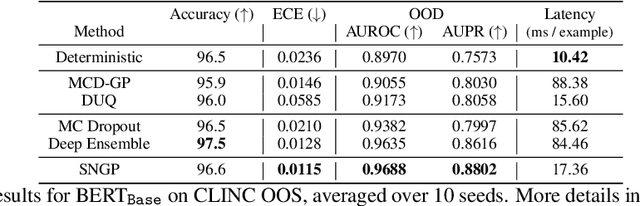
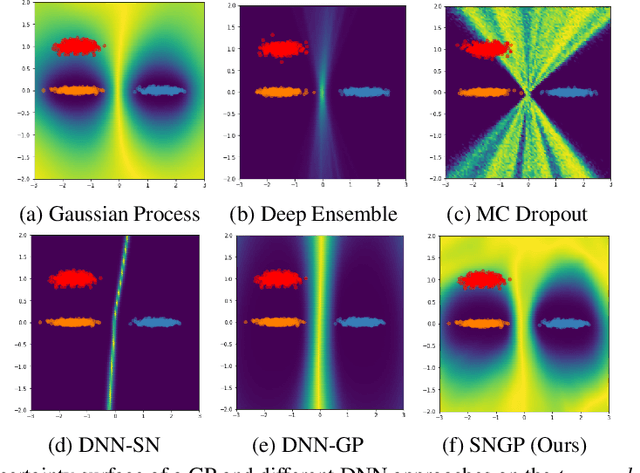
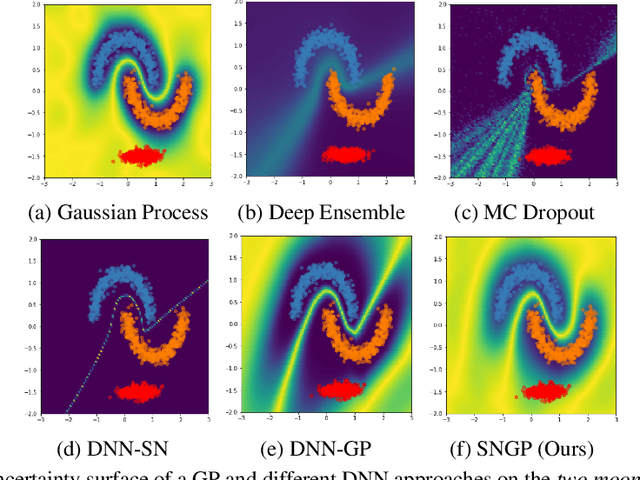
Bayesian neural networks (BNN) and deep ensembles are principled approaches to estimate the predictive uncertainty of a deep learning model. However their practicality in real-time, industrial-scale applications are limited due to their heavy memory and inference cost. This motivates us to study principled approaches to high-quality uncertainty estimation that require only a single deep neural network (DNN). By formalizing the uncertainty quantification as a minimax learning problem, we first identify input distance awareness, i.e., the model's ability to quantify the distance of a testing example from the training data in the input space, as a necessary condition for a DNN to achieve high-quality (i.e., minimax optimal) uncertainty estimation. We then propose Spectral-normalized Neural Gaussian Process (SNGP), a simple method that improves the distance-awareness ability of modern DNNs, by adding a weight normalization step during training and replacing the output layer with a Gaussian process. On a suite of vision and language understanding tasks and on modern architectures (Wide-ResNet and BERT), SNGP is competitive with deep ensembles in prediction, calibration and out-of-domain detection, and outperforms the other single-model approaches.

Variable Selection with Rigorous Uncertainty Quantification using Deep Bayesian Neural Networks: Posterior Concentration and Bernstein-von Mises Phenomenon

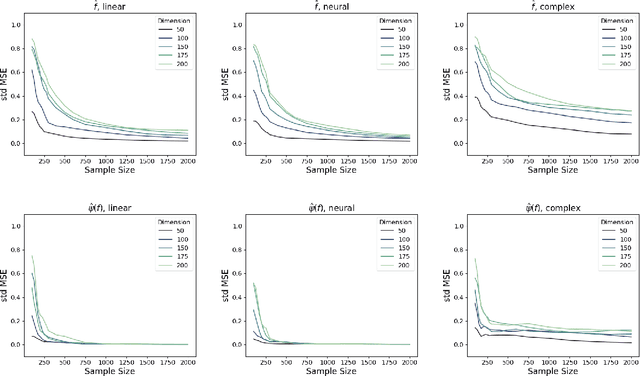
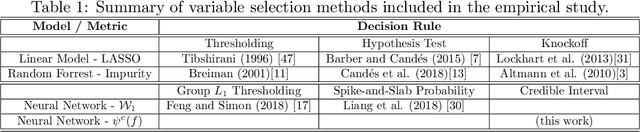
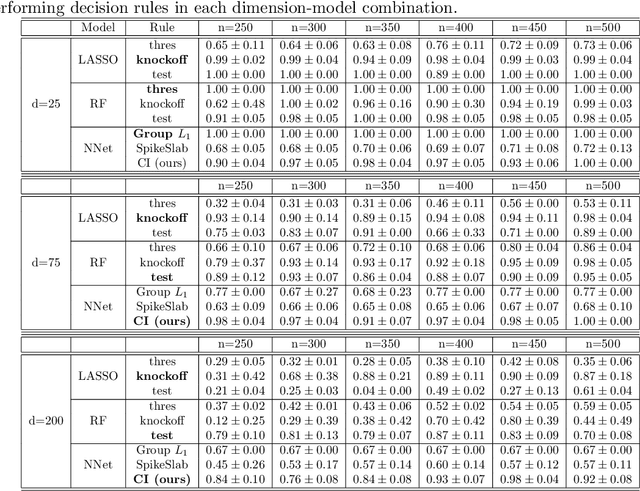
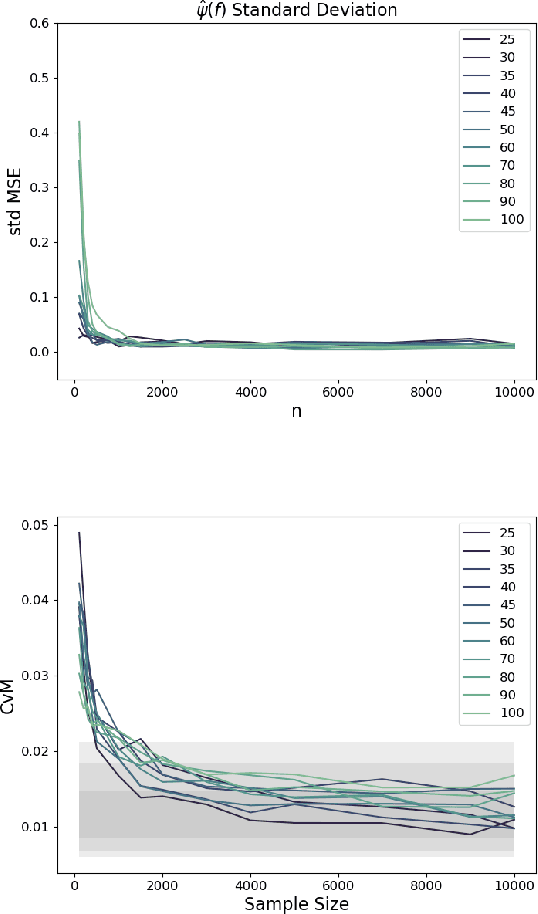
This work develops rigorous theoretical basis for the fact that deep Bayesian neural network (BNN) is an effective tool for high-dimensional variable selection with rigorous uncertainty quantification. We develop new Bayesian non-parametric theorems to show that a properly configured deep BNN (1) learns the variable importance effectively in high dimensions, and its learning rate can sometimes "break" the curse of dimensionality. (2) BNN's uncertainty quantification for variable importance is rigorous, in the sense that its 95% credible intervals for variable importance indeed covers the truth 95% of the time (i.e., the Bernstein-von Mises (BvM) phenomenon). The theoretical results suggest a simple variable selection algorithm based on the BNN's credible intervals. Extensive simulation confirms the theoretical findings and shows that the proposed algorithm outperforms existing classic and neural-network-based variable selection methods, particularly in high dimensions.

Accurate Uncertainty Estimation and Decomposition in Ensemble Learning

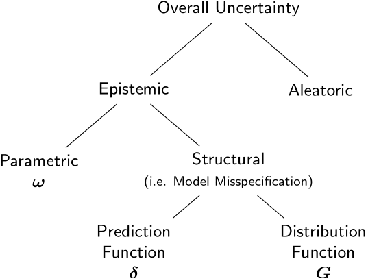
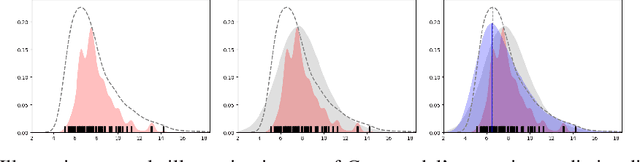
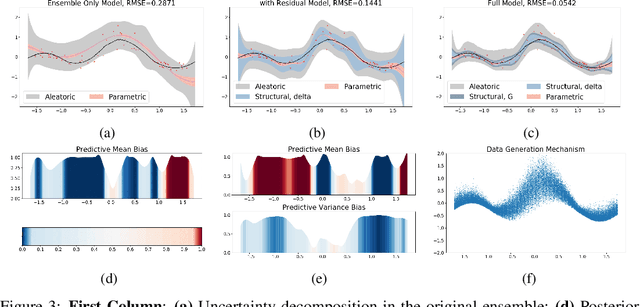
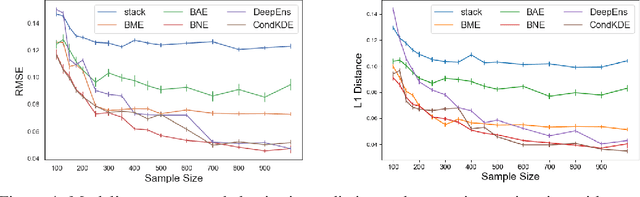
Ensemble learning is a standard approach to building machine learning systems that capture complex phenomena in real-world data. An important aspect of these systems is the complete and valid quantification of model uncertainty. We introduce a Bayesian nonparametric ensemble (BNE) approach that augments an existing ensemble model to account for different sources of model uncertainty. BNE augments a model's prediction and distribution functions using Bayesian nonparametric machinery. It has a theoretical guarantee in that it robustly estimates the uncertainty patterns in the data distribution, and can decompose its overall predictive uncertainty into distinct components that are due to different sources of noise and error. We show that our method achieves accurate uncertainty estimates under complex observational noise, and illustrate its real-world utility in terms of uncertainty decomposition and model bias detection for an ensemble in predict air pollution exposures in Eastern Massachusetts, USA.

Gaussian Process Regression and Classification under Mathematical Constraints with Learning Guarantees

We introduce constrained Gaussian process (CGP), a Gaussian process model for random functions that allows easy placement of mathematical constrains (e.g., non-negativity, monotonicity, etc) on its sample functions. CGP comes with closed-form probability density function (PDF), and has the attractive feature that its posterior distributions for regression and classification are again CGPs with closed-form expressions. Furthermore, we show that CGP inherents the optimal theoretical properties of the Gaussian process, e.g. rates of posterior contraction, due to the fact that CGP is an Gaussian process with a more efficient model space.