A Simple Approach to Improve Single-Model Deep Uncertainty via Distance-Awareness
Paper and Code
May 01, 2022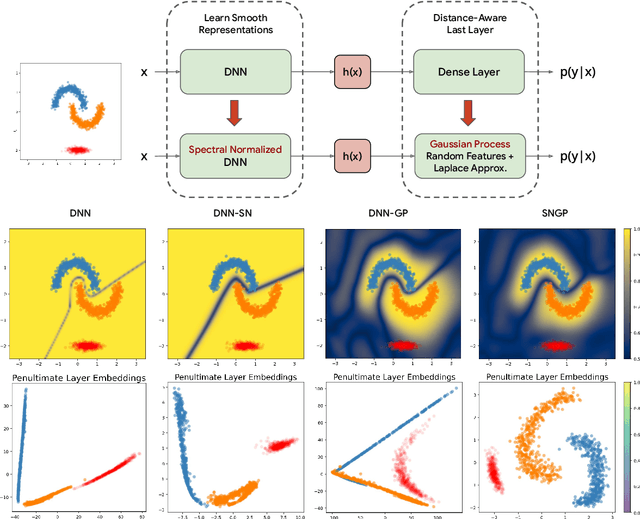
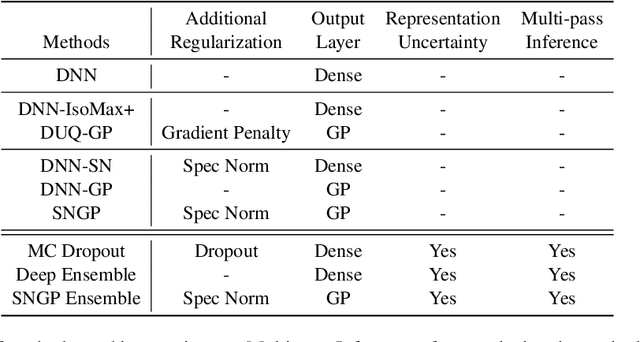
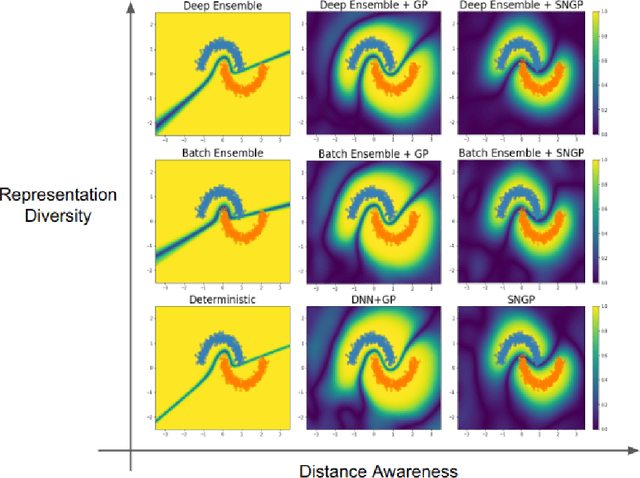
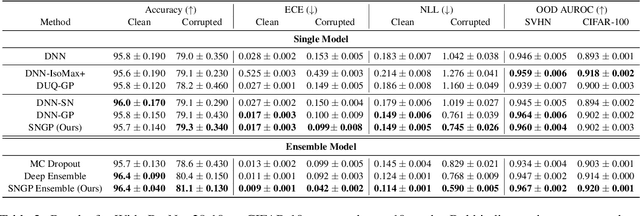
Accurate uncertainty quantification is a major challenge in deep learning, as neural networks can make overconfident errors and assign high confidence predictions to out-of-distribution (OOD) inputs. The most popular approaches to estimate predictive uncertainty in deep learning are methods that combine predictions from multiple neural networks, such as Bayesian neural networks (BNNs) and deep ensembles. However their practicality in real-time, industrial-scale applications are limited due to the high memory and computational cost. Furthermore, ensembles and BNNs do not necessarily fix all the issues with the underlying member networks. In this work, we study principled approaches to improve uncertainty property of a single network, based on a single, deterministic representation. By formalizing the uncertainty quantification as a minimax learning problem, we first identify distance awareness, i.e., the model's ability to quantify the distance of a testing example from the training data, as a necessary condition for a DNN to achieve high-quality (i.e., minimax optimal) uncertainty estimation. We then propose Spectral-normalized Neural Gaussian Process (SNGP), a simple method that improves the distance-awareness ability of modern DNNs with two simple changes: (1) applying spectral normalization to hidden weights to enforce bi-Lipschitz smoothness in representations and (2) replacing the last output layer with a Gaussian process layer. On a suite of vision and language understanding benchmarks, SNGP outperforms other single-model approaches in prediction, calibration and out-of-domain detection. Furthermore, SNGP provides complementary benefits to popular techniques such as deep ensembles and data augmentation, making it a simple and scalable building block for probabilistic deep learning. Code is open-sourced at https://github.com/google/uncertainty-baselines
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge