DEFT: Efficient Finetuning of Conditional Diffusion Models by Learning the Generalised $h$-transform

Generative modelling paradigms based on denoising diffusion processes have emerged as a leading candidate for conditional sampling in inverse problems. In many real-world applications, we often have access to large, expensively trained unconditional diffusion models, which we aim to exploit for improving conditional sampling. Most recent approaches are motivated heuristically and lack a unifying framework, obscuring connections between them. Further, they often suffer from issues such as being very sensitive to hyperparameters, being expensive to train or needing access to weights hidden behind a closed API. In this work, we unify conditional training and sampling using the mathematically well-understood Doob's h-transform. This new perspective allows us to unify many existing methods under a common umbrella. Under this framework, we propose DEFT (Doob's h-transform Efficient FineTuning), a new approach for conditional generation that simply fine-tunes a very small network to quickly learn the conditional $h$-transform, while keeping the larger unconditional network unchanged. DEFT is much faster than existing baselines while achieving state-of-the-art performance across a variety of linear and non-linear benchmarks. On image reconstruction tasks, we achieve speedups of up to 1.6$\times$, while having the best perceptual quality on natural images and reconstruction performance on medical images.

Warm Start Marginal Likelihood Optimisation for Iterative Gaussian Processes

Gaussian processes are a versatile probabilistic machine learning model whose effectiveness often depends on good hyperparameters, which are typically learned by maximising the marginal likelihood. In this work, we consider iterative methods, which use iterative linear system solvers to approximate marginal likelihood gradients up to a specified numerical precision, allowing a trade-off between compute time and accuracy of a solution. We introduce a three-level hierarchy of marginal likelihood optimisation for iterative Gaussian processes, and identify that the computational costs are dominated by solving sequential batches of large positive-definite systems of linear equations. We then propose to amortise computations by reusing solutions of linear system solvers as initialisations in the next step, providing a $\textit{warm start}$. Finally, we discuss the necessary conditions and quantify the consequences of warm starts and demonstrate their effectiveness on regression tasks, where warm starts achieve the same results as the conventional procedure while providing up to a $16 \times$ average speed-up among datasets.

Improving Linear System Solvers for Hyperparameter Optimisation in Iterative Gaussian Processes

Scaling hyperparameter optimisation to very large datasets remains an open problem in the Gaussian process community. This paper focuses on iterative methods, which use linear system solvers, like conjugate gradients, alternating projections or stochastic gradient descent, to construct an estimate of the marginal likelihood gradient. We discuss three key improvements which are applicable across solvers: (i) a pathwise gradient estimator, which reduces the required number of solver iterations and amortises the computational cost of making predictions, (ii) warm starting linear system solvers with the solution from the previous step, which leads to faster solver convergence at the cost of negligible bias, (iii) early stopping linear system solvers after a limited computational budget, which synergises with warm starting, allowing solver progress to accumulate over multiple marginal likelihood steps. These techniques provide speed-ups of up to $72\times$ when solving to tolerance, and decrease the average residual norm by up to $7\times$ when stopping early.

A Generative Model of Symmetry Transformations

Correctly capturing the symmetry transformations of data can lead to efficient models with strong generalization capabilities, though methods incorporating symmetries often require prior knowledge. While recent advancements have been made in learning those symmetries directly from the dataset, most of this work has focused on the discriminative setting. In this paper, we construct a generative model that explicitly aims to capture symmetries in the data, resulting in a model that learns which symmetries are present in an interpretable way. We provide a simple algorithm for efficiently learning our generative model and demonstrate its ability to capture symmetries under affine and color transformations. Combining our symmetry model with existing generative models results in higher marginal test-log-likelihoods and robustness to data sparsification.

Stochastic Gradient Descent for Gaussian Processes Done Right

We study the optimisation problem associated with Gaussian process regression using squared loss. The most common approach to this problem is to apply an exact solver, such as conjugate gradient descent, either directly, or to a reduced-order version of the problem. Recently, driven by successes in deep learning, stochastic gradient descent has gained traction as an alternative. In this paper, we show that when done right$\unicode{x2014}$by which we mean using specific insights from the optimisation and kernel communities$\unicode{x2014}$this approach is highly effective. We thus introduce a particular stochastic dual gradient descent algorithm, that may be implemented with a few lines of code using any deep learning framework. We explain our design decisions by illustrating their advantage against alternatives with ablation studies and show that the new method is highly competitive. Our evaluations on standard regression benchmarks and a Bayesian optimisation task set our approach apart from preconditioned conjugate gradients, variational Gaussian process approximations, and a previous version of stochastic gradient descent for Gaussian processes. On a molecular binding affinity prediction task, our method places Gaussian process regression on par in terms of performance with state-of-the-art graph neural networks.

Sampling from Gaussian Process Posteriors using Stochastic Gradient Descent

Gaussian processes are a powerful framework for quantifying uncertainty and for sequential decision-making but are limited by the requirement of solving linear systems. In general, this has a cubic cost in dataset size and is sensitive to conditioning. We explore stochastic gradient algorithms as a computationally efficient method of approximately solving these linear systems: we develop low-variance optimization objectives for sampling from the posterior and extend these to inducing points. Counterintuitively, stochastic gradient descent often produces accurate predictions, even in cases where it does not converge quickly to the optimum. We explain this through a spectral characterization of the implicit bias from non-convergence. We show that stochastic gradient descent produces predictive distributions close to the true posterior both in regions with sufficient data coverage, and in regions sufficiently far away from the data. Experimentally, stochastic gradient descent achieves state-of-the-art performance on sufficiently large-scale or ill-conditioned regression tasks. Its uncertainty estimates match the performance of significantly more expensive baselines on a large-scale Bayesian~optimization~task.

Kernel Regression with Infinite-Width Neural Networks on Millions of Examples

Neural kernels have drastically increased performance on diverse and nonstandard data modalities but require significantly more compute, which previously limited their application to smaller datasets. In this work, we address this by massively parallelizing their computation across many GPUs. We combine this with a distributed, preconditioned conjugate gradients algorithm to enable kernel regression at a large scale (i.e. up to five million examples). Using this approach, we study scaling laws of several neural kernels across many orders of magnitude for the CIFAR-5m dataset. Using data augmentation to expand the original CIFAR-10 training dataset by a factor of 20, we obtain a test accuracy of 91.2\% (SotA for a pure kernel method). Moreover, we explore neural kernels on other data modalities, obtaining results on protein and small molecule prediction tasks that are competitive with SotA methods.

Sampling-based inference for large linear models, with application to linearised Laplace

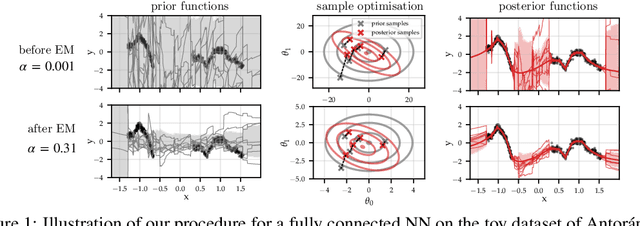
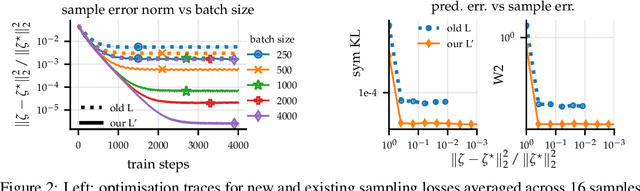
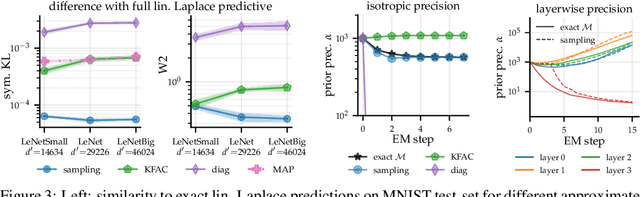
Large-scale linear models are ubiquitous throughout machine learning, with contemporary application as surrogate models for neural network uncertainty quantification; that is, the linearised Laplace method. Alas, the computational cost associated with Bayesian linear models constrains this method's application to small networks, small output spaces and small datasets. We address this limitation by introducing a scalable sample-based Bayesian inference method for conjugate Gaussian multi-output linear models, together with a matching method for hyperparameter (regularisation) selection. Furthermore, we use a classic feature normalisation method (the g-prior) to resolve a previously highlighted pathology of the linearised Laplace method. Together, these contributions allow us to perform linearised neural network inference with ResNet-18 on CIFAR100 (11M parameters, 100 output dimensions x 50k datapoints) and with a U-Net on a high-resolution tomographic reconstruction task (2M parameters, 251k output dimensions).

A Simple Approach to Improve Single-Model Deep Uncertainty via Distance-Awareness

Accurate uncertainty quantification is a major challenge in deep learning, as neural networks can make overconfident errors and assign high confidence predictions to out-of-distribution (OOD) inputs. The most popular approaches to estimate predictive uncertainty in deep learning are methods that combine predictions from multiple neural networks, such as Bayesian neural networks (BNNs) and deep ensembles. However their practicality in real-time, industrial-scale applications are limited due to the high memory and computational cost. Furthermore, ensembles and BNNs do not necessarily fix all the issues with the underlying member networks. In this work, we study principled approaches to improve uncertainty property of a single network, based on a single, deterministic representation. By formalizing the uncertainty quantification as a minimax learning problem, we first identify distance awareness, i.e., the model's ability to quantify the distance of a testing example from the training data, as a necessary condition for a DNN to achieve high-quality (i.e., minimax optimal) uncertainty estimation. We then propose Spectral-normalized Neural Gaussian Process (SNGP), a simple method that improves the distance-awareness ability of modern DNNs with two simple changes: (1) applying spectral normalization to hidden weights to enforce bi-Lipschitz smoothness in representations and (2) replacing the last output layer with a Gaussian process layer. On a suite of vision and language understanding benchmarks, SNGP outperforms other single-model approaches in prediction, calibration and out-of-domain detection. Furthermore, SNGP provides complementary benefits to popular techniques such as deep ensembles and data augmentation, making it a simple and scalable building block for probabilistic deep learning. Code is open-sourced at https://github.com/google/uncertainty-baselines

A Simple Fix to Mahalanobis Distance for Improving Near-OOD Detection

Mahalanobis distance (MD) is a simple and popular post-processing method for detecting out-of-distribution (OOD) inputs in neural networks. We analyze its failure modes for near-OOD detection and propose a simple fix called relative Mahalanobis distance (RMD) which improves performance and is more robust to hyperparameter choice. On a wide selection of challenging vision, language, and biology OOD benchmarks (CIFAR-100 vs CIFAR-10, CLINC OOD intent detection, Genomics OOD), we show that RMD meaningfully improves upon MD performance (by up to 15% AUROC on genomics OOD).