Jihao Andreas Lin
Graph Random Features for Scalable Gaussian Processes
Sep 03, 2025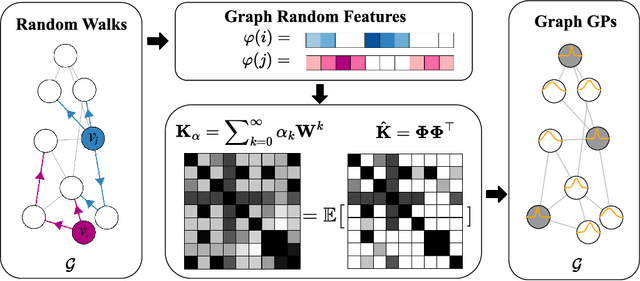

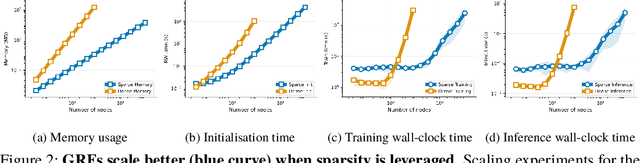

Abstract:We study the application of graph random features (GRFs) - a recently introduced stochastic estimator of graph node kernels - to scalable Gaussian processes on discrete input spaces. We prove that (under mild assumptions) Bayesian inference with GRFs enjoys $O(N^{3/2})$ time complexity with respect to the number of nodes $N$, compared to $O(N^3)$ for exact kernels. Substantial wall-clock speedups and memory savings unlock Bayesian optimisation on graphs with over $10^6$ nodes on a single computer chip, whilst preserving competitive performance.
Successive Halving with Learning Curve Prediction via Latent Kronecker Gaussian Processes
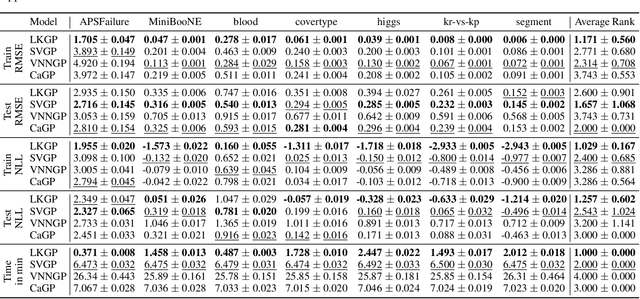
Aug 20, 2025Abstract:Successive Halving is a popular algorithm for hyperparameter optimization which allocates exponentially more resources to promising candidates. However, the algorithm typically relies on intermediate performance values to make resource allocation decisions, which can cause it to prematurely prune slow starters that would eventually become the best candidate. We investigate whether guiding Successive Halving with learning curve predictions based on Latent Kronecker Gaussian Processes can overcome this limitation. In a large-scale empirical study involving different neural network architectures and a click prediction dataset, we compare this predictive approach to the standard approach based on current performance values. Our experiments show that, although the predictive approach achieves competitive performance, it is not Pareto optimal compared to investing more resources into the standard approach, because it requires fully observed learning curves as training data. However, this downside could be mitigated by leveraging existing learning curve data.
Scalable Gaussian Processes: Advances in Iterative Methods and Pathwise Conditioning
Jul 09, 2025Abstract:Gaussian processes are a powerful framework for uncertainty-aware function approximation and sequential decision-making. Unfortunately, their classical formulation does not scale gracefully to large amounts of data and modern hardware for massively-parallel computation, prompting many researchers to develop techniques which improve their scalability. This dissertation focuses on the powerful combination of iterative methods and pathwise conditioning to develop methodological contributions which facilitate the use of Gaussian processes in modern large-scale settings. By combining these two techniques synergistically, expensive computations are expressed as solutions to systems of linear equations and obtained by leveraging iterative linear system solvers. This drastically reduces memory requirements, facilitating application to significantly larger amounts of data, and introduces matrix multiplication as the main computational operation, which is ideal for modern hardware.
Scalable Gaussian Processes with Latent Kronecker Structure
Jun 07, 2025
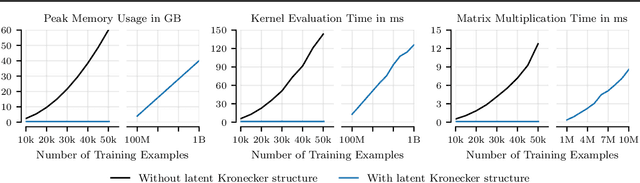
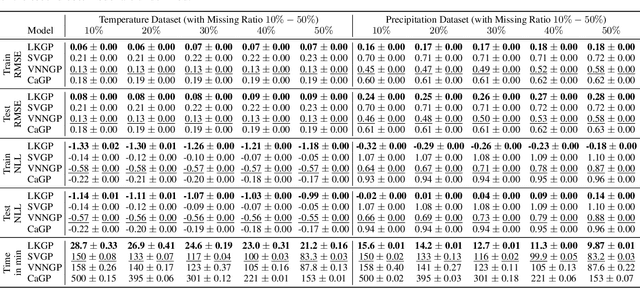
Abstract:Applying Gaussian processes (GPs) to very large datasets remains a challenge due to limited computational scalability. Matrix structures, such as the Kronecker product, can accelerate operations significantly, but their application commonly entails approximations or unrealistic assumptions. In particular, the most common path to creating a Kronecker-structured kernel matrix is by evaluating a product kernel on gridded inputs that can be expressed as a Cartesian product. However, this structure is lost if any observation is missing, breaking the Cartesian product structure, which frequently occurs in real-world data such as time series. To address this limitation, we propose leveraging latent Kronecker structure, by expressing the kernel matrix of observed values as the projection of a latent Kronecker product. In combination with iterative linear system solvers and pathwise conditioning, our method facilitates inference of exact GPs while requiring substantially fewer computational resources than standard iterative methods. We demonstrate that our method outperforms state-of-the-art sparse and variational GPs on real-world datasets with up to five million examples, including robotics, automated machine learning, and climate applications.
Scaling Gaussian Processes for Learning Curve Prediction via Latent Kronecker Structure
Oct 11, 2024



Abstract:A key task in AutoML is to model learning curves of machine learning models jointly as a function of model hyper-parameters and training progression. While Gaussian processes (GPs) are suitable for this task, na\"ive GPs require $\mathcal{O}(n^3m^3)$ time and $\mathcal{O}(n^2 m^2)$ space for $n$ hyper-parameter configurations and $\mathcal{O}(m)$ learning curve observations per hyper-parameter. Efficient inference via Kronecker structure is typically incompatible with early-stopping due to missing learning curve values. We impose $\textit{latent Kronecker structure}$ to leverage efficient product kernels while handling missing values. In particular, we interpret the joint covariance matrix of observed values as the projection of a latent Kronecker product. Combined with iterative linear solvers and structured matrix-vector multiplication, our method only requires $\mathcal{O}(n^3 + m^3)$ time and $\mathcal{O}(n^2 + m^2)$ space. We show that our GP model can match the performance of a Transformer on a learning curve prediction task.
Improving Linear System Solvers for Hyperparameter Optimisation in Iterative Gaussian Processes
May 28, 2024



Abstract:Scaling hyperparameter optimisation to very large datasets remains an open problem in the Gaussian process community. This paper focuses on iterative methods, which use linear system solvers, like conjugate gradients, alternating projections or stochastic gradient descent, to construct an estimate of the marginal likelihood gradient. We discuss three key improvements which are applicable across solvers: (i) a pathwise gradient estimator, which reduces the required number of solver iterations and amortises the computational cost of making predictions, (ii) warm starting linear system solvers with the solution from the previous step, which leads to faster solver convergence at the cost of negligible bias, (iii) early stopping linear system solvers after a limited computational budget, which synergises with warm starting, allowing solver progress to accumulate over multiple marginal likelihood steps. These techniques provide speed-ups of up to $72\times$ when solving to tolerance, and decrease the average residual norm by up to $7\times$ when stopping early.
Warm Start Marginal Likelihood Optimisation for Iterative Gaussian Processes
May 28, 2024



Abstract:Gaussian processes are a versatile probabilistic machine learning model whose effectiveness often depends on good hyperparameters, which are typically learned by maximising the marginal likelihood. In this work, we consider iterative methods, which use iterative linear system solvers to approximate marginal likelihood gradients up to a specified numerical precision, allowing a trade-off between compute time and accuracy of a solution. We introduce a three-level hierarchy of marginal likelihood optimisation for iterative Gaussian processes, and identify that the computational costs are dominated by solving sequential batches of large positive-definite systems of linear equations. We then propose to amortise computations by reusing solutions of linear system solvers as initialisations in the next step, providing a $\textit{warm start}$. Finally, we discuss the necessary conditions and quantify the consequences of warm starts and demonstrate their effectiveness on regression tasks, where warm starts achieve the same results as the conventional procedure while providing up to a $16 \times$ average speed-up among datasets.
Stochastic Gradient Descent for Gaussian Processes Done Right
Oct 31, 2023



Abstract:We study the optimisation problem associated with Gaussian process regression using squared loss. The most common approach to this problem is to apply an exact solver, such as conjugate gradient descent, either directly, or to a reduced-order version of the problem. Recently, driven by successes in deep learning, stochastic gradient descent has gained traction as an alternative. In this paper, we show that when done right$\unicode{x2014}$by which we mean using specific insights from the optimisation and kernel communities$\unicode{x2014}$this approach is highly effective. We thus introduce a particular stochastic dual gradient descent algorithm, that may be implemented with a few lines of code using any deep learning framework. We explain our design decisions by illustrating their advantage against alternatives with ablation studies and show that the new method is highly competitive. Our evaluations on standard regression benchmarks and a Bayesian optimisation task set our approach apart from preconditioned conjugate gradients, variational Gaussian process approximations, and a previous version of stochastic gradient descent for Gaussian processes. On a molecular binding affinity prediction task, our method places Gaussian process regression on par in terms of performance with state-of-the-art graph neural networks.
Beyond Intuition, a Framework for Applying GPs to Real-World Data
Jul 17, 2023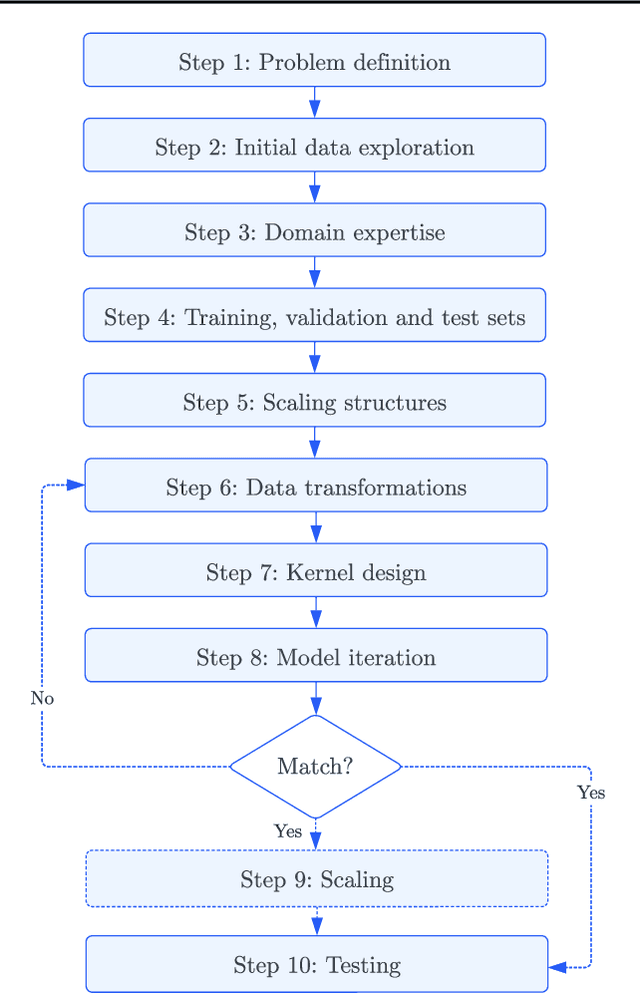
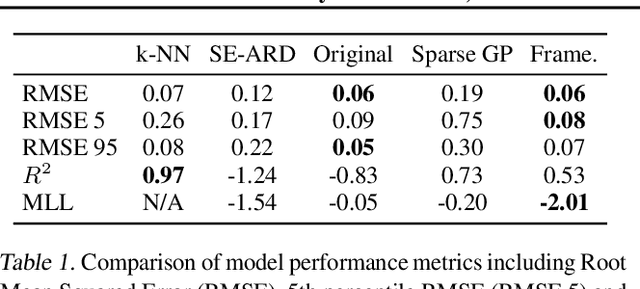
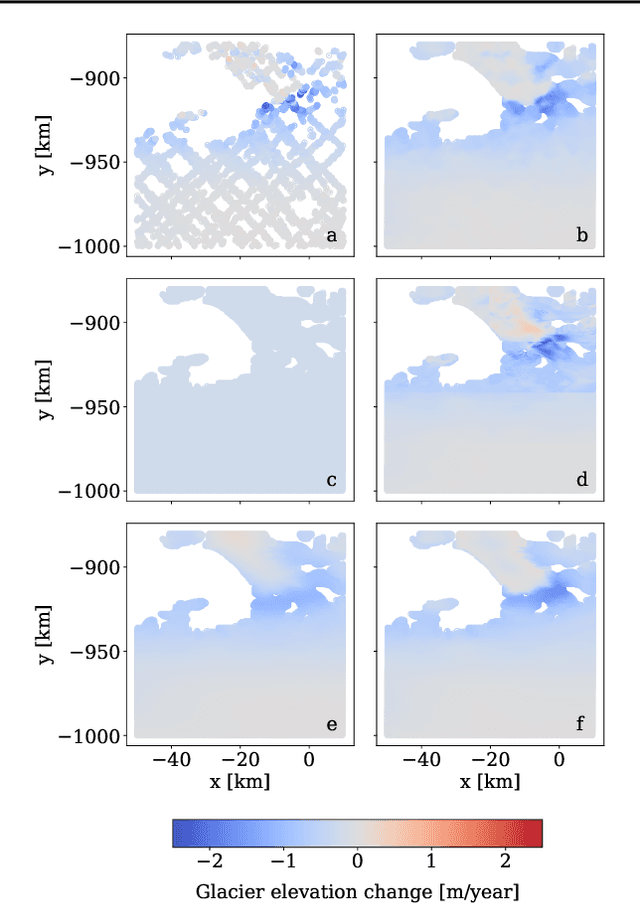
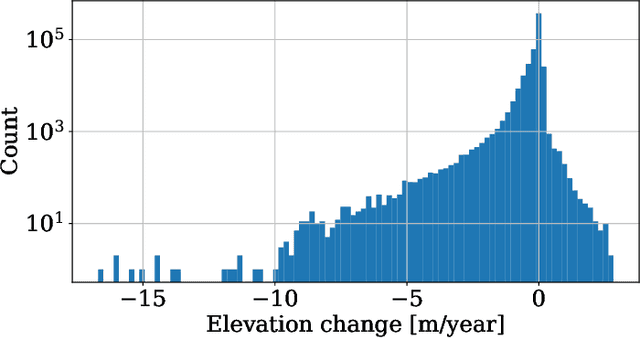
Abstract:Gaussian Processes (GPs) offer an attractive method for regression over small, structured and correlated datasets. However, their deployment is hindered by computational costs and limited guidelines on how to apply GPs beyond simple low-dimensional datasets. We propose a framework to identify the suitability of GPs to a given problem and how to set up a robust and well-specified GP model. The guidelines formalise the decisions of experienced GP practitioners, with an emphasis on kernel design and options for computational scalability. The framework is then applied to a case study of glacier elevation change yielding more accurate results at test time.
Minimal Random Code Learning with Mean-KL Parameterization
Jul 15, 2023Abstract:This paper studies the qualitative behavior and robustness of two variants of Minimal Random Code Learning (MIRACLE) used to compress variational Bayesian neural networks. MIRACLE implements a powerful, conditionally Gaussian variational approximation for the weight posterior $Q_{\mathbf{w}}$ and uses relative entropy coding to compress a weight sample from the posterior using a Gaussian coding distribution $P_{\mathbf{w}}$. To achieve the desired compression rate, $D_{\mathrm{KL}}[Q_{\mathbf{w}} \Vert P_{\mathbf{w}}]$ must be constrained, which requires a computationally expensive annealing procedure under the conventional mean-variance (Mean-Var) parameterization for $Q_{\mathbf{w}}$. Instead, we parameterize $Q_{\mathbf{w}}$ by its mean and KL divergence from $P_{\mathbf{w}}$ to constrain the compression cost to the desired value by construction. We demonstrate that variational training with Mean-KL parameterization converges twice as fast and maintains predictive performance after compression. Furthermore, we show that Mean-KL leads to more meaningful variational distributions with heavier tails and compressed weight samples which are more robust to pruning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge