José Miguel Hernández-Lobato
Scalable Gaussian Processes with Latent Kronecker Structure
Jun 07, 2025
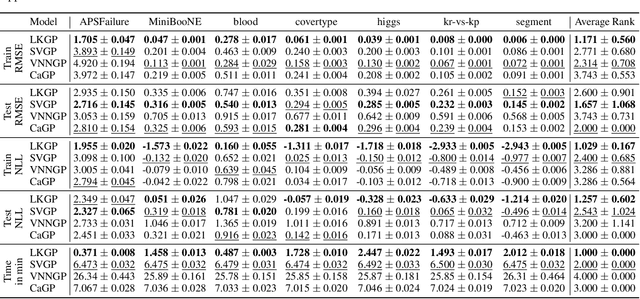
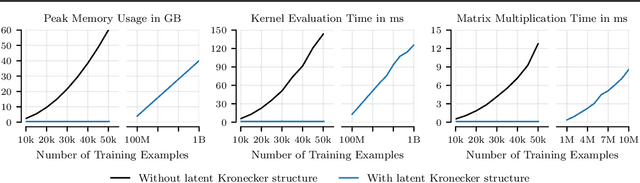
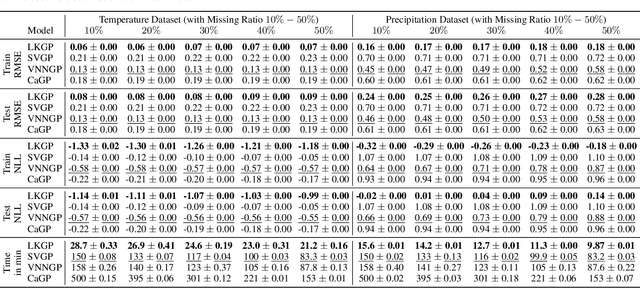
Abstract:Applying Gaussian processes (GPs) to very large datasets remains a challenge due to limited computational scalability. Matrix structures, such as the Kronecker product, can accelerate operations significantly, but their application commonly entails approximations or unrealistic assumptions. In particular, the most common path to creating a Kronecker-structured kernel matrix is by evaluating a product kernel on gridded inputs that can be expressed as a Cartesian product. However, this structure is lost if any observation is missing, breaking the Cartesian product structure, which frequently occurs in real-world data such as time series. To address this limitation, we propose leveraging latent Kronecker structure, by expressing the kernel matrix of observed values as the projection of a latent Kronecker product. In combination with iterative linear system solvers and pathwise conditioning, our method facilitates inference of exact GPs while requiring substantially fewer computational resources than standard iterative methods. We demonstrate that our method outperforms state-of-the-art sparse and variational GPs on real-world datasets with up to five million examples, including robotics, automated machine learning, and climate applications.
RNE: a plug-and-play framework for diffusion density estimation and inference-time control
Jun 06, 2025Abstract:In this paper, we introduce the Radon-Nikodym Estimator (RNE), a flexible, plug-and-play framework for diffusion inference-time density estimation and control, based on the concept of the density ratio between path distributions. RNE connects and unifies a variety of existing density estimation and inference-time control methods under a single and intuitive perspective, stemming from basic variational inference and probabilistic principles therefore offering both theoretical clarity and practical versatility. Experiments demonstrate that RNE achieves promising performances in diffusion density estimation and inference-time control tasks, including annealing, composition of diffusion models, and reward-tilting.
Progressive Tempering Sampler with Diffusion
Jun 05, 2025Abstract:Recent research has focused on designing neural samplers that amortize the process of sampling from unnormalized densities. However, despite significant advancements, they still fall short of the state-of-the-art MCMC approach, Parallel Tempering (PT), when it comes to the efficiency of target evaluations. On the other hand, unlike a well-trained neural sampler, PT yields only dependent samples and needs to be rerun -- at considerable computational cost -- whenever new samples are required. To address these weaknesses, we propose the Progressive Tempering Sampler with Diffusion (PTSD), which trains diffusion models sequentially across temperatures, leveraging the advantages of PT to improve the training of neural samplers. We also introduce a novel method to combine high-temperature diffusion models to generate approximate lower-temperature samples, which are minimally refined using MCMC and used to train the next diffusion model. PTSD enables efficient reuse of sample information across temperature levels while generating well-mixed, uncorrelated samples. Our method significantly improves target evaluation efficiency, outperforming diffusion-based neural samplers.
Aligning Multimodal Representations through an Information Bottleneck
Jun 05, 2025Abstract:Contrastive losses have been extensively used as a tool for multimodal representation learning. However, it has been empirically observed that their use is not effective to learn an aligned representation space. In this paper, we argue that this phenomenon is caused by the presence of modality-specific information in the representation space. Although some of the most widely used contrastive losses maximize the mutual information between representations of both modalities, they are not designed to remove the modality-specific information. We give a theoretical description of this problem through the lens of the Information Bottleneck Principle. We also empirically analyze how different hyperparameters affect the emergence of this phenomenon in a controlled experimental setup. Finally, we propose a regularization term in the loss function that is derived by means of a variational approximation and aims to increase the representational alignment. We analyze in a set of controlled experiments and real-world applications the advantages of including this regularization term.
There Was Never a Bottleneck in Concept Bottleneck Models
Jun 05, 2025Abstract:Deep learning representations are often difficult to interpret, which can hinder their deployment in sensitive applications. Concept Bottleneck Models (CBMs) have emerged as a promising approach to mitigate this issue by learning representations that support target task performance while ensuring that each component predicts a concrete concept from a predefined set. In this work, we argue that CBMs do not impose a true bottleneck: the fact that a component can predict a concept does not guarantee that it encodes only information about that concept. This shortcoming raises concerns regarding interpretability and the validity of intervention procedures. To overcome this limitation, we propose Minimal Concept Bottleneck Models (MCBMs), which incorporate an Information Bottleneck (IB) objective to constrain each representation component to retain only the information relevant to its corresponding concept. This IB is implemented via a variational regularization term added to the training loss. As a result, MCBMs support concept-level interventions with theoretical guarantees, remain consistent with Bayesian principles, and offer greater flexibility in key design choices.
Efficient and Unbiased Sampling from Boltzmann Distributions via Variance-Tuned Diffusion Models
May 27, 2025Abstract:Score-based diffusion models (SBDMs) are powerful amortized samplers for Boltzmann distributions; however, imperfect score estimates bias downstream Monte Carlo estimates. Classical importance sampling (IS) can correct this bias, but computing exact likelihoods requires solving the probability-flow ordinary differential equation (PF-ODE), a procedure that is prohibitively costly and scales poorly with dimensionality. We introduce Variance-Tuned Diffusion Importance Sampling (VT-DIS), a lightweight post-training method that adapts the per-step noise covariance of a pretrained SBDM by minimizing the $\alpha$-divergence ($\alpha=2$) between its forward diffusion and reverse denoising trajectories. VT-DIS assigns a single trajectory-wise importance weight to the joint forward-reverse process, yielding unbiased expectation estimates at test time with negligible overhead compared to standard sampling. On the DW-4, LJ-13, and alanine-dipeptide benchmarks, VT-DIS achieves effective sample sizes of approximately 80 %, 35 %, and 3.5 %, respectively, while using only a fraction of the computational budget required by vanilla diffusion + IS or PF-ODE-based IS.
FEAT: Free energy Estimators with Adaptive Transport
Apr 15, 2025Abstract:We present Free energy Estimators with Adaptive Transport (FEAT), a novel framework for free energy estimation -- a critical challenge across scientific domains. FEAT leverages learned transports implemented via stochastic interpolants and provides consistent, minimum-variance estimators based on escorted Jarzynski equality and controlled Crooks theorem, alongside variational upper and lower bounds on free energy differences. Unifying equilibrium and non-equilibrium methods under a single theoretical framework, FEAT establishes a principled foundation for neural free energy calculations. Experimental validation on toy examples, molecular simulations, and quantum field theory demonstrates improvements over existing learning-based methods.
Causal Effect Estimation under Networked Interference without Networked Unconfoundedness Assumption
Feb 27, 2025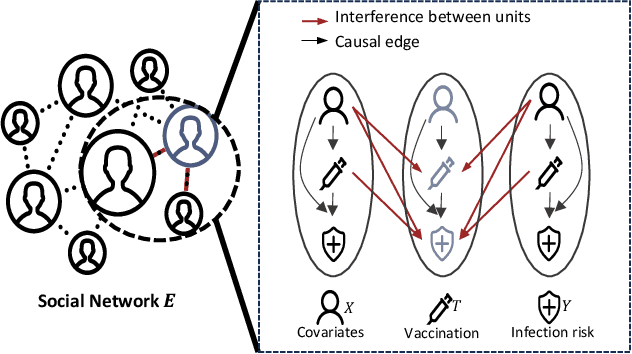
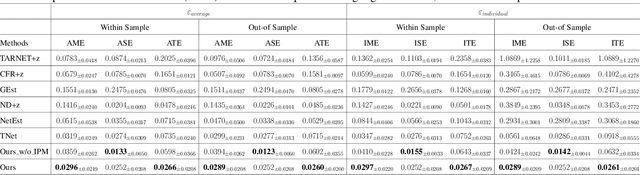
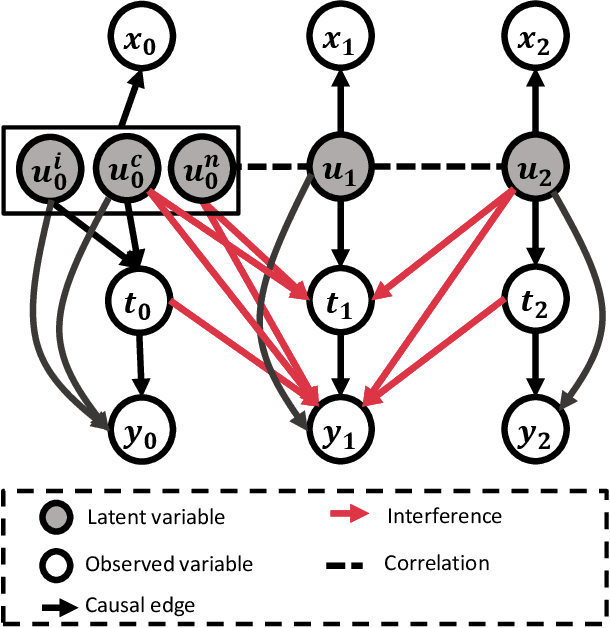
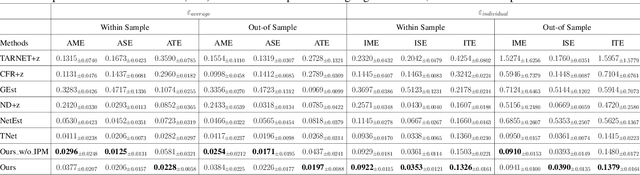
Abstract:Estimating causal effects under networked interference is a crucial yet challenging problem. Existing methods based on observational data mainly rely on the networked unconfoundedness assumption, which guarantees the identification of networked effects. However, the networked unconfoundedness assumption is usually violated due to the latent confounders in observational data, hindering the identification of networked effects. Interestingly, in such networked settings, interactions between units provide valuable information for recovering latent confounders. In this paper, we identify three types of latent confounders in networked inference that hinder identification: those affecting only the individual, those affecting only neighbors, and those influencing both. Specifically, we devise a networked effect estimator based on identifiable representation learning techniques. Theoretically, we establish the identifiability of all latent confounders, and leveraging the identified latent confounders, we provide the networked effect identification result. Extensive experiments validate our theoretical results and demonstrate the effectiveness of the proposed method.
Long-term Causal Inference via Modeling Sequential Latent Confounding
Feb 26, 2025Abstract:Long-term causal inference is an important but challenging problem across various scientific domains. To solve the latent confounding problem in long-term observational studies, existing methods leverage short-term experimental data. Ghassami et al. propose an approach based on the Conditional Additive Equi-Confounding Bias (CAECB) assumption, which asserts that the confounding bias in the short-term outcome is equal to that in the long-term outcome, so that the long-term confounding bias and the causal effects can be identified. While effective in certain cases, this assumption is limited to scenarios with a one-dimensional short-term outcome. In this paper, we introduce a novel assumption that extends the CAECB assumption to accommodate temporal short-term outcomes. Our proposed assumption states a functional relationship between sequential confounding biases across temporal short-term outcomes, under which we theoretically establish the identification of long-term causal effects. Based on the identification result, we develop an estimator and conduct a theoretical analysis of its asymptotic properties. Extensive experiments validate our theoretical results and demonstrate the effectiveness of the proposed method.
Nonparametric Heterogeneous Long-term Causal Effect Estimation via Data Combination
Feb 26, 2025Abstract:Long-term causal inference has drawn increasing attention in many scientific domains. Existing methods mainly focus on estimating average long-term causal effects by combining long-term observational data and short-term experimental data. However, it is still understudied how to robustly and effectively estimate heterogeneous long-term causal effects, significantly limiting practical applications. In this paper, we propose several two-stage style nonparametric estimators for heterogeneous long-term causal effect estimation, including propensity-based, regression-based, and multiple robust estimators. We conduct a comprehensive theoretical analysis of their asymptotic properties under mild assumptions, with the ultimate goal of building a better understanding of the conditions under which some estimators can be expected to perform better. Extensive experiments across several semi-synthetic and real-world datasets validate the theoretical results and demonstrate the effectiveness of the proposed estimators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge