On the design space between molecular mechanics and machine learning force fields

A force field as accurate as quantum mechanics (QM) and as fast as molecular mechanics (MM), with which one can simulate a biomolecular system efficiently enough and meaningfully enough to get quantitative insights, is among the most ardent dreams of biophysicists -- a dream, nevertheless, not to be fulfilled any time soon. Machine learning force fields (MLFFs) represent a meaningful endeavor towards this direction, where differentiable neural functions are parametrized to fit ab initio energies, and furthermore forces through automatic differentiation. We argue that, as of now, the utility of the MLFF models is no longer bottlenecked by accuracy but primarily by their speed (as well as stability and generalizability), as many recent variants, on limited chemical spaces, have long surpassed the chemical accuracy of $1$ kcal/mol -- the empirical threshold beyond which realistic chemical predictions are possible -- though still magnitudes slower than MM. Hoping to kindle explorations and designs of faster, albeit perhaps slightly less accurate MLFFs, in this review, we focus our attention on the design space (the speed-accuracy tradeoff) between MM and ML force fields. After a brief review of the building blocks of force fields of either kind, we discuss the desired properties and challenges now faced by the force field development community, survey the efforts to make MM force fields more accurate and ML force fields faster, envision what the next generation of MLFF might look like.

Harnessing Earnings Reports for Stock Predictions: A QLoRA-Enhanced LLM Approach

Accurate stock market predictions following earnings reports are crucial for investors. Traditional methods, particularly classical machine learning models, struggle with these predictions because they cannot effectively process and interpret extensive textual data contained in earnings reports and often overlook nuances that influence market movements. This paper introduces an advanced approach by employing Large Language Models (LLMs) instruction fine-tuned with a novel combination of instruction-based techniques and quantized low-rank adaptation (QLoRA) compression. Our methodology integrates 'base factors', such as financial metric growth and earnings transcripts, with 'external factors', including recent market indices performances and analyst grades, to create a rich, supervised dataset. This comprehensive dataset enables our models to achieve superior predictive performance in terms of accuracy, weighted F1, and Matthews correlation coefficient (MCC), especially evident in the comparison with benchmarks such as GPT-4. We specifically highlight the efficacy of the llama-3-8b-Instruct-4bit model, which showcases significant improvements over baseline models. The paper also discusses the potential of expanding the output capabilities to include a 'Hold' option and extending the prediction horizon, aiming to accommodate various investment styles and time frames. This study not only demonstrates the power of integrating cutting-edge AI with fine-tuned financial data but also paves the way for future research in enhancing AI-driven financial analysis tools.

Non-convolutional Graph Neural Networks

Rethink convolution-based graph neural networks (GNN) -- they characteristically suffer from limited expressiveness, over-smoothing, and over-squashing, and require specialized sparse kernels for efficient computation. Here, we design a simple graph learning module entirely free of convolution operators, coined random walk with unifying memory (RUM) neural network, where an RNN merges the topological and semantic graph features along the random walks terminating at each node. Relating the rich literature on RNN behavior and graph topology, we theoretically show and experimentally verify that RUM attenuates the aforementioned symptoms and is more expressive than the Weisfeiler-Lehman (WL) isomorphism test. On a variety of node- and graph-level classification and regression tasks, RUM not only achieves competitive performance, but is also robust, memory-efficient, scalable, and faster than the simplest convolutional GNNs.

Espaloma-0.3.0: Machine-learned molecular mechanics force field for the simulation of protein-ligand systems and beyond

Molecular mechanics (MM) force fields -- the models that characterize the energy landscape of molecular systems via simple pairwise and polynomial terms -- have traditionally relied on human expert-curated, inflexible, and poorly extensible discrete chemical parameter assignment rules, namely atom or valence types. Recently, there has been significant interest in using graph neural networks to replace this process, while enabling the parametrization scheme to be learned in an end-to-end differentiable manner directly from quantum chemical calculations or condensed-phase data. In this paper, we extend the Espaloma end-to-end differentiable force field construction approach by incorporating both energy and force fitting directly to quantum chemical data into the training process. Building on the OpenMM SPICE dataset, we curate a dataset containing chemical spaces highly relevant to the broad interest of biomolecular modeling, covering small molecules, proteins, and RNA. The resulting force field, espaloma 0.3.0, self-consistently parametrizes these diverse biomolecular species, accurately predicts quantum chemical energies and forces, and maintains stable quantum chemical energy-minimized geometries. Surprisingly, this simple approach produces highly accurate protein-ligand binding free energies when self-consistently parametrizing protein and ligand. This approach -- capable of fitting new force fields to large quantum chemical datasets in one GPU-day -- shows significant promise as a path forward for building systematically more accurate force fields that can be easily extended to new chemical domains of interest.

EspalomaCharge: Machine learning-enabled ultra-fast partial charge assignment

Atomic partial charges are crucial parameters in molecular dynamics (MD) simulation, dictating the electrostatic contributions to intermolecular energies, and thereby the potential energy landscape. Traditionally, the assignment of partial charges has relied on surrogates of \textit{ab initio} semiempirical quantum chemical methods such as AM1-BCC, and is expensive for large systems or large numbers of molecules. We propose a hybrid physical / graph neural network-based approximation to the widely popular AM1-BCC charge model that is orders of magnitude faster while maintaining accuracy comparable to differences in AM1-BCC implementations. Our hybrid approach couples a graph neural network to a streamlined charge equilibration approach in order to predict molecule-specific atomic electronegativity and hardness parameters, followed by analytical determination of optimal charge-equilibrated parameters that preserves total molecular charge. This hybrid approach scales linearly with the number of atoms, enabling, for the first time, the use of fully consistent charge models for small molecules and biopolymers for the construction of next-generation self-consistent biomolecular force fields. Implemented in the free and open source package \texttt{espaloma\_charge}, this approach provides drop-in replacements for both AmberTools \texttt{antechamber} and the Open Force Field Toolkit charging workflows, in addition to stand-alone charge generation interfaces. Source code is available at \url{https://github.com/choderalab/espaloma_charge}.

Spatial Attention Kinetic Networks with E(n)-Equivariance

Neural networks that are equivariant to rotations, translations, reflections, and permutations on n-dimensional geometric space have shown promise in physical modeling for tasks such as accurately but inexpensively modeling complex potential energy surfaces to guiding the sampling of complex dynamical systems or forecasting their time evolution. Current state-of-the-art methods employ spherical harmonics to encode higher-order interactions among particles, which are computationally expensive. In this paper, we propose a simple alternative functional form that uses neurally parametrized linear combinations of edge vectors to achieve equivariance while still universally approximating node environments. Incorporating this insight, we design spatial attention kinetic networks with E(n)-equivariance, or SAKE, which are competitive in many-body system modeling tasks while being significantly faster.

SPICE, A Dataset of Drug-like Molecules and Peptides for Training Machine Learning Potentials

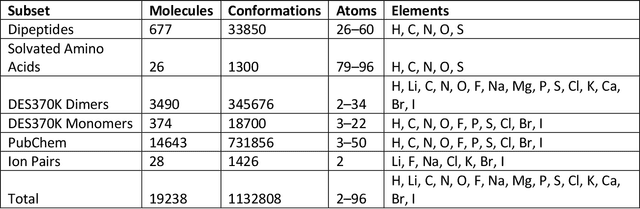
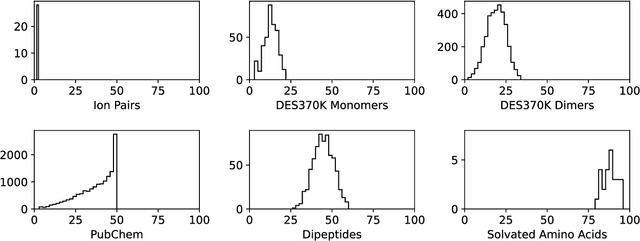
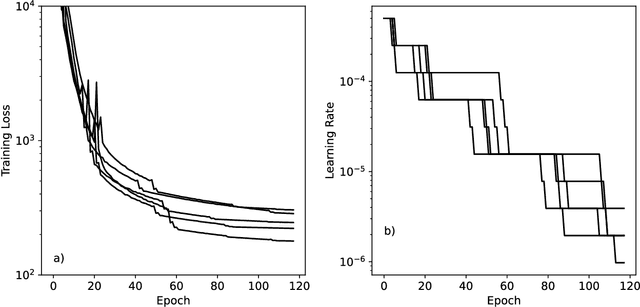
Machine learning potentials are an important tool for molecular simulation, but their development is held back by a shortage of high quality datasets to train them on. We describe the SPICE dataset, a new quantum chemistry dataset for training potentials relevant to simulating drug-like small molecules interacting with proteins. It contains over 1.1 million conformations for a diverse set of small molecules, dimers, dipeptides, and solvated amino acids. It includes 15 elements, charged and uncharged molecules, and a wide range of covalent and non-covalent interactions. It provides both forces and energies calculated at the {\omega}B97M-D3(BJ)/def2-TZVPPD level of theory, along with other useful quantities such as multipole moments and bond orders. We train a set of machine learning potentials on it and demonstrate that they can achieve chemical accuracy across a broad region of chemical space. It can serve as a valuable resource for the creation of transferable, ready to use potential functions for use in molecular simulations.

Stochastic Aggregation in Graph Neural Networks

Graph neural networks (GNNs) manifest pathologies including over-smoothing and limited discriminating power as a result of suboptimally expressive aggregating mechanisms. We herein present a unifying framework for stochastic aggregation (STAG) in GNNs, where noise is (adaptively) injected into the aggregation process from the neighborhood to form node embeddings. We provide theoretical arguments that STAG models, with little overhead, remedy both of the aforementioned problems. In addition to fixed-noise models, we also propose probabilistic versions of STAG models and a variational inference framework to learn the noise posterior. We conduct illustrative experiments clearly targeting oversmoothing and multiset aggregation limitations. Furthermore, STAG enhances general performance of GNNs demonstrated by competitive performance in common citation and molecule graph benchmark datasets.

End-to-End Differentiable Molecular Mechanics Force Field Construction

Molecular mechanics (MM) potentials have long been a workhorse of computational chemistry. Leveraging accuracy and speed, these functional forms find use in a wide variety of applications from rapid virtual screening to detailed free energy calculations. Traditionally, MM potentials have relied on human-curated, inflexible, and poorly extensible discrete chemical perception rules (atom types) for applying parameters to molecules or biopolymers, making them difficult to optimize to fit quantum chemical or physical property data. Here, we propose an alternative approach that uses graph nets to perceive chemical environments, producing continuous atom embeddings from which valence and nonbonded parameters can be predicted using a feed-forward neural network. Since all stages are built using smooth functions, the entire process of chemical perception and parameter assignment is differentiable end-to-end with respect to model parameters, allowing new force fields to be easily constructed, extended, and applied to arbitrary molecules. We show that this approach has the capacity to reproduce legacy atom types and can be fit to MM and QM energies and forces, among other targets.

Graph Nets for Partial Charge Prediction

Atomic partial charges are crucial parameters for Molecular Dynamics (MD) simulations, molecular mechanics calculations, and virtual screening, as they determine the electrostatic contributions to interaction energies. Current methods for calculating partial charges, however, are either slow and scale poorly with molecular size (quantum chemical methods) or unreliable (empirical methods). Here, we present a new charge derivation method based on Graph Nets---a set of update and aggregate functions that operate on molecular topologies and propagate information thereon---that could approximate charges derived from Density Functional Theory (DFT) calculations with high accuracy and an over 500-fold speed up.