Causal-aware Large Language Models: Enhancing Decision-Making Through Learning, Adapting and Acting

Large language models (LLMs) have shown great potential in decision-making due to the vast amount of knowledge stored within the models. However, these pre-trained models are prone to lack reasoning abilities and are difficult to adapt to new environments, further hindering their application to complex real-world tasks. To address these challenges, inspired by the human cognitive process, we propose Causal-aware LLMs, which integrate the structural causal model (SCM) into the decision-making process to model, update, and utilize structured knowledge of the environment in a ``learning-adapting-acting" paradigm. Specifically, in the learning stage, we first utilize an LLM to extract the environment-specific causal entities and their causal relations to initialize a structured causal model of the environment. Subsequently,in the adapting stage, we update the structured causal model through external feedback about the environment, via an idea of causal intervention. Finally, in the acting stage, Causal-aware LLMs exploit structured causal knowledge for more efficient policy-making through the reinforcement learning agent. The above processes are performed iteratively to learn causal knowledge, ultimately enabling the causal-aware LLMs to achieve a more accurate understanding of the environment and make more efficient decisions. Experimental results across 22 diverse tasks within the open-world game ``Crafter" validate the effectiveness of our proposed method.

An Identifiable Cost-Aware Causal Decision-Making Framework Using Counterfactual Reasoning

Decision making under abnormal conditions is a critical process that involves evaluating the current state and determining the optimal action to restore the system to a normal state at an acceptable cost. However, in such scenarios, existing decision-making frameworks highly rely on reinforcement learning or root cause analysis, resulting in them frequently neglecting the cost of the actions or failing to incorporate causal mechanisms adequately. By relaxing the existing causal decision framework to solve the necessary cause, we propose a minimum-cost causal decision (MiCCD) framework via counterfactual reasoning to address the above challenges. Emphasis is placed on making counterfactual reasoning processes identifiable in the presence of a large amount of mixed anomaly data, as well as finding the optimal intervention state in a continuous decision space. Specifically, it formulates a surrogate model based on causal graphs, using abnormal pattern clustering labels as supervisory signals. This enables the approximation of the structural causal model among the variables and lays a foundation for identifiable counterfactual reasoning. With the causal structure approximated, we then established an optimization model based on counterfactual estimation. The Sequential Least Squares Programming (SLSQP) algorithm is further employed to optimize intervention strategies while taking costs into account. Experimental evaluations on both synthetic and real-world datasets reveal that MiCCD outperforms conventional methods across multiple metrics, including F1-score, cost efficiency, and ranking quality(nDCG@k values), thus validating its efficacy and broad applicability.

Causal View of Time Series Imputation: Some Identification Results on Missing Mechanism

Time series imputation is one of the most challenge problems and has broad applications in various fields like health care and the Internet of Things. Existing methods mainly aim to model the temporally latent dependencies and the generation process from the observed time series data. In real-world scenarios, different types of missing mechanisms, like MAR (Missing At Random), and MNAR (Missing Not At Random) can occur in time series data. However, existing methods often overlook the difference among the aforementioned missing mechanisms and use a single model for time series imputation, which can easily lead to misleading results due to mechanism mismatching. In this paper, we propose a framework for time series imputation problem by exploring Different Missing Mechanisms (DMM in short) and tailoring solutions accordingly. Specifically, we first analyze the data generation processes with temporal latent states and missing cause variables for different mechanisms. Sequentially, we model these generation processes via variational inference and estimate prior distributions of latent variables via normalizing flow-based neural architecture. Furthermore, we establish identifiability results under the nonlinear independent component analysis framework to show that latent variables are identifiable. Experimental results show that our method surpasses existing time series imputation techniques across various datasets with different missing mechanisms, demonstrating its effectiveness in real-world applications.

Long-Term Individual Causal Effect Estimation via Identifiable Latent Representation Learning

Estimating long-term causal effects by combining long-term observational and short-term experimental data is a crucial but challenging problem in many real-world scenarios. In existing methods, several ideal assumptions, e.g. latent unconfoundedness assumption or additive equi-confounding bias assumption, are proposed to address the latent confounder problem raised by the observational data. However, in real-world applications, these assumptions are typically violated which limits their practical effectiveness. In this paper, we tackle the problem of estimating the long-term individual causal effects without the aforementioned assumptions. Specifically, we propose to utilize the natural heterogeneity of data, such as data from multiple sources, to identify latent confounders, thereby significantly avoiding reliance on idealized assumptions. Practically, we devise a latent representation learning-based estimator of long-term causal effects. Theoretically, we establish the identifiability of latent confounders, with which we further achieve long-term effect identification. Extensive experimental studies, conducted on multiple synthetic and semi-synthetic datasets, demonstrate the effectiveness of our proposed method.

Interpretable High-order Knowledge Graph Neural Network for Predicting Synthetic Lethality in Human Cancers

Synthetic lethality (SL) is a promising gene interaction for cancer therapy. Recent SL prediction methods integrate knowledge graphs (KGs) into graph neural networks (GNNs) and employ attention mechanisms to extract local subgraphs as explanations for target gene pairs. However, attention mechanisms often lack fidelity, typically generate a single explanation per gene pair, and fail to ensure trustworthy high-order structures in their explanations. To overcome these limitations, we propose Diverse Graph Information Bottleneck for Synthetic Lethality (DGIB4SL), a KG-based GNN that generates multiple faithful explanations for the same gene pair and effectively encodes high-order structures. Specifically, we introduce a novel DGIB objective, integrating a Determinant Point Process (DPP) constraint into the standard IB objective, and employ 13 motif-based adjacency matrices to capture high-order structures in gene representations. Experimental results show that DGIB4SL outperforms state-of-the-art baselines and provides multiple explanations for SL prediction, revealing diverse biological mechanisms underlying SL inference.

Causal Effect Estimation under Networked Interference without Networked Unconfoundedness Assumption

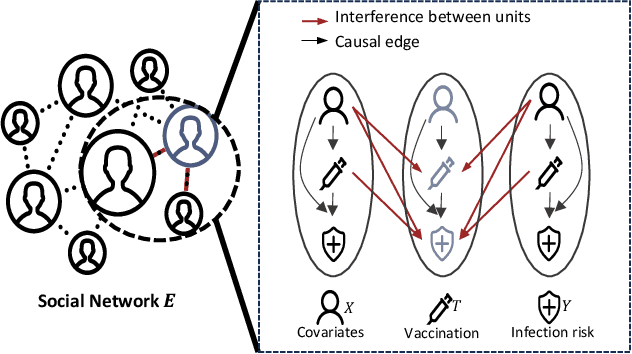
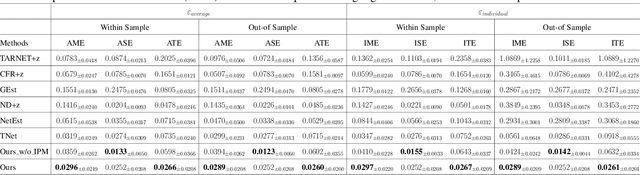
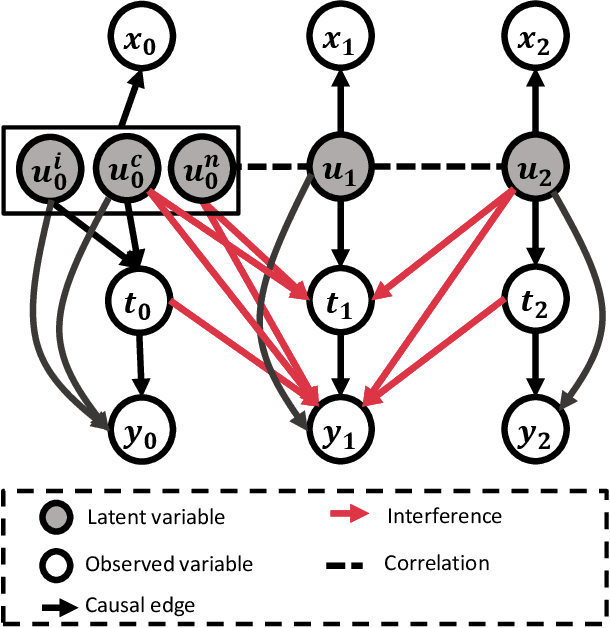
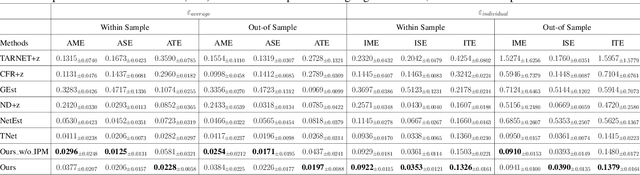
Estimating causal effects under networked interference is a crucial yet challenging problem. Existing methods based on observational data mainly rely on the networked unconfoundedness assumption, which guarantees the identification of networked effects. However, the networked unconfoundedness assumption is usually violated due to the latent confounders in observational data, hindering the identification of networked effects. Interestingly, in such networked settings, interactions between units provide valuable information for recovering latent confounders. In this paper, we identify three types of latent confounders in networked inference that hinder identification: those affecting only the individual, those affecting only neighbors, and those influencing both. Specifically, we devise a networked effect estimator based on identifiable representation learning techniques. Theoretically, we establish the identifiability of all latent confounders, and leveraging the identified latent confounders, we provide the networked effect identification result. Extensive experiments validate our theoretical results and demonstrate the effectiveness of the proposed method.

Long-term Causal Inference via Modeling Sequential Latent Confounding

Long-term causal inference is an important but challenging problem across various scientific domains. To solve the latent confounding problem in long-term observational studies, existing methods leverage short-term experimental data. Ghassami et al. propose an approach based on the Conditional Additive Equi-Confounding Bias (CAECB) assumption, which asserts that the confounding bias in the short-term outcome is equal to that in the long-term outcome, so that the long-term confounding bias and the causal effects can be identified. While effective in certain cases, this assumption is limited to scenarios with a one-dimensional short-term outcome. In this paper, we introduce a novel assumption that extends the CAECB assumption to accommodate temporal short-term outcomes. Our proposed assumption states a functional relationship between sequential confounding biases across temporal short-term outcomes, under which we theoretically establish the identification of long-term causal effects. Based on the identification result, we develop an estimator and conduct a theoretical analysis of its asymptotic properties. Extensive experiments validate our theoretical results and demonstrate the effectiveness of the proposed method.

Nonparametric Heterogeneous Long-term Causal Effect Estimation via Data Combination

Long-term causal inference has drawn increasing attention in many scientific domains. Existing methods mainly focus on estimating average long-term causal effects by combining long-term observational data and short-term experimental data. However, it is still understudied how to robustly and effectively estimate heterogeneous long-term causal effects, significantly limiting practical applications. In this paper, we propose several two-stage style nonparametric estimators for heterogeneous long-term causal effect estimation, including propensity-based, regression-based, and multiple robust estimators. We conduct a comprehensive theoretical analysis of their asymptotic properties under mild assumptions, with the ultimate goal of building a better understanding of the conditions under which some estimators can be expected to perform better. Extensive experiments across several semi-synthetic and real-world datasets validate the theoretical results and demonstrate the effectiveness of the proposed estimators.

Time Series Domain Adaptation via Latent Invariant Causal Mechanism

Time series domain adaptation aims to transfer the complex temporal dependence from the labeled source domain to the unlabeled target domain. Recent advances leverage the stable causal mechanism over observed variables to model the domain-invariant temporal dependence. However, modeling precise causal structures in high-dimensional data, such as videos, remains challenging. Additionally, direct causal edges may not exist among observed variables (e.g., pixels). These limitations hinder the applicability of existing approaches to real-world scenarios. To address these challenges, we find that the high-dimension time series data are generated from the low-dimension latent variables, which motivates us to model the causal mechanisms of the temporal latent process. Based on this intuition, we propose a latent causal mechanism identification framework that guarantees the uniqueness of the reconstructed latent causal structures. Specifically, we first identify latent variables by utilizing sufficient changes in historical information. Moreover, by enforcing the sparsity of the relationships of latent variables, we can achieve identifiable latent causal structures. Built on the theoretical results, we develop the Latent Causality Alignment (LCA) model that leverages variational inference, which incorporates an intra-domain latent sparsity constraint for latent structure reconstruction and an inter-domain latent sparsity constraint for domain-invariant structure reconstruction. Experiment results on eight benchmarks show a general improvement in the domain-adaptive time series classification and forecasting tasks, highlighting the effectiveness of our method in real-world scenarios. Codes are available at https://github.com/DMIRLAB-Group/LCA.

Disentangling Long-Short Term State Under Unknown Interventions for Online Time Series Forecasting

Current methods for time series forecasting struggle in the online scenario, since it is difficult to preserve long-term dependency while adapting short-term changes when data are arriving sequentially. Although some recent methods solve this problem by controlling the updates of latent states, they cannot disentangle the long/short-term states, leading to the inability to effectively adapt to nonstationary. To tackle this challenge, we propose a general framework to disentangle long/short-term states for online time series forecasting. Our idea is inspired by the observations where short-term changes can be led by unknown interventions like abrupt policies in the stock market. Based on this insight, we formalize a data generation process with unknown interventions on short-term states. Under mild assumptions, we further leverage the independence of short-term states led by unknown interventions to establish the identification theory to achieve the disentanglement of long/short-term states. Built on this theory, we develop a long short-term disentanglement model (LSTD) to extract the long/short-term states with long/short-term encoders, respectively. Furthermore, the LSTD model incorporates a smooth constraint to preserve the long-term dependencies and an interrupted dependency constraint to enforce the forgetting of short-term dependencies, together boosting the disentanglement of long/short-term states. Experimental results on several benchmark datasets show that our \textbf{LSTD} model outperforms existing methods for online time series forecasting, validating its efficacy in real-world applications.