Refined climatologies of future precipitation over High Mountain Asia using probabilistic ensemble learning

High Mountain Asia holds the largest concentration of frozen water outside the polar regions, serving as a crucial water source for more than 1.9 billion people. In the face of climate change, precipitation represents the largest source of uncertainty for hydrological modelling in this area. Future precipitation predictions remain challenging due to complex orography, lack of in situ hydrological observations, and limitations in climate model resolution and parametrisation for this region. To address the uncertainty posed by these challenges, climate models are often aggregated into multi-model ensembles. While multi-model ensembles are known to improve the predictive accuracy and analysis of future climate projections, consensus regarding how models are aggregated is lacking. In this study, we propose a probabilistic machine learning framework to systematically combine 13 regional climate models from the Coordinated Regional Downscaling Experiment (CORDEX) over High Mountain Asia. Our approach accounts for seasonal and spatial biases within the models, enabling the prediction of more faithful precipitation distributions. The framework is validated against gridded historical precipitation data and is used to generate projections for the near-future (2036-2065) and far-future (2066-2095) under RCP4.5 and RCP8.5 scenarios.

Beyond Intuition, a Framework for Applying GPs to Real-World Data

Gaussian Processes (GPs) offer an attractive method for regression over small, structured and correlated datasets. However, their deployment is hindered by computational costs and limited guidelines on how to apply GPs beyond simple low-dimensional datasets. We propose a framework to identify the suitability of GPs to a given problem and how to set up a robust and well-specified GP model. The guidelines formalise the decisions of experienced GP practitioners, with an emphasis on kernel design and options for computational scalability. The framework is then applied to a case study of glacier elevation change yielding more accurate results at test time.

Pyrocast: a Machine Learning Pipeline to Forecast Pyrocumulonimbus (PyroCb) Clouds

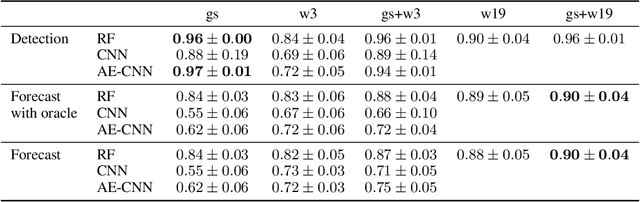
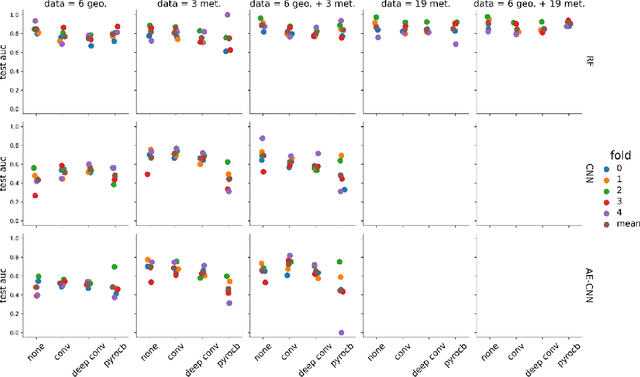
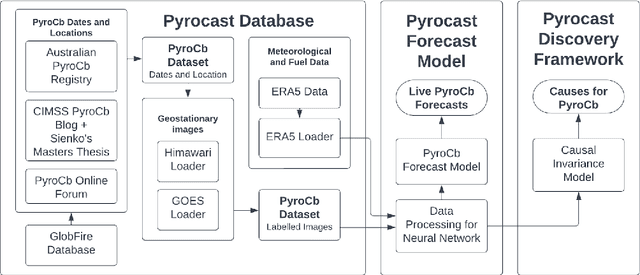
Pyrocumulonimbus (pyroCb) clouds are storm clouds generated by extreme wildfires. PyroCbs are associated with unpredictable, and therefore dangerous, wildfire spread. They can also inject smoke particles and trace gases into the upper troposphere and lower stratosphere, affecting the Earth's climate. As global temperatures increase, these previously rare events are becoming more common. Being able to predict which fires are likely to generate pyroCb is therefore key to climate adaptation in wildfire-prone areas. This paper introduces Pyrocast, a pipeline for pyroCb analysis and forecasting. The pipeline's first two components, a pyroCb database and a pyroCb forecast model, are presented. The database brings together geostationary imagery and environmental data for over 148 pyroCb events across North America, Australia, and Russia between 2018 and 2022. Random Forests, Convolutional Neural Networks (CNNs), and CNNs pretrained with Auto-Encoders were tested to predict the generation of pyroCb for a given fire six hours in advance. The best model predicted pyroCb with an AUC of $0.90 \pm 0.04$.

Identifying the Causes of Pyrocumulonimbus (PyroCb)

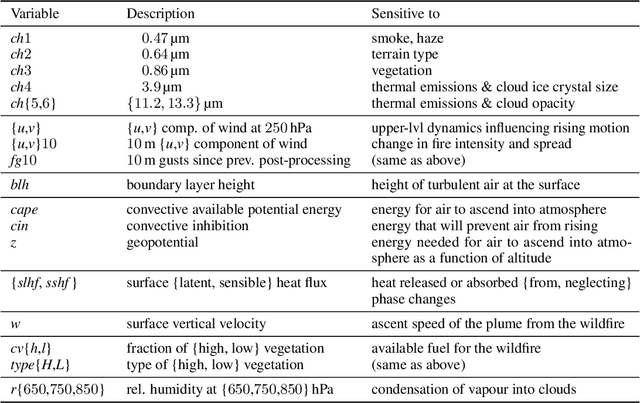
A first causal discovery analysis from observational data of pyroCb (storm clouds generated from extreme wildfires) is presented. Invariant Causal Prediction was used to develop tools to understand the causal drivers of pyroCb formation. This includes a conditional independence test for testing $Y$ conditionally independent of $E$ given $X$ for binary variable $Y$ and multivariate, continuous variables $X$ and $E$, and a greedy-ICP search algorithm that relies on fewer conditional independence tests to obtain a smaller more manageable set of causal predictors. With these tools, we identified a subset of seven causal predictors which are plausible when contrasted with domain knowledge: surface sensible heat flux, relative humidity at $850$ hPa, a component of wind at $250$ hPa, $13.3$ micro-meters, thermal emissions, convective available potential energy, and altitude.

Kernel Learning for Explainable Climate Science

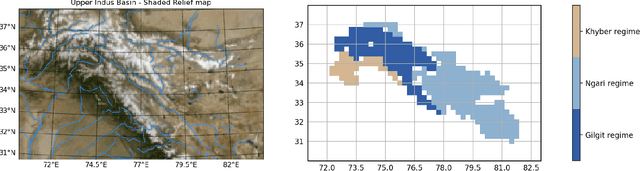
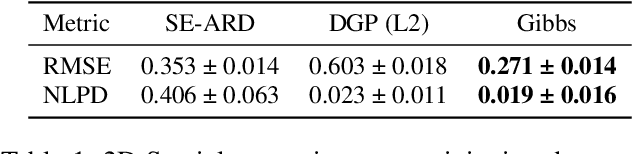
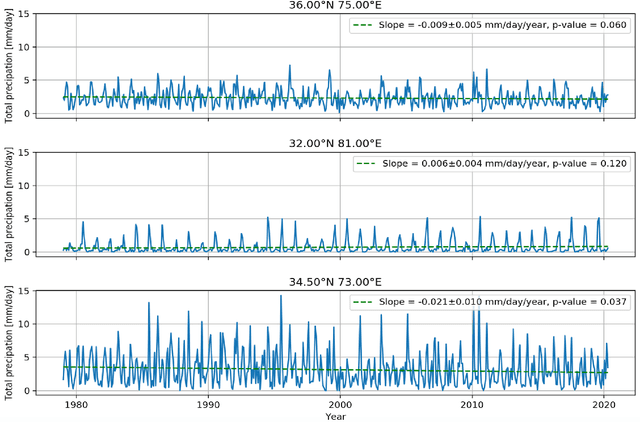
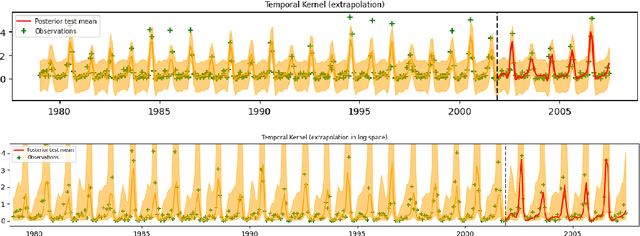
The Upper Indus Basin, Himalayas provides water for 270 million people and countless ecosystems. However, precipitation, a key component to hydrological modelling, is poorly understood in this area. A key challenge surrounding this uncertainty comes from the complex spatial-temporal distribution of precipitation across the basin. In this work we propose Gaussian processes with structured non-stationary kernels to model precipitation patterns in the UIB. Previous attempts to quantify or model precipitation in the Hindu Kush Karakoram Himalayan region have often been qualitative or include crude assumptions and simplifications which cannot be resolved at lower resolutions. This body of research also provides little to no error propagation. We account for the spatial variation in precipitation with a non-stationary Gibbs kernel parameterised with an input dependent lengthscale. This allows the posterior function samples to adapt to the varying precipitation patterns inherent in the distinct underlying topography of the Indus region. The input dependent lengthscale is governed by a latent Gaussian process with a stationary squared-exponential kernel to allow the function level hyperparameters to vary smoothly. In ablation experiments we motivate each component of the proposed kernel by demonstrating its ability to model the spatial covariance, temporal structure and joint spatio-temporal reconstruction. We benchmark our model with a stationary Gaussian process and a Deep Gaussian processes.