Training Language Models on the Knowledge Graph: Insights on Hallucinations and Their Detectability

While many capabilities of language models (LMs) improve with increased training budget, the influence of scale on hallucinations is not yet fully understood. Hallucinations come in many forms, and there is no universally accepted definition. We thus focus on studying only those hallucinations where a correct answer appears verbatim in the training set. To fully control the training data content, we construct a knowledge graph (KG)-based dataset, and use it to train a set of increasingly large LMs. We find that for a fixed dataset, larger and longer-trained LMs hallucinate less. However, hallucinating on $\leq5$% of the training data requires an order of magnitude larger model, and thus an order of magnitude more compute, than Hoffmann et al. (2022) reported was optimal. Given this costliness, we study how hallucination detectors depend on scale. While we see detector size improves performance on fixed LM's outputs, we find an inverse relationship between the scale of the LM and the detectability of its hallucinations.

Understanding Optimal Feature Transfer via a Fine-Grained Bias-Variance Analysis

In the transfer learning paradigm models learn useful representations (or features) during a data-rich pretraining stage, and then use the pretrained representation to improve model performance on data-scarce downstream tasks. In this work, we explore transfer learning with the goal of optimizing downstream performance. We introduce a simple linear model that takes as input an arbitrary pretrained feature transform. We derive exact asymptotics of the downstream risk and its fine-grained bias-variance decomposition. Our finding suggests that using the ground-truth featurization can result in "double-divergence" of the asymptotic risk, indicating that it is not necessarily optimal for downstream performance. We then identify the optimal pretrained representation by minimizing the asymptotic downstream risk averaged over an ensemble of downstream tasks. Our analysis reveals the relative importance of learning the task-relevant features and structures in the data covariates and characterizes how each contributes to controlling the downstream risk from a bias-variance perspective. Moreover, we uncover a phase transition phenomenon where the optimal pretrained representation transitions from hard to soft selection of relevant features and discuss its connection to principal component regression.

Beyond Human Data: Scaling Self-Training for Problem-Solving with Language Models

Fine-tuning language models~(LMs) on human-generated data remains a prevalent practice. However, the performance of such models is often limited by the quantity and diversity of high-quality human data. In this paper, we explore whether we can go beyond human data on tasks where we have access to scalar feedback, for example, on math problems where one can verify correctness. To do so, we investigate a simple self-training method based on expectation-maximization, which we call ReST$^{EM}$, where we (1) generate samples from the model and filter them using binary feedback, (2) fine-tune the model on these samples, and (3) repeat this process a few times. Testing on advanced MATH reasoning and APPS coding benchmarks using PaLM-2 models, we find that ReST$^{EM}$ scales favorably with model size and significantly surpasses fine-tuning only on human data. Overall, our findings suggest self-training with feedback can substantially reduce dependence on human-generated data.

Frontier Language Models are not Robust to Adversarial Arithmetic, or "What do I need to say so you agree 2+2=5?

We introduce and study the problem of adversarial arithmetic, which provides a simple yet challenging testbed for language model alignment. This problem is comprised of arithmetic questions posed in natural language, with an arbitrary adversarial string inserted before the question is complete. Even in the simple setting of 1-digit addition problems, it is easy to find adversarial prompts that make all tested models (including PaLM2, GPT4, Claude2) misbehave, and even to steer models to a particular wrong answer. We additionally provide a simple algorithm for finding successful attacks by querying those same models, which we name "prompt inversion rejection sampling" (PIRS). We finally show that models can be partially hardened against these attacks via reinforcement learning and via agentic constitutional loops. However, we were not able to make a language model fully robust against adversarial arithmetic attacks.

Small-scale proxies for large-scale Transformer training instabilities

Teams that have trained large Transformer-based models have reported training instabilities at large scale that did not appear when training with the same hyperparameters at smaller scales. Although the causes of such instabilities are of scientific interest, the amount of resources required to reproduce them has made investigation difficult. In this work, we seek ways to reproduce and study training stability and instability at smaller scales. First, we focus on two sources of training instability described in previous work: the growth of logits in attention layers (Dehghani et al., 2023) and divergence of the output logits from the log probabilities (Chowdhery et al., 2022). By measuring the relationship between learning rate and loss across scales, we show that these instabilities also appear in small models when training at high learning rates, and that mitigations previously employed at large scales are equally effective in this regime. This prompts us to investigate the extent to which other known optimizer and model interventions influence the sensitivity of the final loss to changes in the learning rate. To this end, we study methods such as warm-up, weight decay, and the $\mu$Param (Yang et al., 2022), and combine techniques to train small models that achieve similar losses across orders of magnitude of learning rate variation. Finally, to conclude our exploration we study two cases where instabilities can be predicted before they emerge by examining the scaling behavior of model activation and gradient norms.

Kernel Regression with Infinite-Width Neural Networks on Millions of Examples

Neural kernels have drastically increased performance on diverse and nonstandard data modalities but require significantly more compute, which previously limited their application to smaller datasets. In this work, we address this by massively parallelizing their computation across many GPUs. We combine this with a distributed, preconditioned conjugate gradients algorithm to enable kernel regression at a large scale (i.e. up to five million examples). Using this approach, we study scaling laws of several neural kernels across many orders of magnitude for the CIFAR-5m dataset. Using data augmentation to expand the original CIFAR-10 training dataset by a factor of 20, we obtain a test accuracy of 91.2\% (SotA for a pure kernel method). Moreover, we explore neural kernels on other data modalities, obtaining results on protein and small molecule prediction tasks that are competitive with SotA methods.

Ensembling over Classifiers: a Bias-Variance Perspective

Ensembles are a straightforward, remarkably effective method for improving the accuracy,calibration, and robustness of models on classification tasks; yet, the reasons that underlie their success remain an active area of research. We build upon the extension to the bias-variance decomposition by Pfau (2013) in order to gain crucial insights into the behavior of ensembles of classifiers. Introducing a dual reparameterization of the bias-variance tradeoff, we first derive generalized laws of total expectation and variance for nonsymmetric losses typical of classification tasks. Comparing conditional and bootstrap bias/variance estimates, we then show that conditional estimates necessarily incur an irreducible error. Next, we show that ensembling in dual space reduces the variance and leaves the bias unchanged, whereas standard ensembling can arbitrarily affect the bias. Empirically, standard ensembling reducesthe bias, leading us to hypothesize that ensembles of classifiers may perform well in part because of this unexpected reduction.We conclude by an empirical analysis of recent deep learning methods that ensemble over hyperparameters, revealing that these techniques indeed favor bias reduction. This suggests that, contrary to classical wisdom, targeting bias reduction may be a promising direction for classifier ensembles.

Implicit Regularization or Implicit Conditioning? Exact Risk Trajectories of SGD in High Dimensions

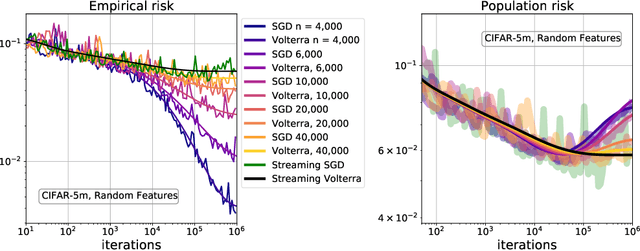
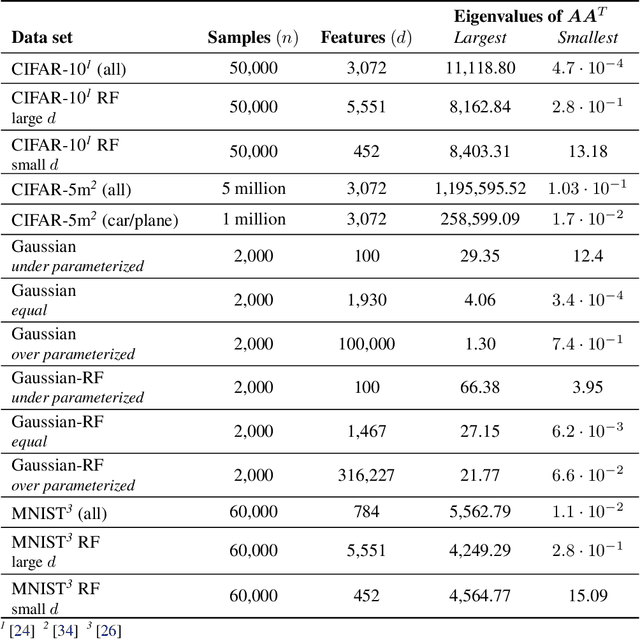
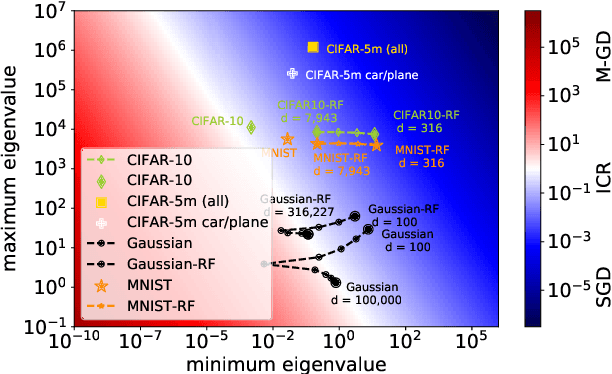
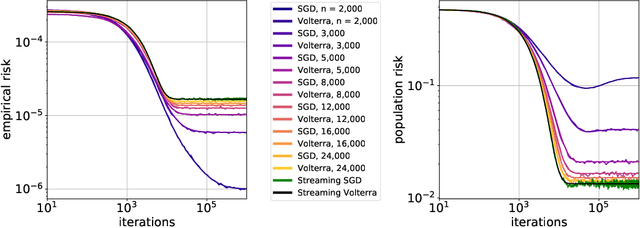
Stochastic gradient descent (SGD) is a pillar of modern machine learning, serving as the go-to optimization algorithm for a diverse array of problems. While the empirical success of SGD is often attributed to its computational efficiency and favorable generalization behavior, neither effect is well understood and disentangling them remains an open problem. Even in the simple setting of convex quadratic problems, worst-case analyses give an asymptotic convergence rate for SGD that is no better than full-batch gradient descent (GD), and the purported implicit regularization effects of SGD lack a precise explanation. In this work, we study the dynamics of multi-pass SGD on high-dimensional convex quadratics and establish an asymptotic equivalence to a stochastic differential equation, which we call homogenized stochastic gradient descent (HSGD), whose solutions we characterize explicitly in terms of a Volterra integral equation. These results yield precise formulas for the learning and risk trajectories, which reveal a mechanism of implicit conditioning that explains the efficiency of SGD relative to GD. We also prove that the noise from SGD negatively impacts generalization performance, ruling out the possibility of any type of implicit regularization in this context. Finally, we show how to adapt the HSGD formalism to include streaming SGD, which allows us to produce an exact prediction for the excess risk of multi-pass SGD relative to that of streaming SGD (bootstrap risk).

Homogenization of SGD in high-dimensions: Exact dynamics and generalization properties

We develop a stochastic differential equation, called homogenized SGD, for analyzing the dynamics of stochastic gradient descent (SGD) on a high-dimensional random least squares problem with $\ell^2$-regularization. We show that homogenized SGD is the high-dimensional equivalence of SGD -- for any quadratic statistic (e.g., population risk with quadratic loss), the statistic under the iterates of SGD converges to the statistic under homogenized SGD when the number of samples $n$ and number of features $d$ are polynomially related ($d^c < n < d^{1/c}$ for some $c > 0$). By analyzing homogenized SGD, we provide exact non-asymptotic high-dimensional expressions for the generalization performance of SGD in terms of a solution of a Volterra integral equation. Further we provide the exact value of the limiting excess risk in the case of quadratic losses when trained by SGD. The analysis is formulated for data matrices and target vectors that satisfy a family of resolvent conditions, which can roughly be viewed as a weak (non-quantitative) form of delocalization of sample-side singular vectors of the data. Several motivating applications are provided including sample covariance matrices with independent samples and random features with non-generative model targets.

Understanding the bias-variance tradeoff of Bregman divergences

This paper builds upon the work of Pfau (2013), which generalized the bias variance tradeoff to any Bregman divergence loss function. Pfau (2013) showed that for Bregman divergences, the bias and variances are defined with respect to a central label, defined as the mean of the label variable, and a central prediction, of a more complex form. We show that, similarly to the label, the central prediction can be interpreted as the mean of a random variable, where the mean operates in a dual space defined by the loss function itself. Viewing the bias-variance tradeoff through operations taken in dual space, we subsequently derive several results of interest. In particular, (a) the variance terms satisfy a generalized law of total variance; (b) if a source of randomness cannot be controlled, its contribution to the bias and variance has a closed form; (c) there exist natural ensembling operations in the label and prediction spaces which reduce the variance and do not affect the bias.