Implicit Regularization or Implicit Conditioning? Exact Risk Trajectories of SGD in High Dimensions
Paper and Code
Jun 15, 2022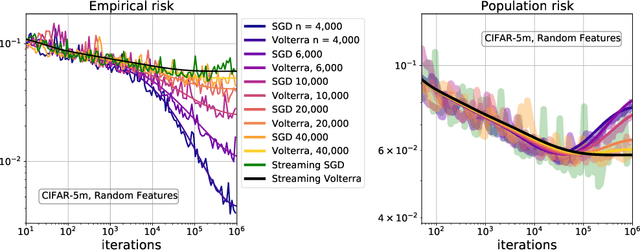
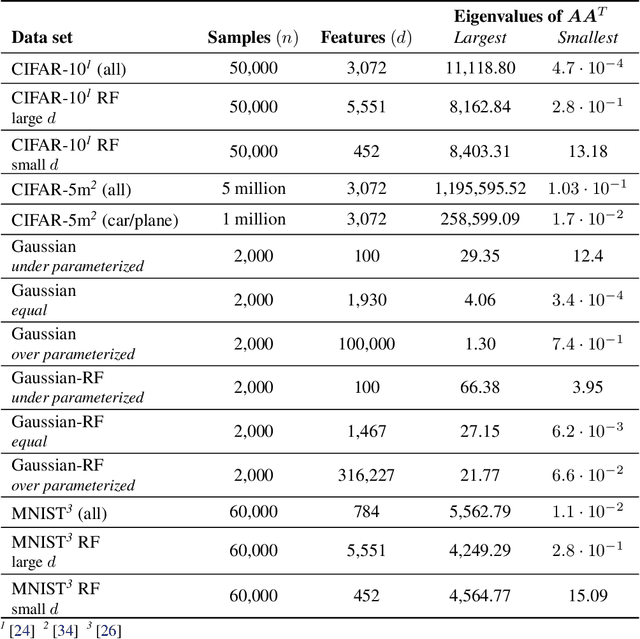
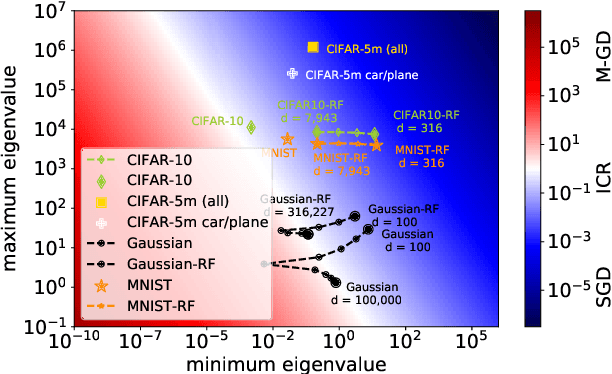
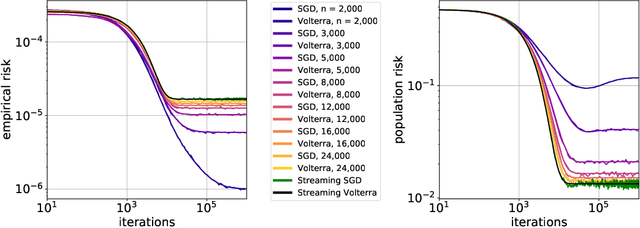
Stochastic gradient descent (SGD) is a pillar of modern machine learning, serving as the go-to optimization algorithm for a diverse array of problems. While the empirical success of SGD is often attributed to its computational efficiency and favorable generalization behavior, neither effect is well understood and disentangling them remains an open problem. Even in the simple setting of convex quadratic problems, worst-case analyses give an asymptotic convergence rate for SGD that is no better than full-batch gradient descent (GD), and the purported implicit regularization effects of SGD lack a precise explanation. In this work, we study the dynamics of multi-pass SGD on high-dimensional convex quadratics and establish an asymptotic equivalence to a stochastic differential equation, which we call homogenized stochastic gradient descent (HSGD), whose solutions we characterize explicitly in terms of a Volterra integral equation. These results yield precise formulas for the learning and risk trajectories, which reveal a mechanism of implicit conditioning that explains the efficiency of SGD relative to GD. We also prove that the noise from SGD negatively impacts generalization performance, ruling out the possibility of any type of implicit regularization in this context. Finally, we show how to adapt the HSGD formalism to include streaming SGD, which allows us to produce an exact prediction for the excess risk of multi-pass SGD relative to that of streaming SGD (bootstrap risk).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge