On conditional diffusion models for PDE simulations

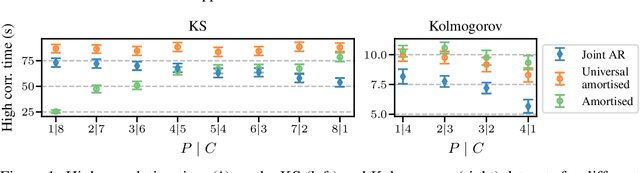
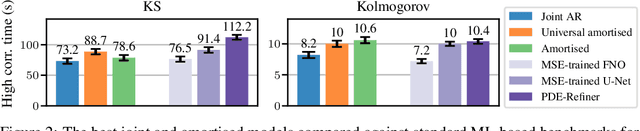
Modelling partial differential equations (PDEs) is of crucial importance in science and engineering, and it includes tasks ranging from forecasting to inverse problems, such as data assimilation. However, most previous numerical and machine learning approaches that target forecasting cannot be applied out-of-the-box for data assimilation. Recently, diffusion models have emerged as a powerful tool for conditional generation, being able to flexibly incorporate observations without retraining. In this work, we perform a comparative study of score-based diffusion models for forecasting and assimilation of sparse observations. In particular, we focus on diffusion models that are either trained in a conditional manner, or conditioned after unconditional training. We address the shortcomings of existing models by proposing 1) an autoregressive sampling approach that significantly improves performance in forecasting, 2) a new training strategy for conditional score-based models that achieves stable performance over a range of history lengths, and 3) a hybrid model which employs flexible pre-training conditioning on initial conditions and flexible post-training conditioning to handle data assimilation. We empirically show that these modifications are crucial for successfully tackling the combination of forecasting and data assimilation, a task commonly encountered in real-world scenarios.

DEFT: Efficient Finetuning of Conditional Diffusion Models by Learning the Generalised $h$-transform

Generative modelling paradigms based on denoising diffusion processes have emerged as a leading candidate for conditional sampling in inverse problems. In many real-world applications, we often have access to large, expensively trained unconditional diffusion models, which we aim to exploit for improving conditional sampling. Most recent approaches are motivated heuristically and lack a unifying framework, obscuring connections between them. Further, they often suffer from issues such as being very sensitive to hyperparameters, being expensive to train or needing access to weights hidden behind a closed API. In this work, we unify conditional training and sampling using the mathematically well-understood Doob's h-transform. This new perspective allows us to unify many existing methods under a common umbrella. Under this framework, we propose DEFT (Doob's h-transform Efficient FineTuning), a new approach for conditional generation that simply fine-tunes a very small network to quickly learn the conditional $h$-transform, while keeping the larger unconditional network unchanged. DEFT is much faster than existing baselines while achieving state-of-the-art performance across a variety of linear and non-linear benchmarks. On image reconstruction tasks, we achieve speedups of up to 1.6$\times$, while having the best perceptual quality on natural images and reconstruction performance on medical images.

Improved motif-scaffolding with SE(3) flow matching

Protein design often begins with knowledge of a desired function from a motif which motif-scaffolding aims to construct a functional protein around. Recently, generative models have achieved breakthrough success in designing scaffolds for a diverse range of motifs. However, the generated scaffolds tend to lack structural diversity, which can hinder success in wet-lab validation. In this work, we extend FrameFlow, an SE(3) flow matching model for protein backbone generation, to perform motif-scaffolding with two complementary approaches. The first is motif amortization, in which FrameFlow is trained with the motif as input using a data augmentation strategy. The second is motif guidance, which performs scaffolding using an estimate of the conditional score from FrameFlow, and requires no additional training. Both approaches achieve an equivalent or higher success rate than previous state-of-the-art methods, with 2.5 times more structurally diverse scaffolds. Code: https://github.com/ microsoft/frame-flow.

A framework for conditional diffusion modelling with applications in motif scaffolding for protein design

Many protein design applications, such as binder or enzyme design, require scaffolding a structural motif with high precision. Generative modelling paradigms based on denoising diffusion processes emerged as a leading candidate to address this motif scaffolding problem and have shown early experimental success in some cases. In the diffusion paradigm, motif scaffolding is treated as a conditional generation task, and several conditional generation protocols were proposed or imported from the Computer Vision literature. However, most of these protocols are motivated heuristically, e.g. via analogies to Langevin dynamics, and lack a unifying framework, obscuring connections between the different approaches. In this work, we unify conditional training and conditional sampling procedures under one common framework based on the mathematically well-understood Doob's h-transform. This new perspective allows us to draw connections between existing methods and propose a new variation on existing conditional training protocols. We illustrate the effectiveness of this new protocol in both, image outpainting and motif scaffolding and find that it outperforms standard methods.

SE(3) Equivariant Augmented Coupling Flows

Coupling normalizing flows allow for fast sampling and density evaluation, making them the tool of choice for probabilistic modeling of physical systems. However, the standard coupling architecture precludes endowing flows that operate on the Cartesian coordinates of atoms with the SE(3) and permutation invariances of physical systems. This work proposes a coupling flow that preserves SE(3) and permutation equivariance by performing coordinate splits along additional augmented dimensions. At each layer, the flow maps atoms' positions into learned SE(3) invariant bases, where we apply standard flow transformations, such as monotonic rational-quadratic splines, before returning to the original basis. Crucially, our flow preserves fast sampling and density evaluation, and may be used to produce unbiased estimates of expectations with respect to the target distribution via importance sampling. When trained on the DW4, LJ13 and QM9-positional datasets, our flow is competitive with equivariant continuous normalizing flows, while allowing sampling two orders of magnitude faster. Moreover, to the best of our knowledge, we are the first to learn the full Boltzmann distribution of alanine dipeptide by only modeling the Cartesian positions of its atoms. Lastly, we demonstrate that our flow can be trained to approximately sample from the Boltzmann distribution of the DW4 and LJ13 particle systems using only their energy functions.

Geometric Neural Diffusion Processes

Denoising diffusion models have proven to be a flexible and effective paradigm for generative modelling. Their recent extension to infinite dimensional Euclidean spaces has allowed for the modelling of stochastic processes. However, many problems in the natural sciences incorporate symmetries and involve data living in non-Euclidean spaces. In this work, we extend the framework of diffusion models to incorporate a series of geometric priors in infinite-dimension modelling. We do so by a) constructing a noising process which admits, as limiting distribution, a geometric Gaussian process that transforms under the symmetry group of interest, and b) approximating the score with a neural network that is equivariant w.r.t. this group. We show that with these conditions, the generative functional model admits the same symmetry. We demonstrate scalability and capacity of the model, using a novel Langevin-based conditional sampler, to fit complex scalar and vector fields, with Euclidean and spherical codomain, on synthetic and real-world weather data.

Metropolis Sampling for Constrained Diffusion Models

Denoising diffusion models have recently emerged as the predominant paradigm for generative modelling. Their extension to Riemannian manifolds has facilitated their application to an array of problems in the natural sciences. Yet, in many practical settings, such manifolds are defined by a set of constraints and are not covered by the existing (Riemannian) diffusion model methodology. Recent work has attempted to address this issue by employing novel noising processes based on logarithmic barrier methods or reflected Brownian motions. However, the associated samplers are computationally burdensome as the complexity of the constraints increases. In this paper, we introduce an alternative simple noising scheme based on Metropolis sampling that affords substantial gains in computational efficiency and empirical performance compared to the earlier samplers. Of independent interest, we prove that this new process corresponds to a valid discretisation of the reflected Brownian motion. We demonstrate the scalability and flexibility of our approach on a range of problem settings with convex and non-convex constraints, including applications from geospatial modelling, robotics and protein design.

Diffusion Models for Constrained Domains

Denoising diffusion models are a recent class of generative models which achieve state-of-the-art results in many domains such as unconditional image generation and text-to-speech tasks. They consist of a noising process destroying the data and a backward stage defined as the time-reversal of the noising diffusion. Building on their success, diffusion models have recently been extended to the Riemannian manifold setting. Yet, these Riemannian diffusion models require geodesics to be defined for all times. While this setting encompasses many important applications, it does not include manifolds defined via a set of inequality constraints, which are ubiquitous in many scientific domains such as robotics and protein design. In this work, we introduce two methods to bridge this gap. First, we design a noising process based on the logarithmic barrier metric induced by the inequality constraints. Second, we introduce a noising process based on the reflected Brownian motion. As existing diffusion model techniques cannot be applied in this setting, we derive new tools to define such models in our framework. We empirically demonstrate the applicability of our methods to a number of synthetic and real-world tasks, including the constrained conformational modelling of protein backbones and robotic arms.

SE(3) diffusion model with application to protein backbone generation

The design of novel protein structures remains a challenge in protein engineering for applications across biomedicine and chemistry. In this line of work, a diffusion model over rigid bodies in 3D (referred to as frames) has shown success in generating novel, functional protein backbones that have not been observed in nature. However, there exists no principled methodological framework for diffusion on SE(3), the space of orientation preserving rigid motions in R3, that operates on frames and confers the group invariance. We address these shortcomings by developing theoretical foundations of SE(3) invariant diffusion models on multiple frames followed by a novel framework, FrameDiff, for learning the SE(3) equivariant score over multiple frames. We apply FrameDiff on monomer backbone generation and find it can generate designable monomers up to 500 amino acids without relying on a pretrained protein structure prediction network that has been integral to previous methods. We find our samples are capable of generalizing beyond any known protein structure.

Spectral Diffusion Processes

Score-based generative modelling (SGM) has proven to be a very effective method for modelling densities on finite-dimensional spaces. In this work we propose to extend this methodology to learn generative models over functional spaces. To do so, we represent functional data in spectral space to dissociate the stochastic part of the processes from their space-time part. Using dimensionality reduction techniques we then sample from their stochastic component using finite dimensional SGM. We demonstrate our method's effectiveness for modelling various multimodal datasets.