Brian L. Trippe
MotifBench: A standardized protein design benchmark for motif-scaffolding problems
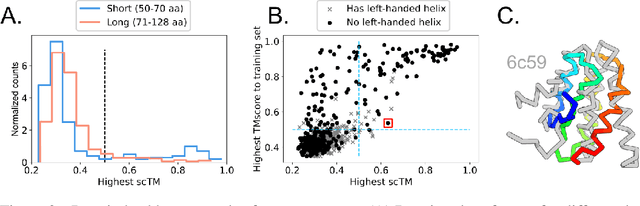
Feb 19, 2025Abstract:The motif-scaffolding problem is a central task in computational protein design: Given the coordinates of atoms in a geometry chosen to confer a desired biochemical function (a motif), the task is to identify diverse protein structures (scaffolds) that include the motif and maintain its geometry. Significant recent progress on motif-scaffolding has been made due to computational evaluation with reliable protein structure prediction and fixed-backbone sequence design methods. However, significant variability in evaluation strategies across publications has hindered comparability of results, challenged reproducibility, and impeded robust progress. In response we introduce MotifBench, comprising (1) a precisely specified pipeline and evaluation metrics, (2) a collection of 30 benchmark problems, and (3) an implementation of this benchmark and leaderboard at github.com/blt2114/MotifBench. The MotifBench test cases are more difficult compared to earlier benchmarks, and include protein design problems for which solutions are known but on which, to the best of our knowledge, state-of-the-art methods fail to identify any solution.
Practical and Asymptotically Exact Conditional Sampling in Diffusion Models
Jun 30, 2023Abstract:Diffusion models have been successful on a range of conditional generation tasks including molecular design and text-to-image generation. However, these achievements have primarily depended on task-specific conditional training or error-prone heuristic approximations. Ideally, a conditional generation method should provide exact samples for a broad range of conditional distributions without requiring task-specific training. To this end, we introduce the Twisted Diffusion Sampler, or TDS. TDS is a sequential Monte Carlo (SMC) algorithm that targets the conditional distributions of diffusion models. The main idea is to use twisting, an SMC technique that enjoys good computational efficiency, to incorporate heuristic approximations without compromising asymptotic exactness. We first find in simulation and on MNIST image inpainting and class-conditional generation tasks that TDS provides a computational statistical trade-off, yielding more accurate approximations with many particles but with empirical improvements over heuristics with as few as two particles. We then turn to motif-scaffolding, a core task in protein design, using a TDS extension to Riemannian diffusion models. On benchmark test cases, TDS allows flexible conditioning criteria and often outperforms the state of the art.
Gaussian processes at the Helm: A more fluid model for ocean currents
Feb 20, 2023



Abstract:Oceanographers are interested in predicting ocean currents and identifying divergences in a current vector field based on sparse observations of buoy velocities. Since we expect current dynamics to be smooth but highly non-linear, Gaussian processes (GPs) offer an attractive model. But we show that applying a GP with a standard stationary kernel directly to buoy data can struggle at both current prediction and divergence identification -- due to some physically unrealistic prior assumptions. To better reflect known physical properties of currents, we propose to instead put a standard stationary kernel on the divergence and curl-free components of a vector field obtained through a Helmholtz decomposition. We show that, because this decomposition relates to the original vector field just via mixed partial derivatives, we can still perform inference given the original data with only a small constant multiple of additional computational expense. We illustrate the benefits of our method on synthetic and real ocean data.
SE(3) diffusion model with application to protein backbone generation
Feb 11, 2023Abstract:The design of novel protein structures remains a challenge in protein engineering for applications across biomedicine and chemistry. In this line of work, a diffusion model over rigid bodies in 3D (referred to as frames) has shown success in generating novel, functional protein backbones that have not been observed in nature. However, there exists no principled methodological framework for diffusion on SE(3), the space of orientation preserving rigid motions in R3, that operates on frames and confers the group invariance. We address these shortcomings by developing theoretical foundations of SE(3) invariant diffusion models on multiple frames followed by a novel framework, FrameDiff, for learning the SE(3) equivariant score over multiple frames. We apply FrameDiff on monomer backbone generation and find it can generate designable monomers up to 500 amino acids without relying on a pretrained protein structure prediction network that has been integral to previous methods. We find our samples are capable of generalizing beyond any known protein structure.
Diffusion probabilistic modeling of protein backbones in 3D for the motif-scaffolding problem
Jun 08, 2022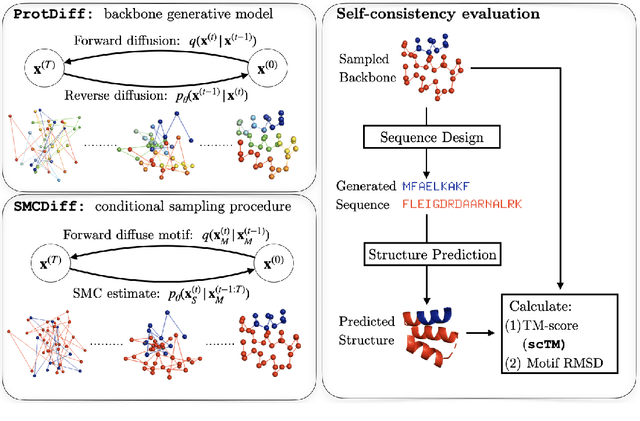
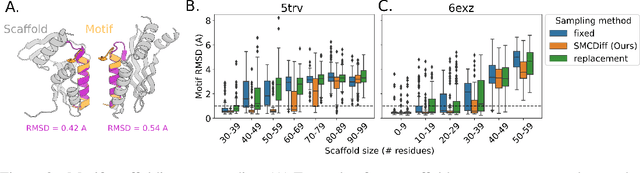
Abstract:Construction of a scaffold structure that supports a desired motif, conferring protein function, shows promise for the design of vaccines and enzymes. But a general solution to this motif-scaffolding problem remains open. Current machine-learning techniques for scaffold design are either limited to unrealistically small scaffolds (up to length 20) or struggle to produce multiple diverse scaffolds. We propose to learn a distribution over diverse and longer protein backbone structures via an E(3)-equivariant graph neural network. We develop SMCDiff to efficiently sample scaffolds from this distribution conditioned on a given motif; our algorithm is the first to theoretically guarantee conditional samples from a diffusion model in the large-compute limit. We evaluate our designed backbones by how well they align with AlphaFold2-predicted structures. We show that our method can (1) sample scaffolds up to 80 residues and (2) achieve structurally diverse scaffolds for a fixed motif.
Many processors, little time: MCMC for partitions via optimal transport couplings
Feb 23, 2022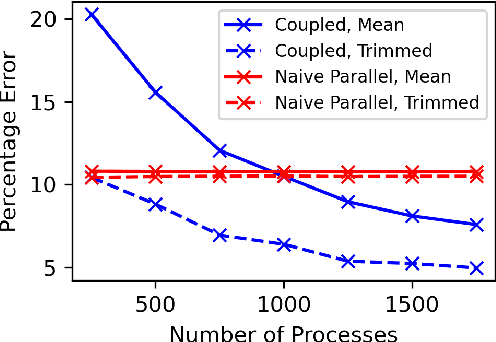
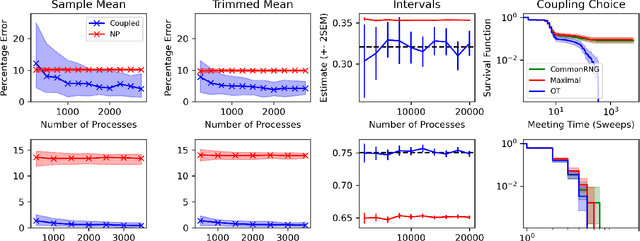
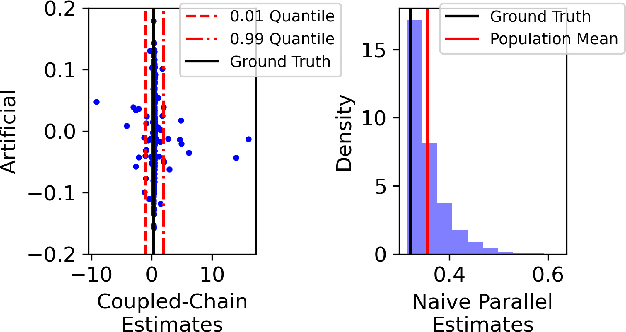
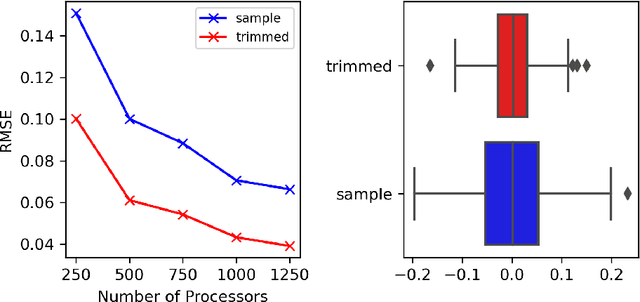
Abstract:Markov chain Monte Carlo (MCMC) methods are often used in clustering since they guarantee asymptotically exact expectations in the infinite-time limit. In finite time, though, slow mixing often leads to poor performance. Modern computing environments offer massive parallelism, but naive implementations of parallel MCMC can exhibit substantial bias. In MCMC samplers of continuous random variables, Markov chain couplings can overcome bias. But these approaches depend crucially on paired chains meetings after a small number of transitions. We show that straightforward applications of existing coupling ideas to discrete clustering variables fail to meet quickly. This failure arises from the "label-switching problem": semantically equivalent cluster relabelings impede fast meeting of coupled chains. We instead consider chains as exploring the space of partitions rather than partitions' (arbitrary) labelings. Using a metric on the partition space, we formulate a practical algorithm using optimal transport couplings. Our theory confirms our method is accurate and efficient. In experiments ranging from clustering of genes or seeds to graph colorings, we show the benefits of our coupling in the highly parallel, time-limited regime.
For high-dimensional hierarchical models, consider exchangeability of effects across covariates instead of across datasets
Jul 13, 2021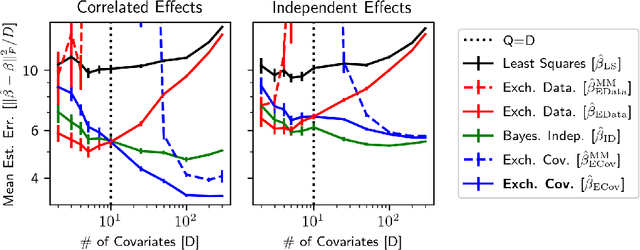
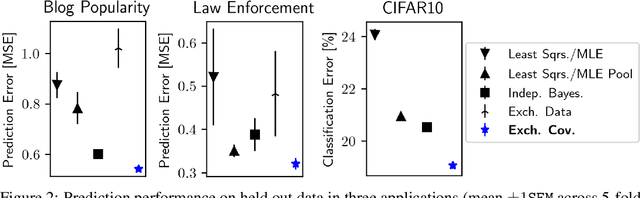
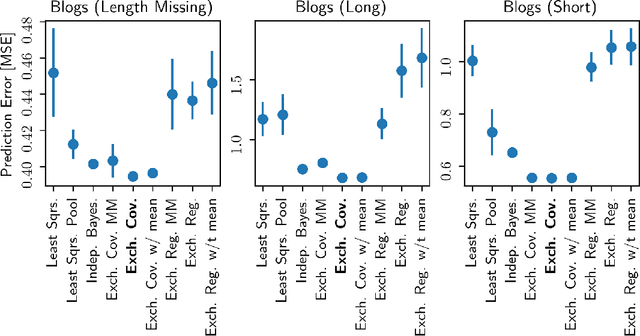
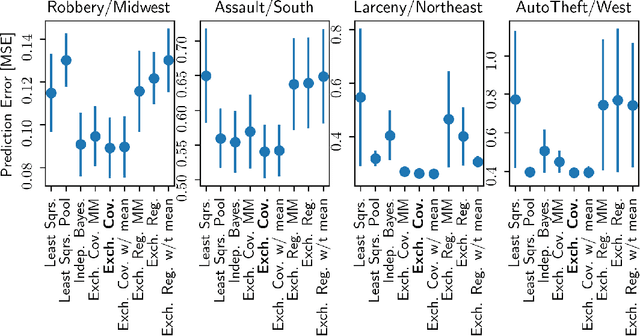
Abstract:Hierarchical Bayesian methods enable information sharing across multiple related regression problems. While standard practice is to model regression parameters (effects) as (1) exchangeable across datasets and (2) correlated to differing degrees across covariates, we show that this approach exhibits poor statistical performance when the number of covariates exceeds the number of datasets. For instance, in statistical genetics, we might regress dozens of traits (defining datasets) for thousands of individuals (responses) on up to millions of genetic variants (covariates). When an analyst has more covariates than datasets, we argue that it is often more natural to instead model effects as (1) exchangeable across covariates and (2) correlated to differing degrees across datasets. To this end, we propose a hierarchical model expressing our alternative perspective. We devise an empirical Bayes estimator for learning the degree of correlation between datasets. We develop theory that demonstrates that our method outperforms the classic approach when the number of covariates dominates the number of datasets, and corroborate this result empirically on several high-dimensional multiple regression and classification problems.
LR-GLM: High-Dimensional Bayesian Inference Using Low-Rank Data Approximations
May 17, 2019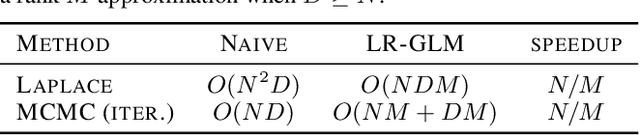
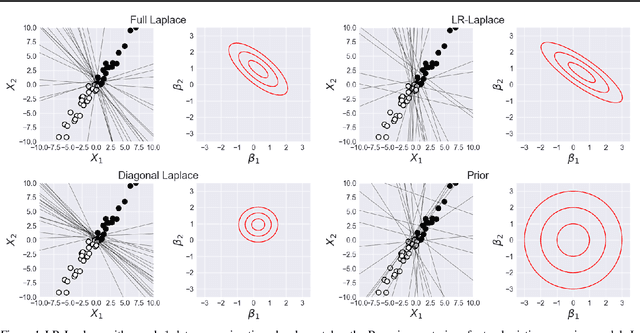
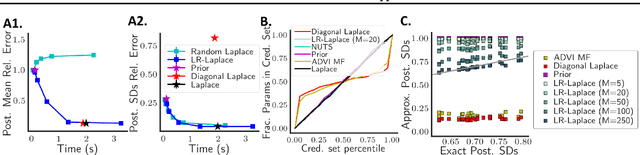
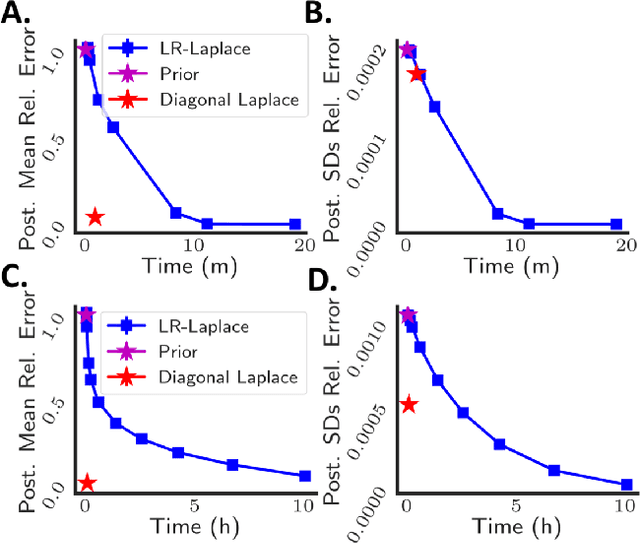
Abstract:Due to the ease of modern data collection, applied statisticians often have access to a large set of covariates that they wish to relate to some observed outcome. Generalized linear models (GLMs) offer a particularly interpretable framework for such an analysis. In these high-dimensional problems, the number of covariates is often large relative to the number of observations, so we face non-trivial inferential uncertainty; a Bayesian approach allows coherent quantification of this uncertainty. Unfortunately, existing methods for Bayesian inference in GLMs require running times roughly cubic in parameter dimension, and so are limited to settings with at most tens of thousand parameters. We propose to reduce time and memory costs with a low-rank approximation of the data in an approach we call LR-GLM. When used with the Laplace approximation or Markov chain Monte Carlo, LR-GLM provides a full Bayesian posterior approximation and admits running times reduced by a full factor of the parameter dimension. We rigorously establish the quality of our approximation and show how the choice of rank allows a tunable computational-statistical trade-off. Experiments support our theory and demonstrate the efficacy of LR-GLM on real large-scale datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge