For high-dimensional hierarchical models, consider exchangeability of effects across covariates instead of across datasets

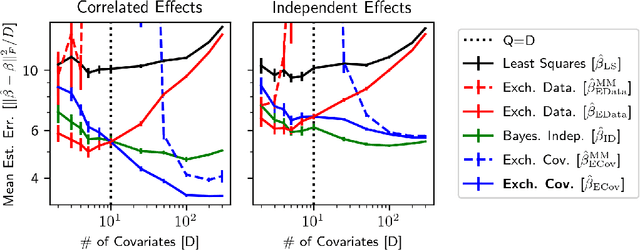
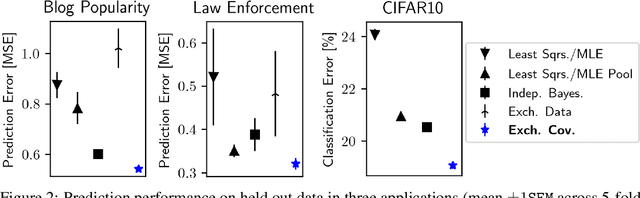
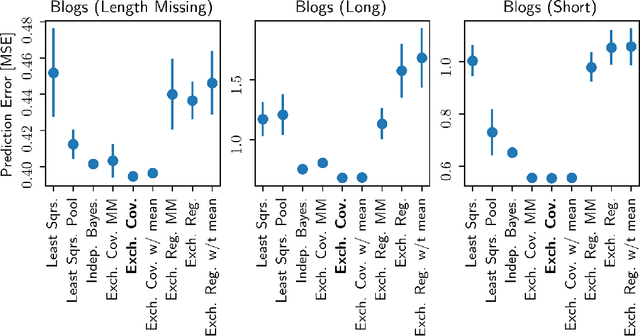
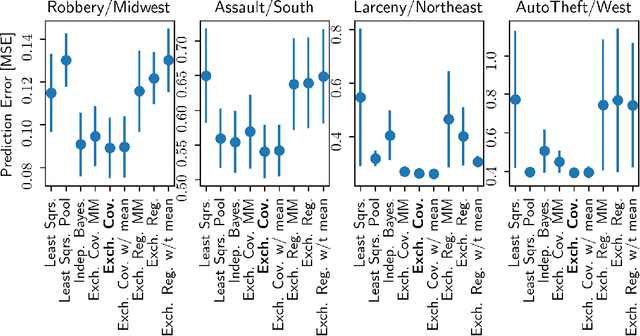
Hierarchical Bayesian methods enable information sharing across multiple related regression problems. While standard practice is to model regression parameters (effects) as (1) exchangeable across datasets and (2) correlated to differing degrees across covariates, we show that this approach exhibits poor statistical performance when the number of covariates exceeds the number of datasets. For instance, in statistical genetics, we might regress dozens of traits (defining datasets) for thousands of individuals (responses) on up to millions of genetic variants (covariates). When an analyst has more covariates than datasets, we argue that it is often more natural to instead model effects as (1) exchangeable across covariates and (2) correlated to differing degrees across datasets. To this end, we propose a hierarchical model expressing our alternative perspective. We devise an empirical Bayes estimator for learning the degree of correlation between datasets. We develop theory that demonstrates that our method outperforms the classic approach when the number of covariates dominates the number of datasets, and corroborate this result empirically on several high-dimensional multiple regression and classification problems.

Measuring dependence powerfully and equitably

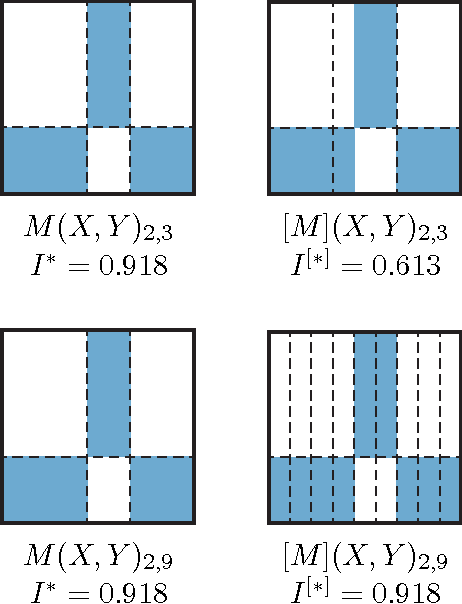
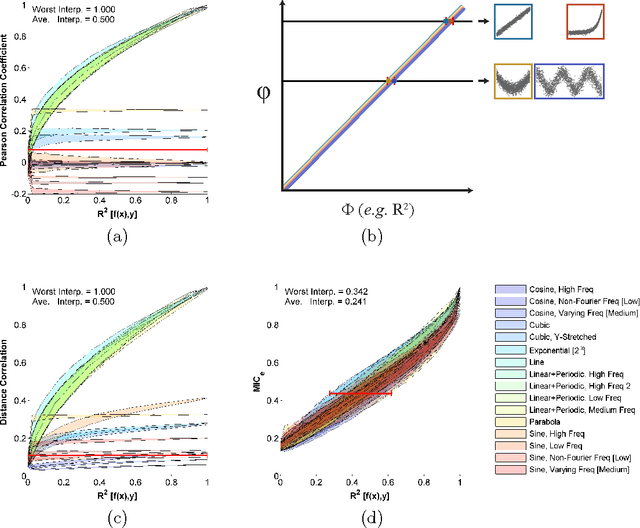
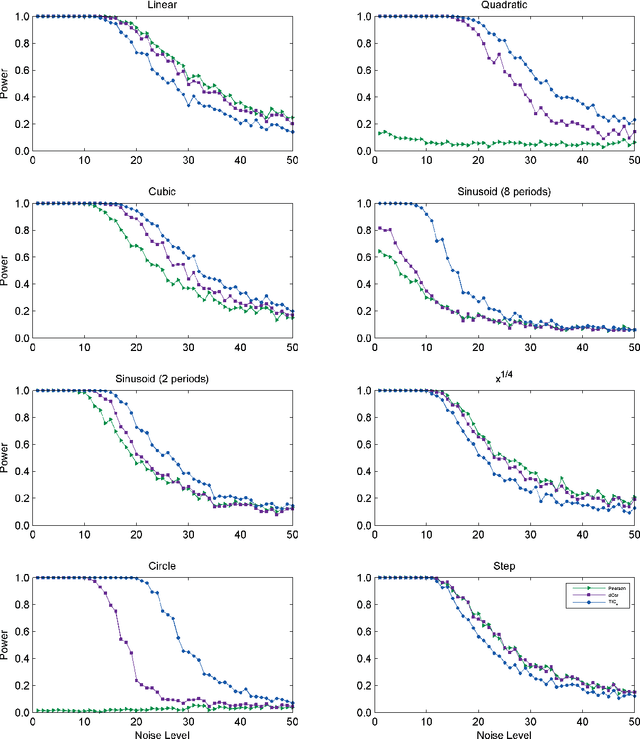
Given a high-dimensional data set we often wish to find the strongest relationships within it. A common strategy is to evaluate a measure of dependence on every variable pair and retain the highest-scoring pairs for follow-up. This strategy works well if the statistic used is equitable [Reshef et al. 2015a], i.e., if, for some measure of noise, it assigns similar scores to equally noisy relationships regardless of relationship type (e.g., linear, exponential, periodic). In this paper, we introduce and characterize a population measure of dependence called MIC*. We show three ways that MIC* can be viewed: as the population value of MIC, a highly equitable statistic from [Reshef et al. 2011], as a canonical "smoothing" of mutual information, and as the supremum of an infinite sequence defined in terms of optimal one-dimensional partitions of the marginals of the joint distribution. Based on this theory, we introduce an efficient approach for computing MIC* from the density of a pair of random variables, and we define a new consistent estimator MICe for MIC* that is efficiently computable. In contrast, there is no known polynomial-time algorithm for computing the original equitable statistic MIC. We show through simulations that MICe has better bias-variance properties than MIC. We then introduce and prove the consistency of a second statistic, TICe, that is a trivial side-product of the computation of MICe and whose goal is powerful independence testing rather than equitability. We show in simulations that MICe and TICe have good equitability and power against independence respectively. The analyses here complement a more in-depth empirical evaluation of several leading measures of dependence [Reshef et al. 2015b] that shows state-of-the-art performance for MICe and TICe.