Michael M. Mitzenmacher
Weightless: Lossy Weight Encoding For Deep Neural Network Compression
Nov 13, 2017
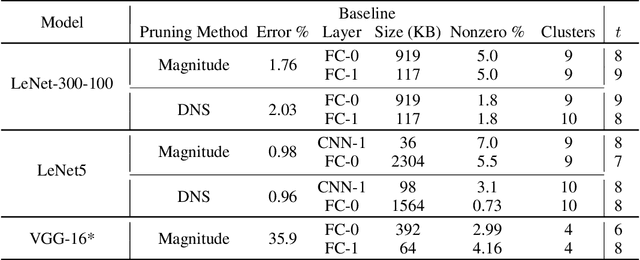

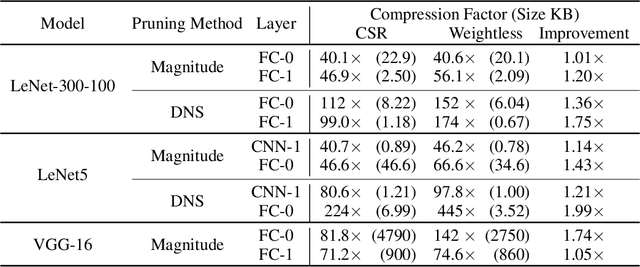
Abstract:The large memory requirements of deep neural networks limit their deployment and adoption on many devices. Model compression methods effectively reduce the memory requirements of these models, usually through applying transformations such as weight pruning or quantization. In this paper, we present a novel scheme for lossy weight encoding which complements conventional compression techniques. The encoding is based on the Bloomier filter, a probabilistic data structure that can save space at the cost of introducing random errors. Leveraging the ability of neural networks to tolerate these imperfections and by re-training around the errors, the proposed technique, Weightless, can compress DNN weights by up to 496x with the same model accuracy. This results in up to a 1.51x improvement over the state-of-the-art.
Measuring dependence powerfully and equitably
Jul 06, 2016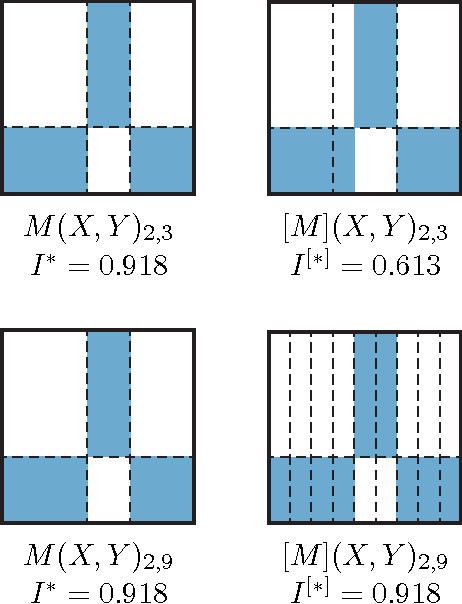

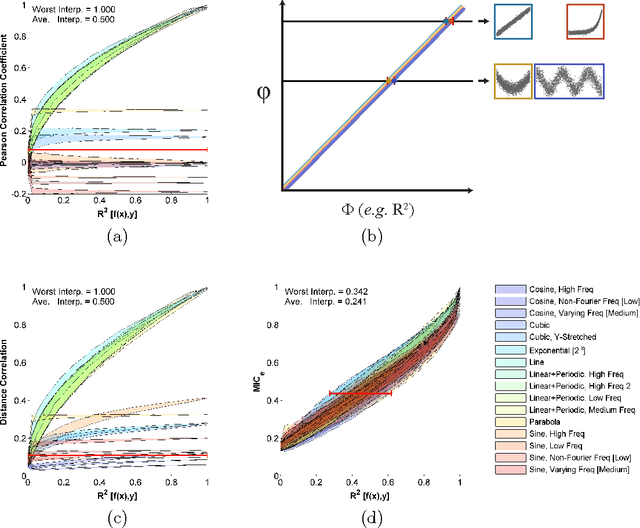
Abstract:Given a high-dimensional data set we often wish to find the strongest relationships within it. A common strategy is to evaluate a measure of dependence on every variable pair and retain the highest-scoring pairs for follow-up. This strategy works well if the statistic used is equitable [Reshef et al. 2015a], i.e., if, for some measure of noise, it assigns similar scores to equally noisy relationships regardless of relationship type (e.g., linear, exponential, periodic). In this paper, we introduce and characterize a population measure of dependence called MIC*. We show three ways that MIC* can be viewed: as the population value of MIC, a highly equitable statistic from [Reshef et al. 2011], as a canonical "smoothing" of mutual information, and as the supremum of an infinite sequence defined in terms of optimal one-dimensional partitions of the marginals of the joint distribution. Based on this theory, we introduce an efficient approach for computing MIC* from the density of a pair of random variables, and we define a new consistent estimator MICe for MIC* that is efficiently computable. In contrast, there is no known polynomial-time algorithm for computing the original equitable statistic MIC. We show through simulations that MICe has better bias-variance properties than MIC. We then introduce and prove the consistency of a second statistic, TICe, that is a trivial side-product of the computation of MICe and whose goal is powerful independence testing rather than equitability. We show in simulations that MICe and TICe have good equitability and power against independence respectively. The analyses here complement a more in-depth empirical evaluation of several leading measures of dependence [Reshef et al. 2015b] that shows state-of-the-art performance for MICe and TICe.
* Yakir A. Reshef and David N. Reshef are co-first authors, Pardis C. Sabeti and Michael M. Mitzenmacher are co-last authors. This paper, together with arXiv:1505.02212, subsumes arXiv:1408.4908. v3 includes new analyses and exposition
Equitability, interval estimation, and statistical power
May 12, 2015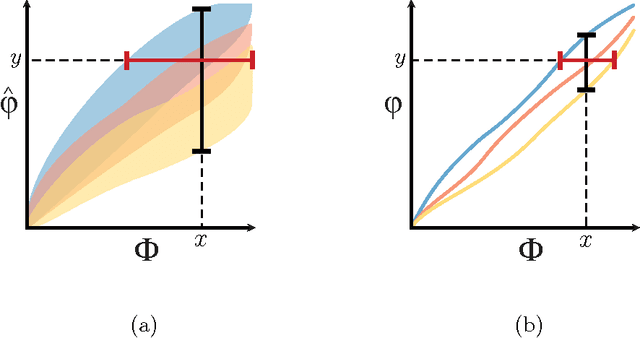
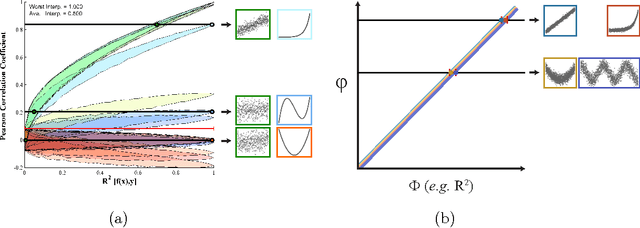
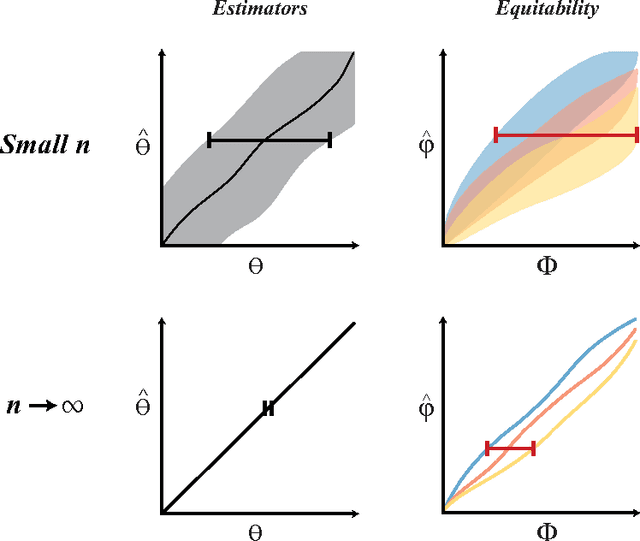
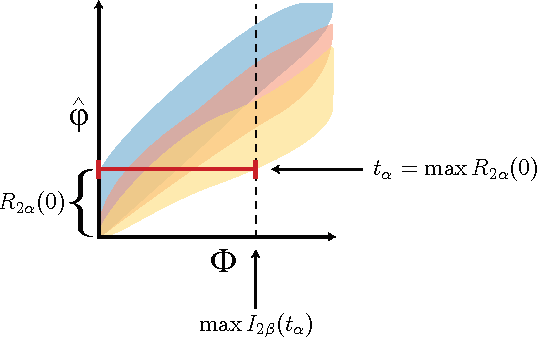
Abstract:For analysis of a high-dimensional dataset, a common approach is to test a null hypothesis of statistical independence on all variable pairs using a non-parametric measure of dependence. However, because this approach attempts to identify any non-trivial relationship no matter how weak, it often identifies too many relationships to be useful. What is needed is a way of identifying a smaller set of relationships that merit detailed further analysis. Here we formally present and characterize equitability, a property of measures of dependence that aims to overcome this challenge. Notionally, an equitable statistic is a statistic that, given some measure of noise, assigns similar scores to equally noisy relationships of different types [Reshef et al. 2011]. We begin by formalizing this idea via a new object called the interpretable interval, which functions as an interval estimate of the amount of noise in a relationship of unknown type. We define an equitable statistic as one with small interpretable intervals. We then draw on the equivalence of interval estimation and hypothesis testing to show that under moderate assumptions an equitable statistic is one that yields well powered tests for distinguishing not only between trivial and non-trivial relationships of all kinds but also between non-trivial relationships of different strengths. This means that equitability allows us to specify a threshold relationship strength $x_0$ and to search for relationships of all kinds with strength greater than $x_0$. Thus, equitability can be thought of as a strengthening of power against independence that enables fruitful analysis of data sets with a small number of strong, interesting relationships and a large number of weaker ones. We conclude with a demonstration of how our two equivalent characterizations of equitability can be used to evaluate the equitability of a statistic in practice.
An Empirical Study of Leading Measures of Dependence
May 12, 2015
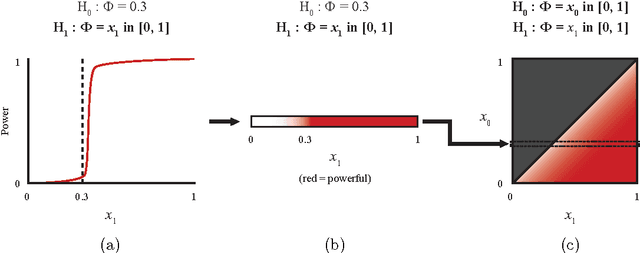

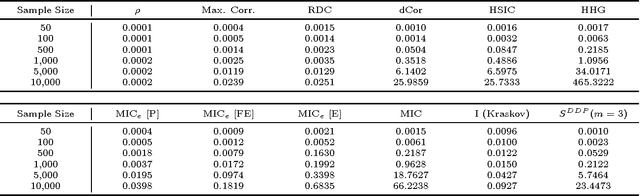
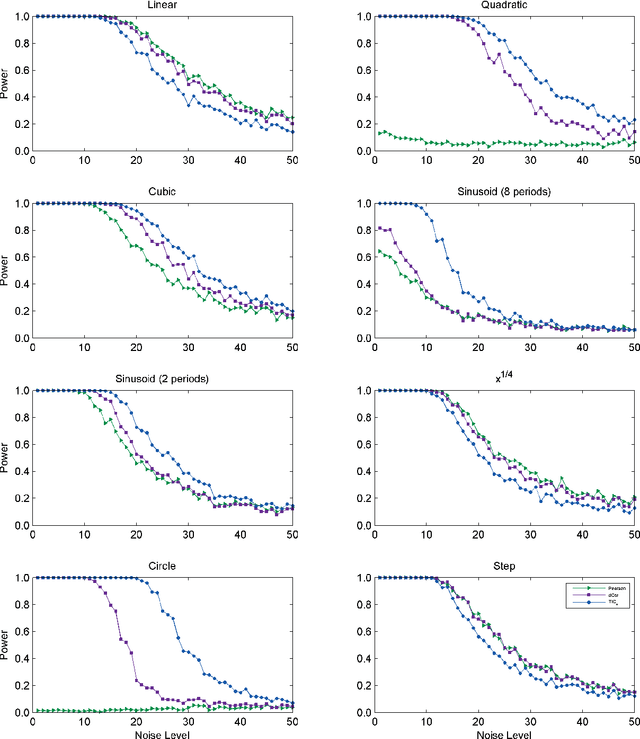
Abstract:In exploratory data analysis, we are often interested in identifying promising pairwise associations for further analysis while filtering out weaker, less interesting ones. This can be accomplished by computing a measure of dependence on all variable pairs and examining the highest-scoring pairs, provided the measure of dependence used assigns similar scores to equally noisy relationships of different types. This property, called equitability, is formalized in Reshef et al. [2015b]. In addition to equitability, measures of dependence can also be assessed by the power of their corresponding independence tests as well as their runtime. Here we present extensive empirical evaluation of the equitability, power against independence, and runtime of several leading measures of dependence. These include two statistics introduced in Reshef et al. [2015a]: MICe, which has equitability as its primary goal, and TICe, which has power against independence as its goal. Regarding equitability, our analysis finds that MICe is the most equitable method on functional relationships in most of the settings we considered, although mutual information estimation proves the most equitable at large sample sizes in some specific settings. Regarding power against independence, we find that TICe, along with Heller and Gorfine's S^DDP, is the state of the art on the relationships we tested. Our analyses also show a trade-off between power against independence and equitability consistent with the theory in Reshef et al. [2015b]. In terms of runtime, MICe and TICe are significantly faster than many other measures of dependence tested, and computing either one makes computing the other trivial. This suggests that a fast and useful strategy for achieving a combination of power against independence and equitability may be to filter relationships by TICe and then to examine the MICe of only the significant ones.
* David N. Reshef and Yakir A. Reshef are co-first authors, Pardis C. Sabeti and Michael M. Mitzenmacher are co-last authors
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge