Equitability, interval estimation, and statistical power
Paper and Code
May 12, 2015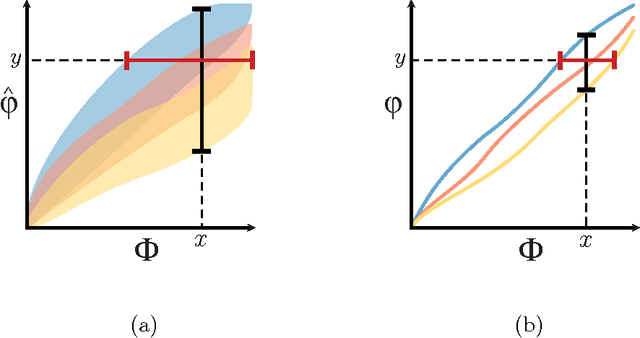
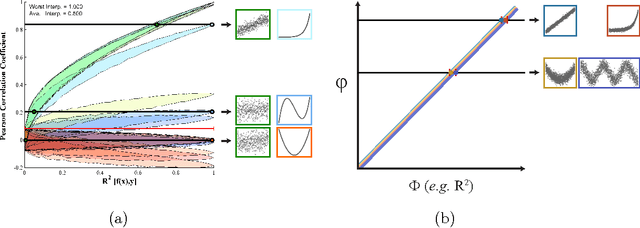
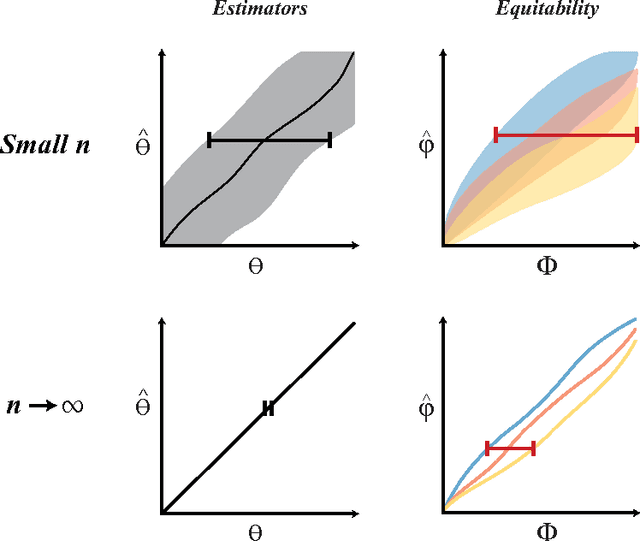
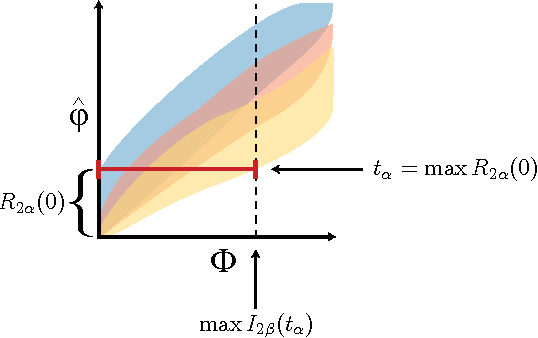
For analysis of a high-dimensional dataset, a common approach is to test a null hypothesis of statistical independence on all variable pairs using a non-parametric measure of dependence. However, because this approach attempts to identify any non-trivial relationship no matter how weak, it often identifies too many relationships to be useful. What is needed is a way of identifying a smaller set of relationships that merit detailed further analysis. Here we formally present and characterize equitability, a property of measures of dependence that aims to overcome this challenge. Notionally, an equitable statistic is a statistic that, given some measure of noise, assigns similar scores to equally noisy relationships of different types [Reshef et al. 2011]. We begin by formalizing this idea via a new object called the interpretable interval, which functions as an interval estimate of the amount of noise in a relationship of unknown type. We define an equitable statistic as one with small interpretable intervals. We then draw on the equivalence of interval estimation and hypothesis testing to show that under moderate assumptions an equitable statistic is one that yields well powered tests for distinguishing not only between trivial and non-trivial relationships of all kinds but also between non-trivial relationships of different strengths. This means that equitability allows us to specify a threshold relationship strength $x_0$ and to search for relationships of all kinds with strength greater than $x_0$. Thus, equitability can be thought of as a strengthening of power against independence that enables fruitful analysis of data sets with a small number of strong, interesting relationships and a large number of weaker ones. We conclude with a demonstration of how our two equivalent characterizations of equitability can be used to evaluate the equitability of a statistic in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge