An Empirical Study of Leading Measures of Dependence

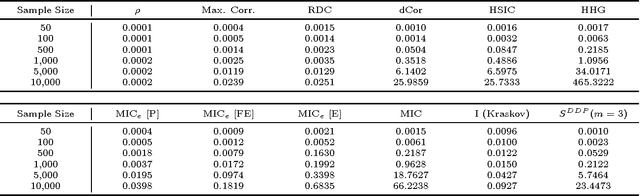
In exploratory data analysis, we are often interested in identifying promising pairwise associations for further analysis while filtering out weaker, less interesting ones. This can be accomplished by computing a measure of dependence on all variable pairs and examining the highest-scoring pairs, provided the measure of dependence used assigns similar scores to equally noisy relationships of different types. This property, called equitability, is formalized in Reshef et al. [2015b]. In addition to equitability, measures of dependence can also be assessed by the power of their corresponding independence tests as well as their runtime. Here we present extensive empirical evaluation of the equitability, power against independence, and runtime of several leading measures of dependence. These include two statistics introduced in Reshef et al. [2015a]: MICe, which has equitability as its primary goal, and TICe, which has power against independence as its goal. Regarding equitability, our analysis finds that MICe is the most equitable method on functional relationships in most of the settings we considered, although mutual information estimation proves the most equitable at large sample sizes in some specific settings. Regarding power against independence, we find that TICe, along with Heller and Gorfine's S^DDP, is the state of the art on the relationships we tested. Our analyses also show a trade-off between power against independence and equitability consistent with the theory in Reshef et al. [2015b]. In terms of runtime, MICe and TICe are significantly faster than many other measures of dependence tested, and computing either one makes computing the other trivial. This suggests that a fast and useful strategy for achieving a combination of power against independence and equitability may be to filter relationships by TICe and then to examine the MICe of only the significant ones.