On Regularization and Inference with Label Constraints

Prior knowledge and symbolic rules in machine learning are often expressed in the form of label constraints, especially in structured prediction problems. In this work, we compare two common strategies for encoding label constraints in a machine learning pipeline, regularization with constraints and constrained inference, by quantifying their impact on model performance. For regularization, we show that it narrows the generalization gap by precluding models that are inconsistent with the constraints. However, its preference for small violations introduces a bias toward a suboptimal model. For constrained inference, we show that it reduces the population risk by correcting a model's violation, and hence turns the violation into an advantage. Given these differences, we further explore the use of two approaches together and propose conditions for constrained inference to compensate for the bias introduced by regularization, aiming to improve both the model complexity and optimal risk.

Are you using test log-likelihood correctly?

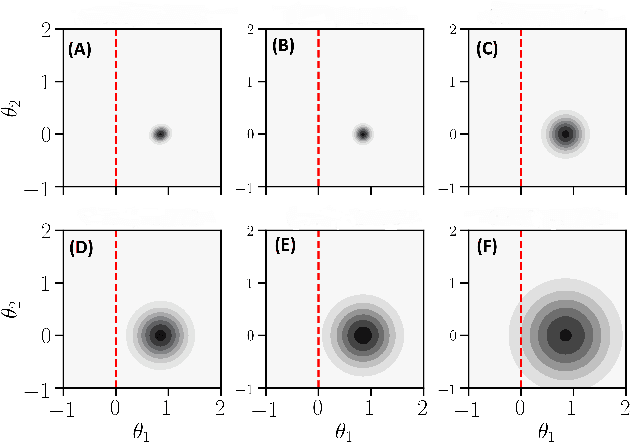
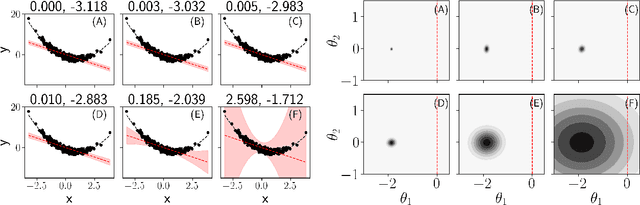
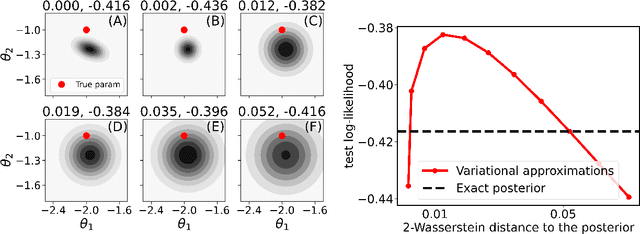
Test log-likelihood is commonly used to compare different models of the same data and different approximate inference algorithms for fitting the same probabilistic model. We present simple examples demonstrating how comparisons based on test log-likelihood can contradict comparisons according to other objectives. Specifically, our examples show that (i) conclusions about forecast accuracy based on test log-likelihood comparisons may not agree with conclusions based on other distributional quantities like means; and (ii) that approximate Bayesian inference algorithms that attain higher test log-likelihoods need not also yield more accurate posterior approximations.

Many processors, little time: MCMC for partitions via optimal transport couplings

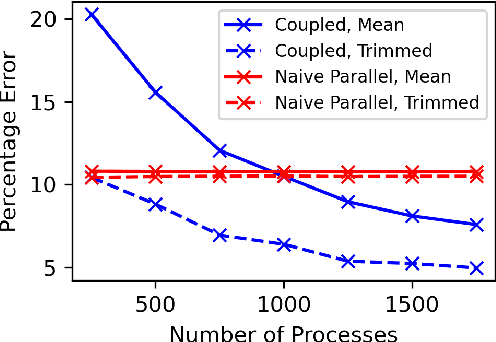
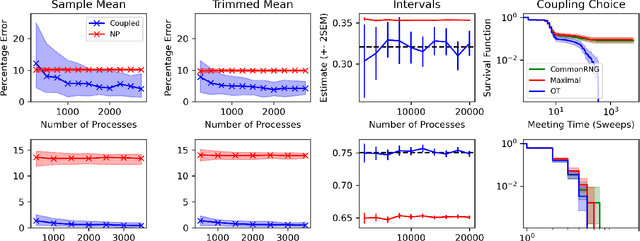
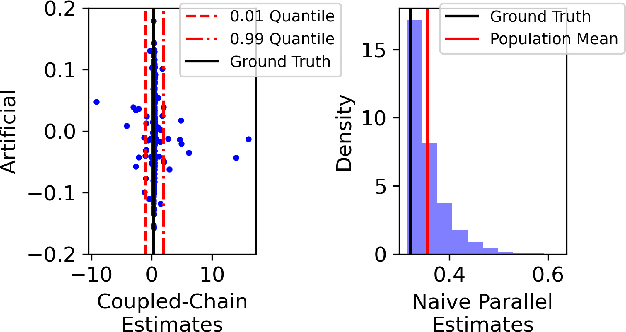
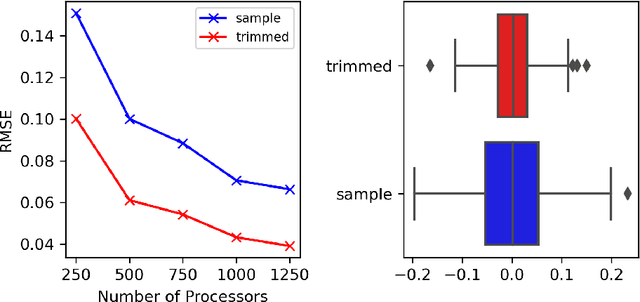
Markov chain Monte Carlo (MCMC) methods are often used in clustering since they guarantee asymptotically exact expectations in the infinite-time limit. In finite time, though, slow mixing often leads to poor performance. Modern computing environments offer massive parallelism, but naive implementations of parallel MCMC can exhibit substantial bias. In MCMC samplers of continuous random variables, Markov chain couplings can overcome bias. But these approaches depend crucially on paired chains meetings after a small number of transitions. We show that straightforward applications of existing coupling ideas to discrete clustering variables fail to meet quickly. This failure arises from the "label-switching problem": semantically equivalent cluster relabelings impede fast meeting of coupled chains. We instead consider chains as exploring the space of partitions rather than partitions' (arbitrary) labelings. Using a metric on the partition space, we formulate a practical algorithm using optimal transport couplings. Our theory confirms our method is accurate and efficient. In experiments ranging from clustering of genes or seeds to graph colorings, we show the benefits of our coupling in the highly parallel, time-limited regime.

Measuring the sensitivity of Gaussian processes to kernel choice

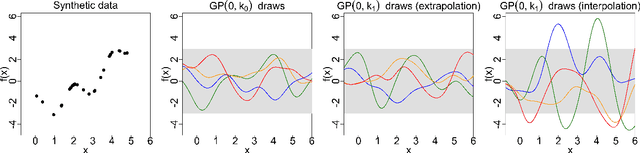
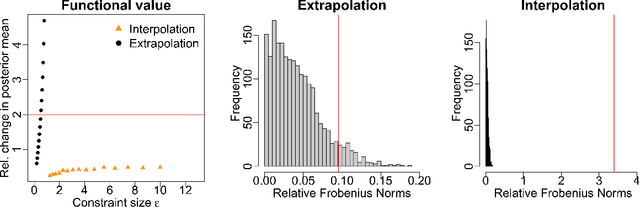
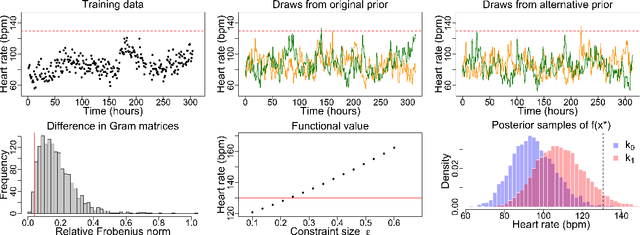
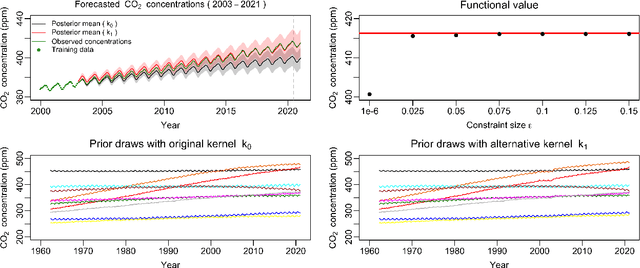
Gaussian processes (GPs) are used to make medical and scientific decisions, including in cardiac care and monitoring of carbon dioxide emissions. But the choice of GP kernel is often somewhat arbitrary. In particular, uncountably many kernels typically align with qualitative prior knowledge (e.g. function smoothness or stationarity). But in practice, data analysts choose among a handful of convenient standard kernels (e.g. squared exponential). In the present work, we ask: Would decisions made with a GP differ under other, qualitatively interchangeable kernels? We show how to formulate this sensitivity analysis as a constrained optimization problem over a finite-dimensional space. We can then use standard optimizers to identify substantive changes in relevant decisions made with a GP. We demonstrate in both synthetic and real-world examples that decisions made with a GP can exhibit substantial sensitivity to kernel choice, even when prior draws are qualitatively interchangeable to a user.

Independent finite approximations for Bayesian nonparametric inference: construction, error bounds, and practical implications

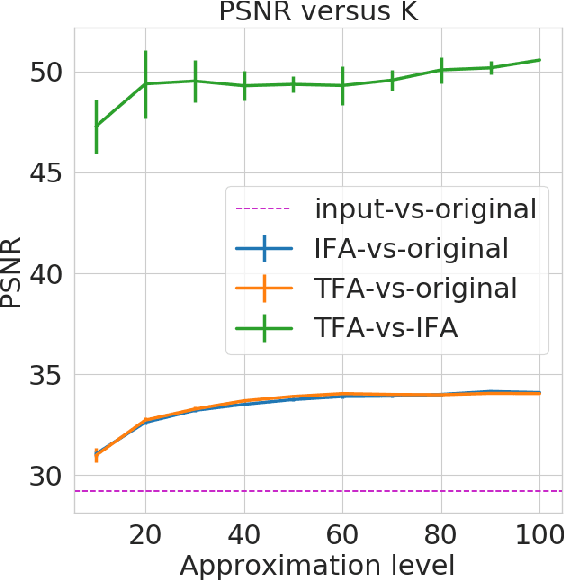
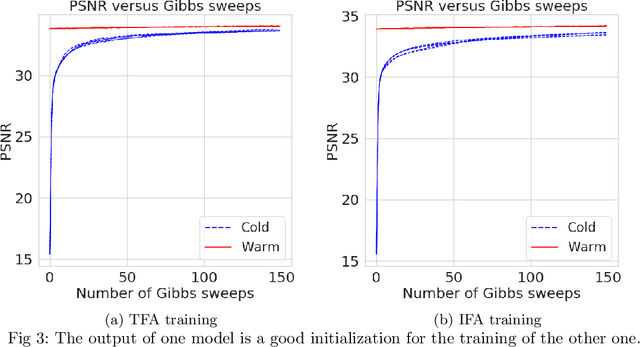
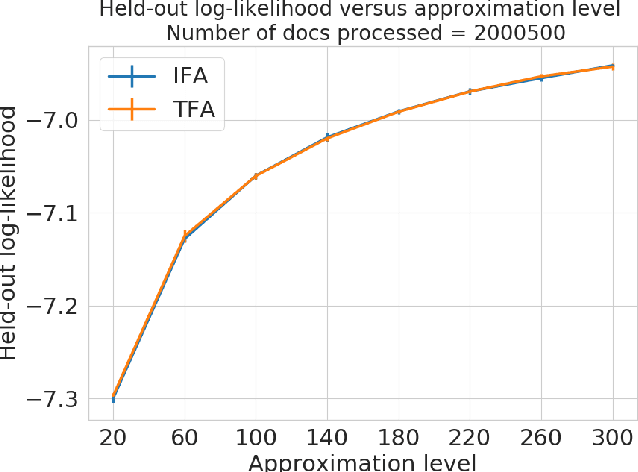
Bayesian nonparametrics based on completely random measures (CRMs) offers a flexible modeling approach when the number of clusters or latent components in a dataset is unknown. However, managing the infinite dimensionality of CRMs often leads to slow computation. Practical inference typically relies on either integrating out the infinite-dimensional parameter or using a finite approximation: a truncated finite approximation (TFA) or an independent finite approximation (IFA). The atom weights of TFAs are constructed sequentially, while the atoms of IFAs are independent, which (1) make them well-suited for parallel and distributed computation and (2) facilitates more convenient inference schemes. While IFAs have been developed in certain special cases in the past, there has not yet been a general template for construction or a systematic comparison to TFAs. We show how to construct IFAs for approximating distributions in a large family of CRMs, encompassing all those typically used in practice. We quantify the approximation error between IFAs and the target nonparametric prior, and prove that, in the worst-case, TFAs provide more component-efficient approximations than IFAs. However, in experiments on image denoising and topic modeling tasks with real data, we find that the error of Bayesian approximation methods overwhelms any finite approximation error, and IFAs perform very similarly to TFAs.

Approximate Cross-Validation for Structured Models

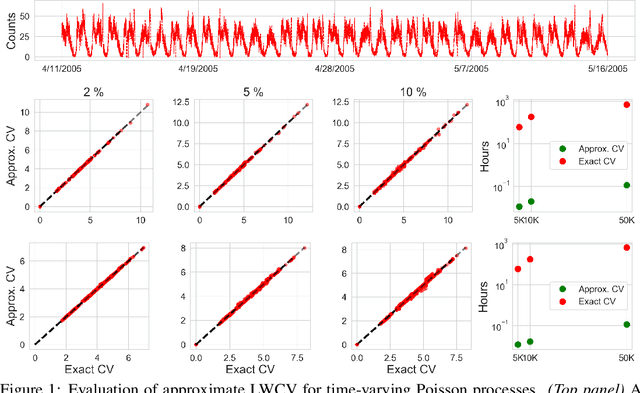
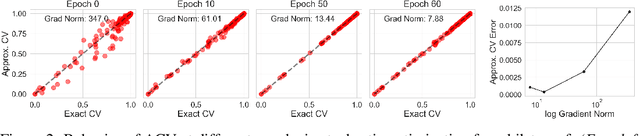
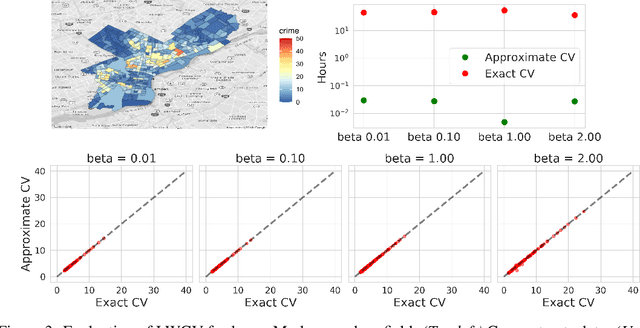
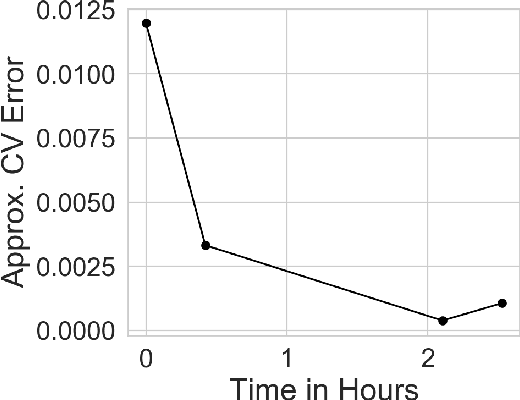
Many modern data analyses benefit from explicitly modeling dependence structure in data -- such as measurements across time or space, ordered words in a sentence, or genes in a genome. Cross-validation is the gold standard to evaluate these analyses but can be prohibitively slow due to the need to re-run already-expensive learning algorithms many times. Previous work has shown approximate cross-validation (ACV) methods provide a fast and provably accurate alternative in the setting of empirical risk minimization. But this existing ACV work is restricted to simpler models by the assumptions that (i) data are independent and (ii) an exact initial model fit is available. In structured data analyses, (i) is always untrue, and (ii) is often untrue. In the present work, we address (i) by extending ACV to models with dependence structure. To address (ii), we verify -- both theoretically and empirically -- that ACV quality deteriorates smoothly with noise in the initial fit. We demonstrate the accuracy and computational benefits of our proposed methods on a diverse set of real-world applications.