Challenges and Opportunities in High-dimensional Variational Inference

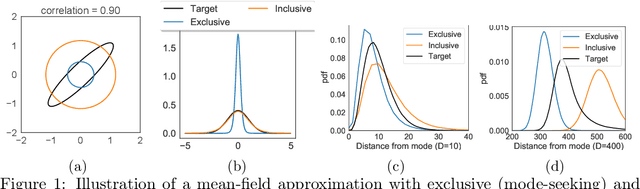
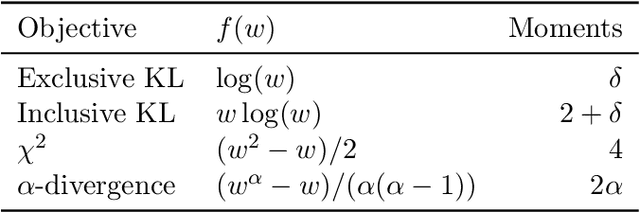
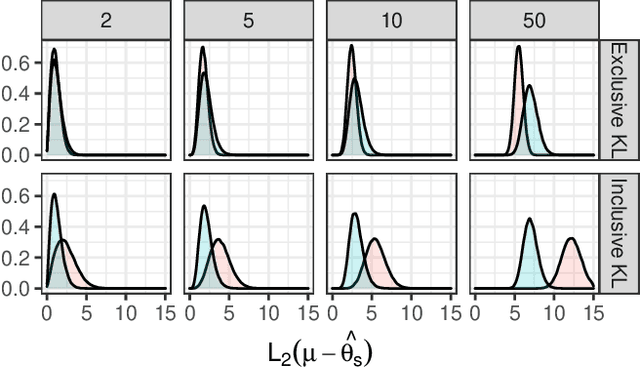
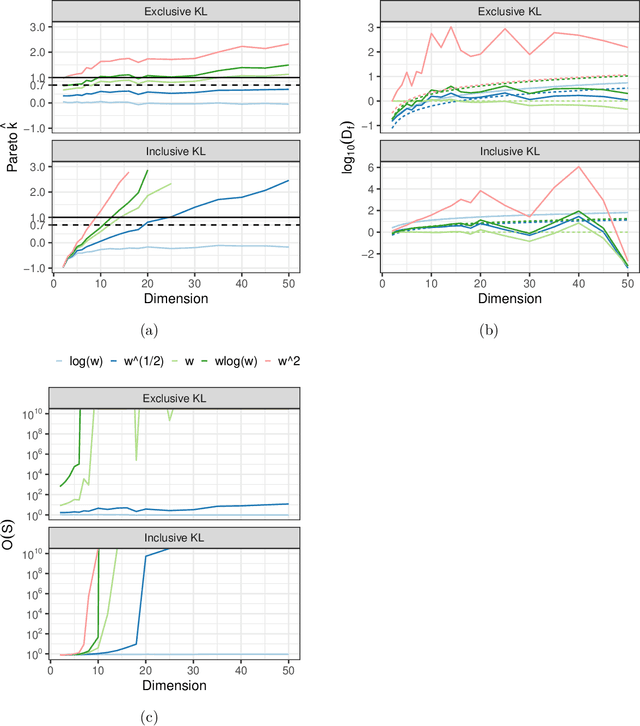
We explore the limitations of and best practices for using black-box variational inference to estimate posterior summaries of the model parameters. By taking an importance sampling perspective, we are able to explain and empirically demonstrate: 1) why the intuitions about the behavior of approximate families and divergences for low-dimensional posteriors fail for higher-dimensional posteriors, 2) how we can diagnose the pre-asymptotic reliability of variational inference in practice by examining the behavior of the density ratios (i.e., importance weights), 3) why the choice of variational objective is not as relevant for higher-dimensional posteriors, and 4) why, although flexible variational families can provide some benefits in higher dimensions, they also introduce additional optimization challenges. Based on these findings, for high-dimensional posteriors we recommend using the exclusive KL divergence that is most stable and easiest to optimize, and then focusing on improving the variational family or using model parameter transformations to make the posterior more similar to the approximating family. Our results also show that in low to moderate dimensions, heavy-tailed variational families and mass-covering divergences can increase the chances that the approximation can be improved by importance sampling.

Independent finite approximations for Bayesian nonparametric inference: construction, error bounds, and practical implications

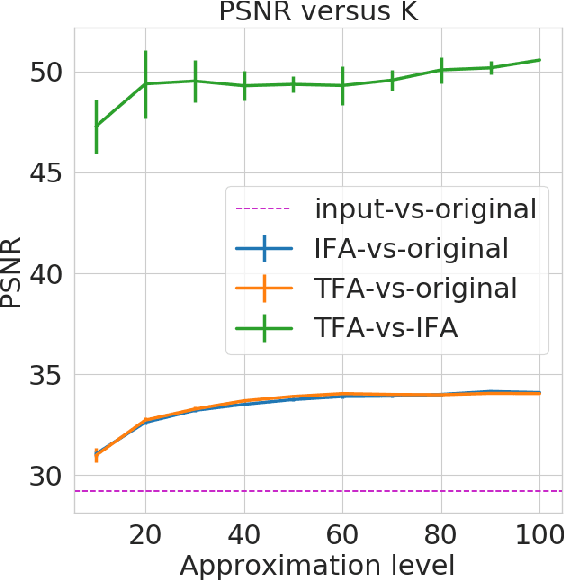
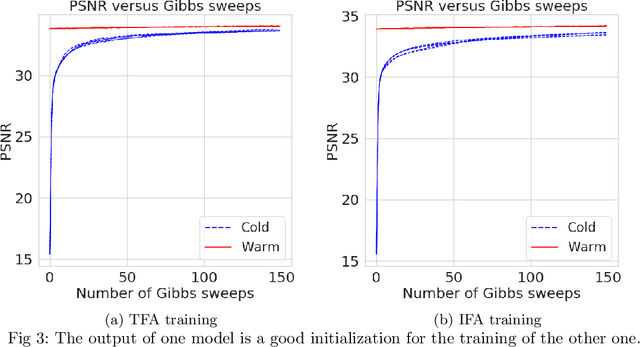
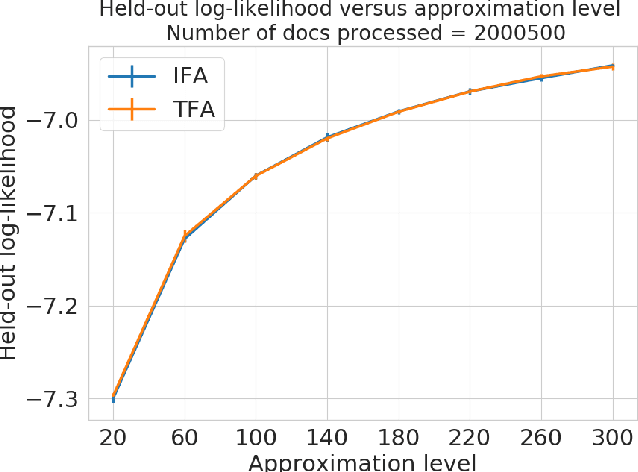
Bayesian nonparametrics based on completely random measures (CRMs) offers a flexible modeling approach when the number of clusters or latent components in a dataset is unknown. However, managing the infinite dimensionality of CRMs often leads to slow computation. Practical inference typically relies on either integrating out the infinite-dimensional parameter or using a finite approximation: a truncated finite approximation (TFA) or an independent finite approximation (IFA). The atom weights of TFAs are constructed sequentially, while the atoms of IFAs are independent, which (1) make them well-suited for parallel and distributed computation and (2) facilitates more convenient inference schemes. While IFAs have been developed in certain special cases in the past, there has not yet been a general template for construction or a systematic comparison to TFAs. We show how to construct IFAs for approximating distributions in a large family of CRMs, encompassing all those typically used in practice. We quantify the approximation error between IFAs and the target nonparametric prior, and prove that, in the worst-case, TFAs provide more component-efficient approximations than IFAs. However, in experiments on image denoising and topic modeling tasks with real data, we find that the error of Bayesian approximation methods overwhelms any finite approximation error, and IFAs perform very similarly to TFAs.

Reconstructing probabilistic trees of cellular differentiation from single-cell RNA-seq data

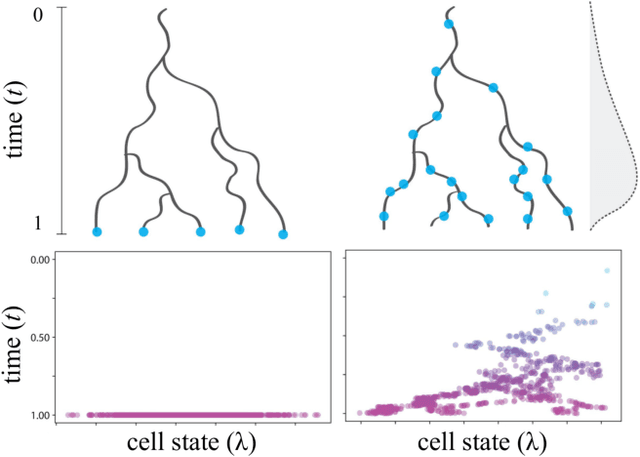
Until recently, transcriptomics was limited to bulk RNA sequencing, obscuring the underlying expression patterns of individual cells in favor of a global average. Thanks to technological advances, we can now profile gene expression across thousands or millions of individual cells in parallel. This new type of data has led to the intriguing discovery that individual cell profiles can reflect the imprint of time or dynamic processes. However, synthesizing this information to reconstruct dynamic biological phenomena from data that are noisy, heterogenous, and sparse---and from processes that may unfold asynchronously---poses a complex computational and statistical challenge. Here, we develop a full generative model for probabilistically reconstructing trees of cellular differentiation from single-cell RNA-seq data. Specifically, we extend the framework of the classical Dirichlet diffusion tree to simultaneously infer branch topology and latent cell states along continuous trajectories over the full tree. In tandem, we construct a novel Markov chain Monte Carlo sampler that interleaves Metropolis-Hastings and message passing to leverage model structure for efficient inference. Finally, we demonstrate that these techniques can recover latent trajectories from simulated single-cell transcriptomes. While this work is motivated by cellular differentiation, we derive a tractable model that provides flexible densities for any data (coupled with an appropriate noise model) that arise from continuous evolution along a latent nonparametric tree.

Fast robustness quantification with variational Bayes

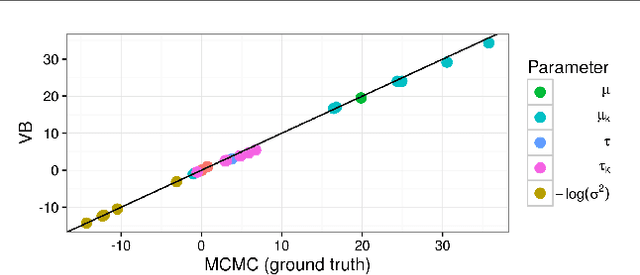
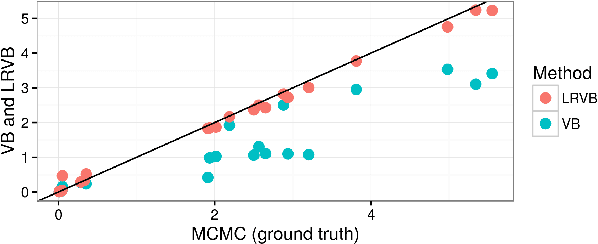
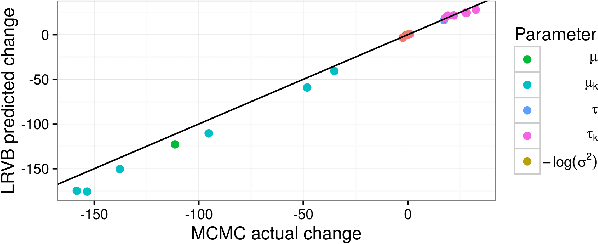
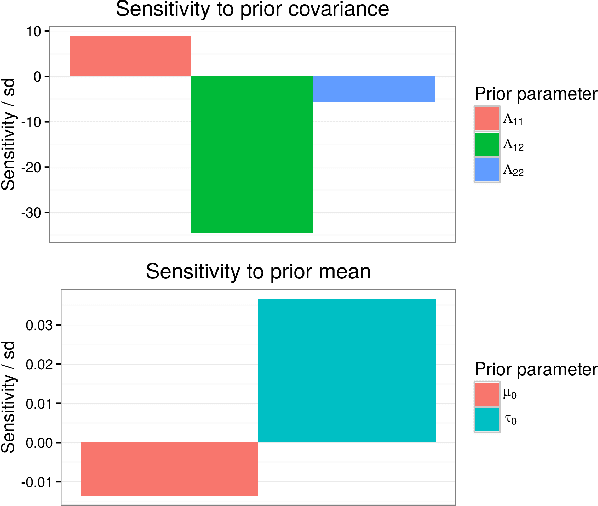
Bayesian hierarchical models are increasing popular in economics. When using hierarchical models, it is useful not only to calculate posterior expectations, but also to measure the robustness of these expectations to reasonable alternative prior choices. We use variational Bayes and linear response methods to provide fast, accurate posterior means and robustness measures with an application to measuring the effectiveness of microcredit in the developing world.