William T. Stephenson
Can we globally optimize cross-validation loss? Quasiconvexity in ridge regression
Jul 19, 2021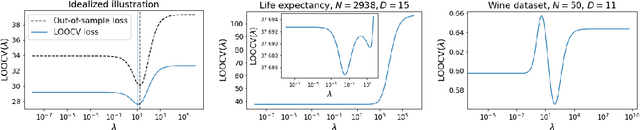
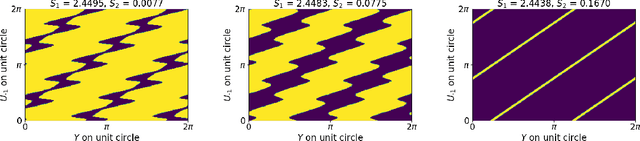
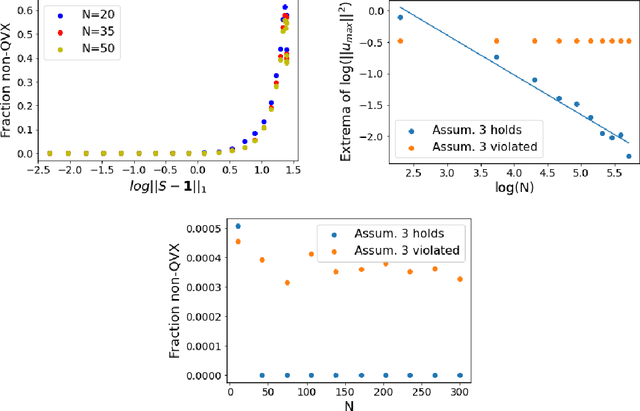
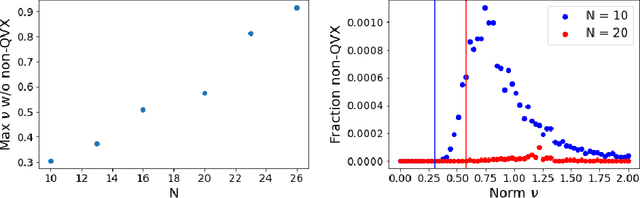
Abstract:Models like LASSO and ridge regression are extensively used in practice due to their interpretability, ease of use, and strong theoretical guarantees. Cross-validation (CV) is widely used for hyperparameter tuning in these models, but do practical optimization methods minimize the true out-of-sample loss? A recent line of research promises to show that the optimum of the CV loss matches the optimum of the out-of-sample loss (possibly after simple corrections). It remains to show how tractable it is to minimize the CV loss. In the present paper, we show that, in the case of ridge regression, the CV loss may fail to be quasiconvex and thus may have multiple local optima. We can guarantee that the CV loss is quasiconvex in at least one case: when the spectrum of the covariate matrix is nearly flat and the noise in the observed responses is not too high. More generally, we show that quasiconvexity status is independent of many properties of the observed data (response norm, covariate-matrix right singular vectors and singular-value scaling) and has a complex dependence on the few that remain. We empirically confirm our theory using simulated experiments.
Measuring the sensitivity of Gaussian processes to kernel choice
Jun 11, 2021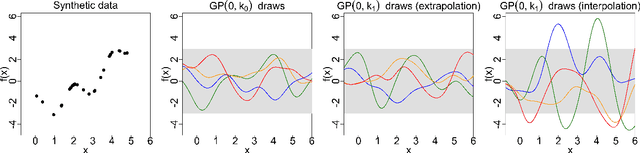
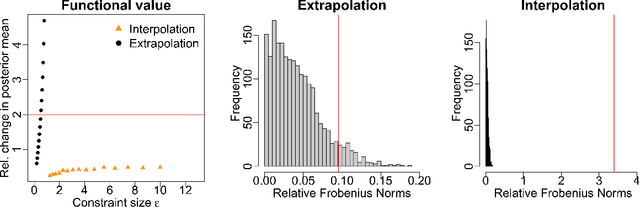
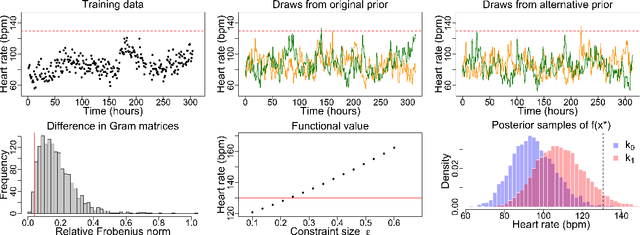
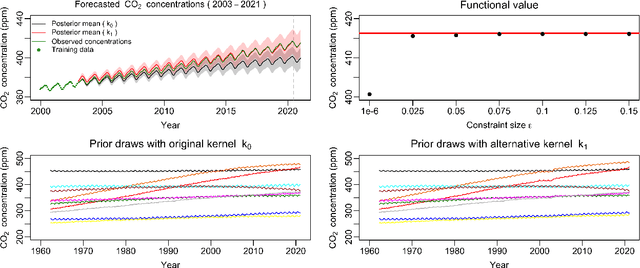
Abstract:Gaussian processes (GPs) are used to make medical and scientific decisions, including in cardiac care and monitoring of carbon dioxide emissions. But the choice of GP kernel is often somewhat arbitrary. In particular, uncountably many kernels typically align with qualitative prior knowledge (e.g. function smoothness or stationarity). But in practice, data analysts choose among a handful of convenient standard kernels (e.g. squared exponential). In the present work, we ask: Would decisions made with a GP differ under other, qualitatively interchangeable kernels? We show how to formulate this sensitivity analysis as a constrained optimization problem over a finite-dimensional space. We can then use standard optimizers to identify substantive changes in relevant decisions made with a GP. We demonstrate in both synthetic and real-world examples that decisions made with a GP can exhibit substantial sensitivity to kernel choice, even when prior draws are qualitatively interchangeable to a user.
Approximate Cross-Validation with Low-Rank Data in High Dimensions
Aug 24, 2020



Abstract:Many recent advances in machine learning are driven by a challenging trifecta: large data size $N$; high dimensions; and expensive algorithms. In this setting, cross-validation (CV) serves as an important tool for model assessment. Recent advances in approximate cross validation (ACV) provide accurate approximations to CV with only a single model fit, avoiding traditional CV's requirement for repeated runs of expensive algorithms. Unfortunately, these ACV methods can lose both speed and accuracy in high dimensions -- unless sparsity structure is present in the data. Fortunately, there is an alternative type of simplifying structure that is present in most data: approximate low rank (ALR). Guided by this observation, we develop a new algorithm for ACV that is fast and accurate in the presence of ALR data. Our first key insight is that the Hessian matrix -- whose inverse forms the computational bottleneck of existing ACV methods -- is ALR. We show that, despite our use of the \emph{inverse} Hessian, a low-rank approximation using the largest (rather than the smallest) matrix eigenvalues enables fast, reliable ACV. Our second key insight is that, in the presence of ALR data, error in existing ACV methods roughly grows with the (approximate, low) rank rather than with the (full, high) dimension. These insights allow us to prove theoretical guarantees on the quality of our proposed algorithm -- along with fast-to-compute upper bounds on its error. We demonstrate the speed and accuracy of our method, as well as the usefulness of our bounds, on a range of real and simulated data sets.
Approximate Cross-Validation for Structured Models
Jun 23, 2020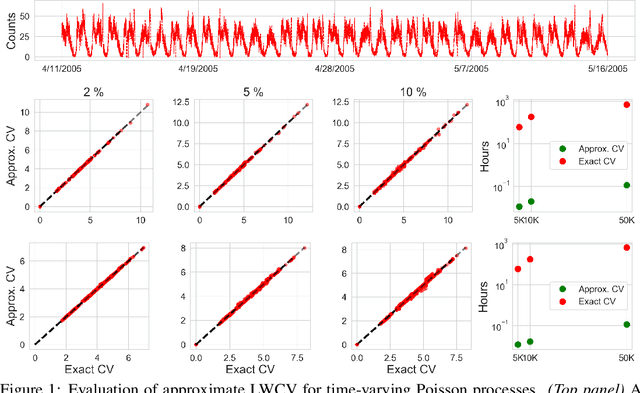
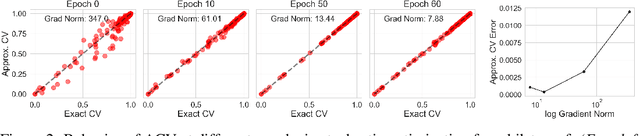
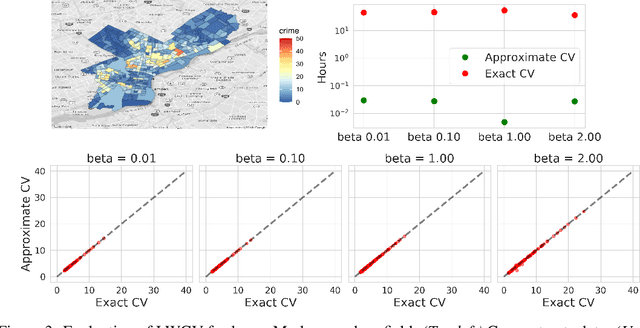
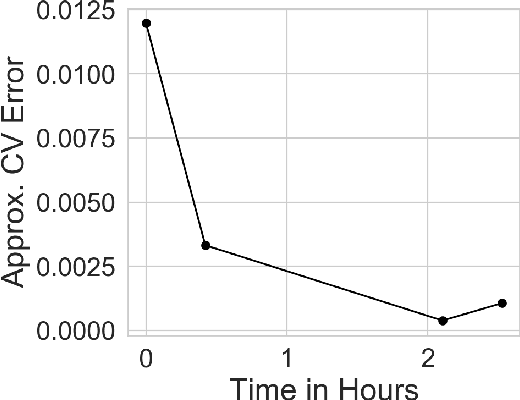
Abstract:Many modern data analyses benefit from explicitly modeling dependence structure in data -- such as measurements across time or space, ordered words in a sentence, or genes in a genome. Cross-validation is the gold standard to evaluate these analyses but can be prohibitively slow due to the need to re-run already-expensive learning algorithms many times. Previous work has shown approximate cross-validation (ACV) methods provide a fast and provably accurate alternative in the setting of empirical risk minimization. But this existing ACV work is restricted to simpler models by the assumptions that (i) data are independent and (ii) an exact initial model fit is available. In structured data analyses, (i) is always untrue, and (ii) is often untrue. In the present work, we address (i) by extending ACV to models with dependence structure. To address (ii), we verify -- both theoretically and empirically -- that ACV quality deteriorates smoothly with noise in the initial fit. We demonstrate the accuracy and computational benefits of our proposed methods on a diverse set of real-world applications.
Reconstructing probabilistic trees of cellular differentiation from single-cell RNA-seq data
Nov 28, 2018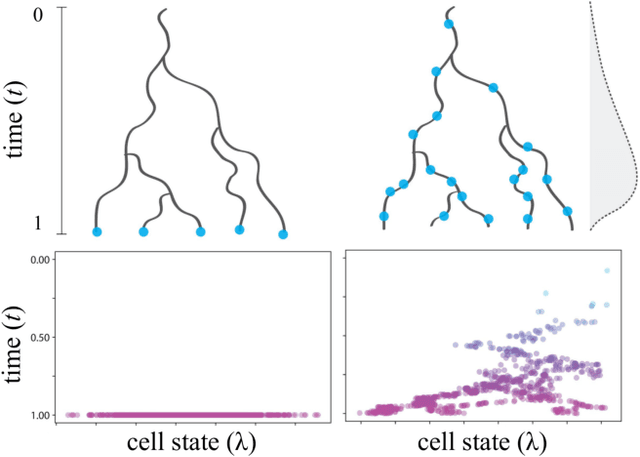



Abstract:Until recently, transcriptomics was limited to bulk RNA sequencing, obscuring the underlying expression patterns of individual cells in favor of a global average. Thanks to technological advances, we can now profile gene expression across thousands or millions of individual cells in parallel. This new type of data has led to the intriguing discovery that individual cell profiles can reflect the imprint of time or dynamic processes. However, synthesizing this information to reconstruct dynamic biological phenomena from data that are noisy, heterogenous, and sparse---and from processes that may unfold asynchronously---poses a complex computational and statistical challenge. Here, we develop a full generative model for probabilistically reconstructing trees of cellular differentiation from single-cell RNA-seq data. Specifically, we extend the framework of the classical Dirichlet diffusion tree to simultaneously infer branch topology and latent cell states along continuous trajectories over the full tree. In tandem, we construct a novel Markov chain Monte Carlo sampler that interleaves Metropolis-Hastings and message passing to leverage model structure for efficient inference. Finally, we demonstrate that these techniques can recover latent trajectories from simulated single-cell transcriptomes. While this work is motivated by cellular differentiation, we derive a tractable model that provides flexible densities for any data (coupled with an appropriate noise model) that arise from continuous evolution along a latent nonparametric tree.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge