Oblique Bayesian additive regression trees

Current implementations of Bayesian Additive Regression Trees (BART) are based on axis-aligned decision rules that recursively partition the feature space using a single feature at a time. Several authors have demonstrated that oblique trees, whose decision rules are based on linear combinations of features, can sometimes yield better predictions than axis-aligned trees and exhibit excellent theoretical properties. We develop an oblique version of BART that leverages a data-adaptive decision rule prior that recursively partitions the feature space along random hyperplanes. Using several synthetic and real-world benchmark datasets, we systematically compared our oblique BART implementation to axis-aligned BART and other tree ensemble methods, finding that oblique BART was competitive with -- and sometimes much better than -- those methods.

A Bayesian Classification Trees Approach to Treatment Effect Variation with Noncompliance

Estimating varying treatment effects in randomized trials with noncompliance is inherently challenging since variation comes from two separate sources: variation in the impact itself and variation in the compliance rate. In this setting, existing frequentist and flexible machine learning methods are highly sensitive to the weak instruments problem, in which the compliance rate is (locally) close to zero. Bayesian approaches, on the other hand, can naturally account for noncompliance via imputation. We propose a Bayesian machine learning approach that combines the best features of both approaches. Our main methodological contribution is to present a Bayesian Causal Forest model for binary response variables in scenarios with noncompliance by repeatedly imputing individuals' compliance types, allowing us to flexibly estimate varying treatment effects among compliers. Simulation studies demonstrate the usefulness of our approach when compliance and treatment effects are heterogeneous. We apply the method to detect and analyze heterogeneity in the treatment effects in the Illinois Workplace Wellness Study, which not only features heterogeneous and one-sided compliance but also several binary outcomes of interest. We demonstrate the methodology on three outcomes one year after intervention. We confirm a null effect on the presence of a chronic condition, discover meaningful heterogeneity in a "bad health" outcome that cancels out to null in classical partial effect estimates, and find substantial heterogeneity in individuals' perception of management prioritization of health and safety.

Are you using test log-likelihood correctly?

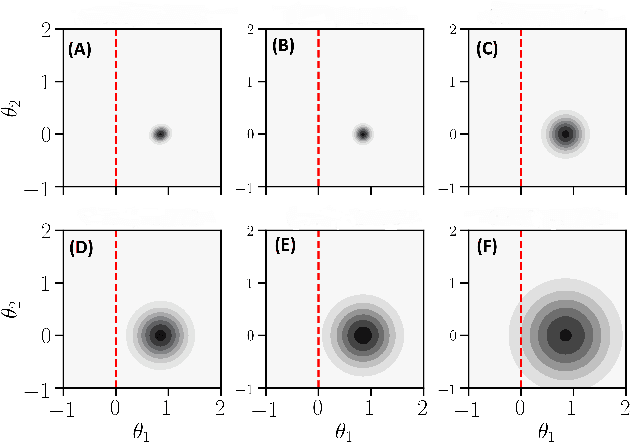
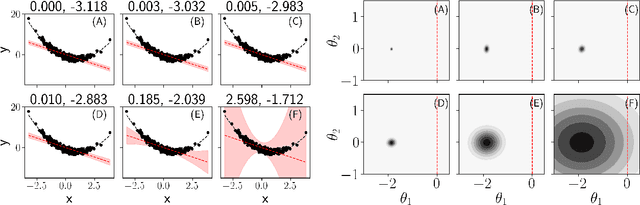
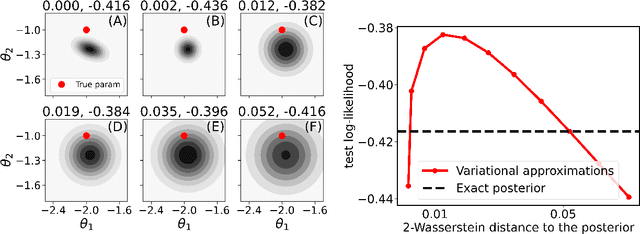
Test log-likelihood is commonly used to compare different models of the same data and different approximate inference algorithms for fitting the same probabilistic model. We present simple examples demonstrating how comparisons based on test log-likelihood can contradict comparisons according to other objectives. Specifically, our examples show that (i) conclusions about forecast accuracy based on test log-likelihood comparisons may not agree with conclusions based on other distributional quantities like means; and (ii) that approximate Bayesian inference algorithms that attain higher test log-likelihoods need not also yield more accurate posterior approximations.

A new BART prior for flexible modeling with categorical predictors

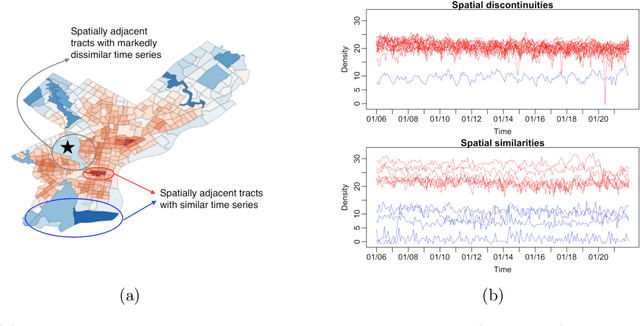
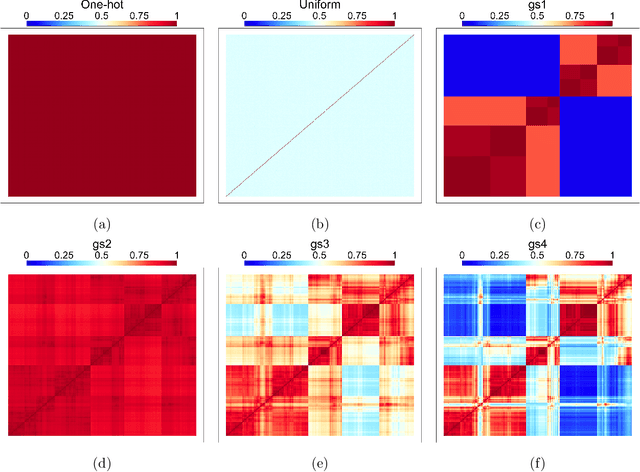
Default implementations of Bayesian Additive Regression Trees (BART) represent categorical predictors using several binary indicators, one for each level of each categorical predictor. Regression trees built with these indicators partition the levels using a ``remove one a time strategy.'' Unfortunately, the vast majority of partitions of the levels cannot be built with this strategy, severely limiting BART's ability to ``borrow strength'' across groups of levels. We overcome this limitation with a new class of regression tree and a new decision rule prior that can assign multiple levels to both the left and right child of a decision node. Motivated by spatial applications with areal data, we introduce a further decision rule prior that partitions the areas into spatially contiguous regions by deleting edges from random spanning trees of a suitably defined network. We implemented our new regression tree priors in the flexBART package, which, compared to existing implementations, often yields improved out-of-sample predictive performance without much additional computational burden. We demonstrate the efficacy of flexBART using examples from baseball and the spatiotemporal modeling of crime.

Measuring the sensitivity of Gaussian processes to kernel choice

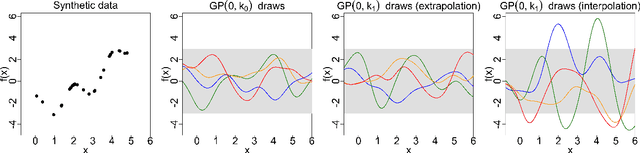
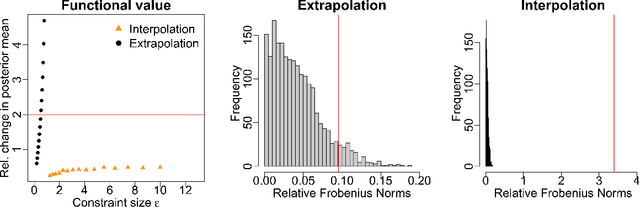
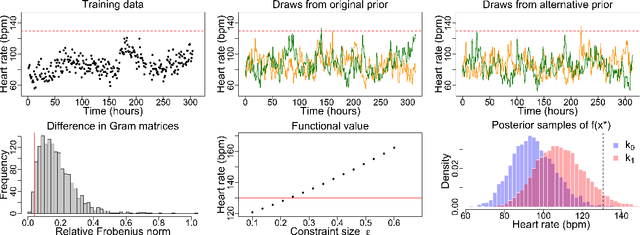
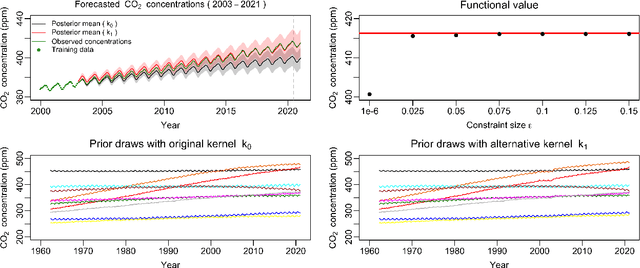
Gaussian processes (GPs) are used to make medical and scientific decisions, including in cardiac care and monitoring of carbon dioxide emissions. But the choice of GP kernel is often somewhat arbitrary. In particular, uncountably many kernels typically align with qualitative prior knowledge (e.g. function smoothness or stationarity). But in practice, data analysts choose among a handful of convenient standard kernels (e.g. squared exponential). In the present work, we ask: Would decisions made with a GP differ under other, qualitatively interchangeable kernels? We show how to formulate this sensitivity analysis as a constrained optimization problem over a finite-dimensional space. We can then use standard optimizers to identify substantive changes in relevant decisions made with a GP. We demonstrate in both synthetic and real-world examples that decisions made with a GP can exhibit substantial sensitivity to kernel choice, even when prior draws are qualitatively interchangeable to a user.

Approximate Cross-Validation for Structured Models

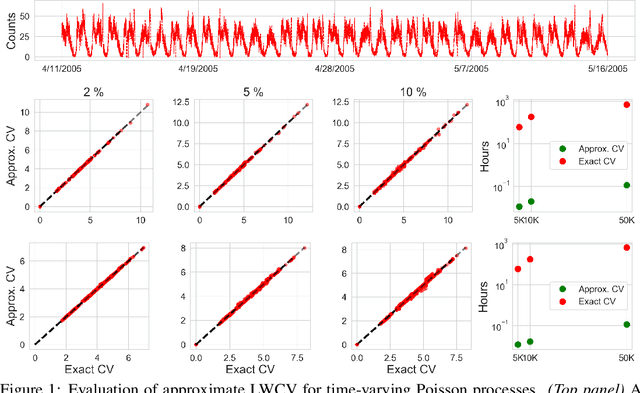
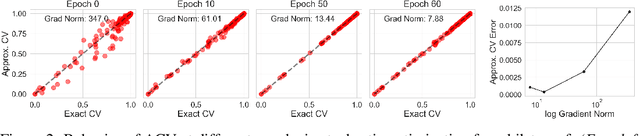
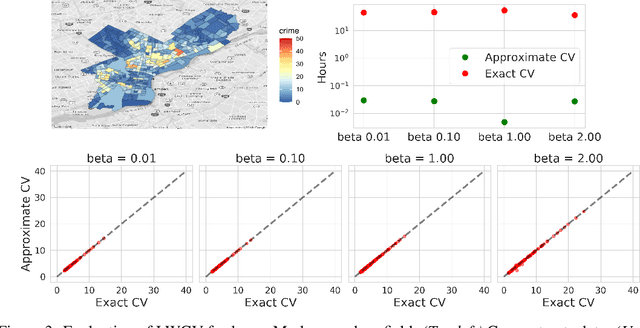
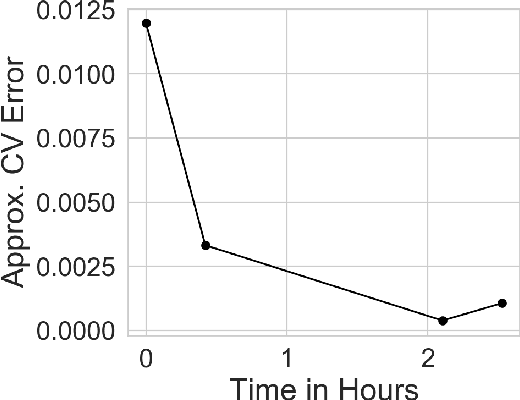
Many modern data analyses benefit from explicitly modeling dependence structure in data -- such as measurements across time or space, ordered words in a sentence, or genes in a genome. Cross-validation is the gold standard to evaluate these analyses but can be prohibitively slow due to the need to re-run already-expensive learning algorithms many times. Previous work has shown approximate cross-validation (ACV) methods provide a fast and provably accurate alternative in the setting of empirical risk minimization. But this existing ACV work is restricted to simpler models by the assumptions that (i) data are independent and (ii) an exact initial model fit is available. In structured data analyses, (i) is always untrue, and (ii) is often untrue. In the present work, we address (i) by extending ACV to models with dependence structure. To address (ii), we verify -- both theoretically and empirically -- that ACV quality deteriorates smoothly with noise in the initial fit. We demonstrate the accuracy and computational benefits of our proposed methods on a diverse set of real-world applications.