Identifying Drift, Diffusion, and Causal Structure from Temporal Snapshots

Stochastic differential equations (SDEs) are a fundamental tool for modelling dynamic processes, including gene regulatory networks (GRNs), contaminant transport, financial markets, and image generation. However, learning the underlying SDE from observational data is a challenging task, especially when individual trajectories are not observable. Motivated by burgeoning research in single-cell datasets, we present the first comprehensive approach for jointly estimating the drift and diffusion of an SDE from its temporal marginals. Assuming linear drift and additive diffusion, we prove that these parameters are identifiable from marginals if and only if the initial distribution is not invariant to a class of generalized rotations, a condition that is satisfied by most distributions. We further prove that the causal graph of any SDE with additive diffusion can be recovered from the SDE parameters. To complement this theory, we adapt entropy-regularized optimal transport to handle anisotropic diffusion, and introduce APPEX (Alternating Projection Parameter Estimation from $X_0$), an iterative algorithm designed to estimate the drift, diffusion, and causal graph of an additive noise SDE, solely from temporal marginals. We show that each of these steps are asymptotically optimal with respect to the Kullback-Leibler divergence, and demonstrate APPEX's effectiveness on simulated data from linear additive noise SDEs.

Wasserstein Mirror Gradient Flow as the limit of the Sinkhorn Algorithm

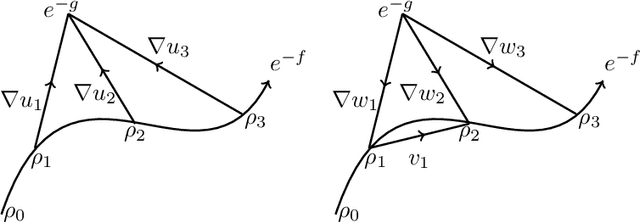
We prove that the sequence of marginals obtained from the iterations of the Sinkhorn algorithm or the iterative proportional fitting procedure (IPFP) on joint densities, converges to an absolutely continuous curve on the $2$-Wasserstein space, as the regularization parameter $\varepsilon$ goes to zero and the number of iterations is scaled as $1/\varepsilon$ (and other technical assumptions). This limit, which we call the Sinkhorn flow, is an example of a Wasserstein mirror gradient flow, a concept we introduce here inspired by the well-known Euclidean mirror gradient flows. In the case of Sinkhorn, the gradient is that of the relative entropy functional with respect to one of the marginals and the mirror is half of the squared Wasserstein distance functional from the other marginal. Interestingly, the norm of the velocity field of this flow can be interpreted as the metric derivative with respect to the linearized optimal transport (LOT) distance. An equivalent description of this flow is provided by the parabolic Monge-Amp\`{e}re PDE whose connection to the Sinkhorn algorithm was noticed by Berman (2020). We derive conditions for exponential convergence for this limiting flow. We also construct a Mckean-Vlasov diffusion whose marginal distributions follow the Sinkhorn flow.

Manifold Learning with Sparse Regularised Optimal Transport

Manifold learning is a central task in modern statistics and data science. Many datasets (cells, documents, images, molecules) can be represented as point clouds embedded in a high dimensional ambient space, however the degrees of freedom intrinsic to the data are usually far fewer than the number of ambient dimensions. The task of detecting a latent manifold along which the data are embedded is a prerequisite for a wide family of downstream analyses. Real-world datasets are subject to noisy observations and sampling, so that distilling information about the underlying manifold is a major challenge. We propose a method for manifold learning that utilises a symmetric version of optimal transport with a quadratic regularisation that constructs a sparse and adaptive affinity matrix, that can be interpreted as a generalisation of the bistochastic kernel normalisation. We prove that the resulting kernel is consistent with a Laplace-type operator in the continuous limit, establish robustness to heteroskedastic noise and exhibit these results in simulations. We identify a highly efficient computational scheme for computing this optimal transport for discrete data and demonstrate that it outperforms competing methods in a set of examples.

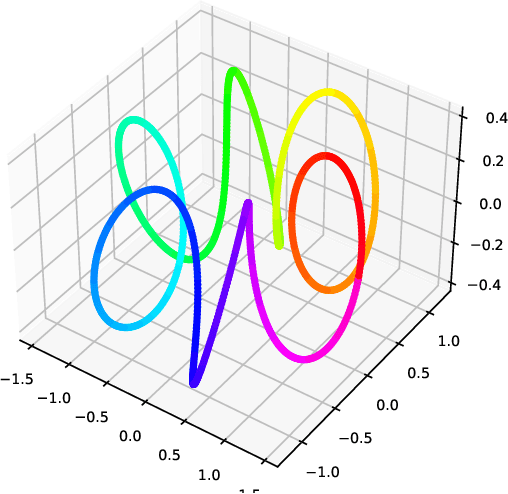
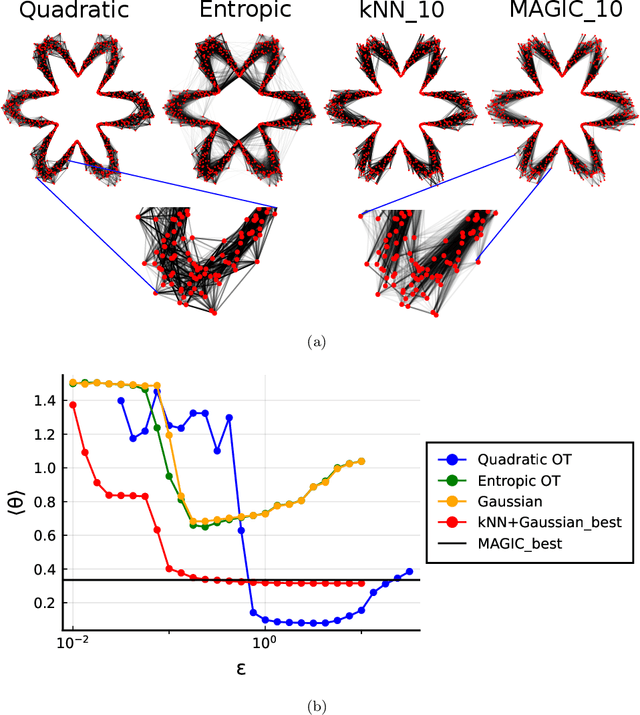
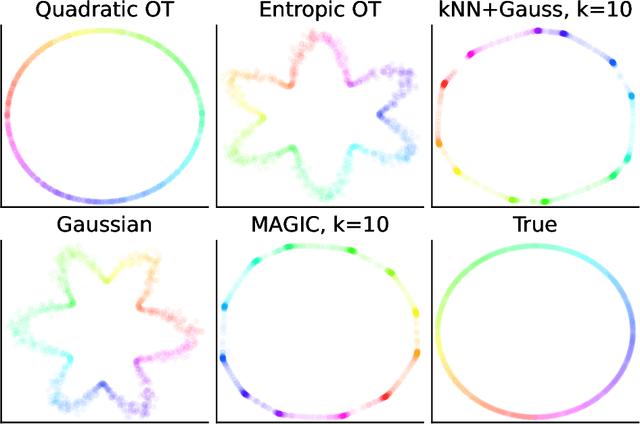
Beyond kNN: Adaptive, Sparse Neighborhood Graphs via Optimal Transport

Nearest neighbour graphs are widely used to capture the geometry or topology of a dataset. One of the most common strategies to construct such a graph is based on selecting a fixed number k of nearest neighbours (kNN) for each point. However, the kNN heuristic may become inappropriate when sampling density or noise level varies across datasets. Strategies that try to get around this typically introduce additional parameters that need to be tuned. We propose a simple approach to construct an adaptive neighbourhood graph from a single parameter, based on quadratically regularised optimal transport. Our numerical experiments show that graphs constructed in this manner perform favourably in unsupervised and semi-supervised learning applications.

Trajectory Inference via Mean-field Langevin in Path Space

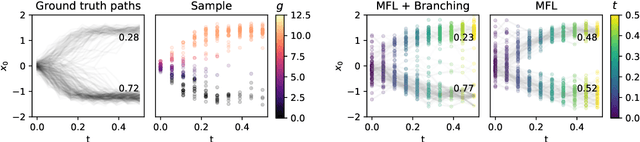
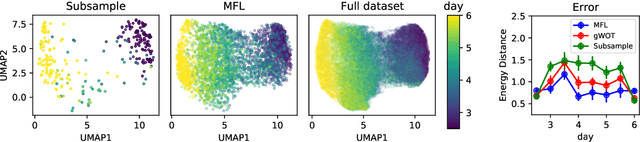
Trajectory inference aims at recovering the dynamics of a population from snapshots of its temporal marginals. To solve this task, a min-entropy estimator relative to the Wiener measure in path space was introduced by Lavenant et al. arXiv:2102.09204, and shown to consistently recover the dynamics of a large class of drift-diffusion processes from the solution of an infinite dimensional convex optimization problem. In this paper, we introduce a grid-free algorithm to compute this estimator. Our method consists in a family of point clouds (one per snapshot) coupled via Schr\"odinger bridges which evolve with noisy gradient descent. We study the mean-field limit of the dynamics and prove its global convergence at an exponential rate to the desired estimator. Overall, this leads to an inference method with end-to-end theoretical guarantees that solves an interpretable model for trajectory inference. We also present how to adapt the method to deal with mass variations, a useful extension when dealing with single cell RNA-sequencing data where cells can branch and die.

Towards a mathematical theory of trajectory inference

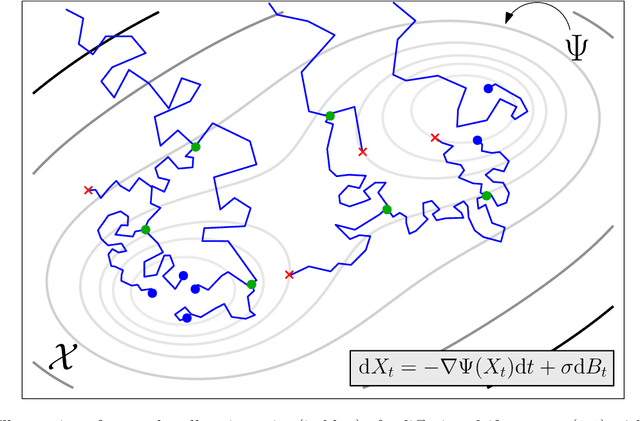
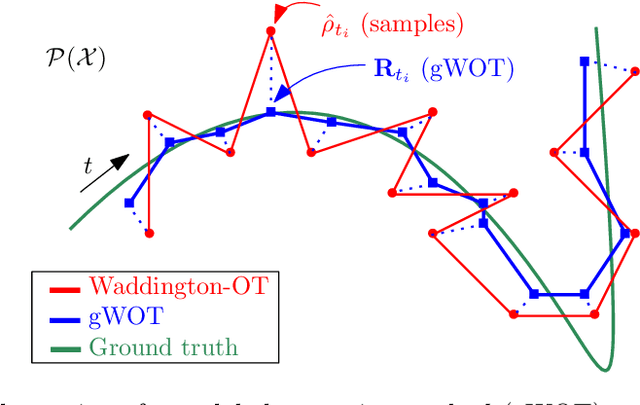
We devise a theoretical framework and a numerical method to infer trajectories of a stochastic process from snapshots of its temporal marginals. This problem arises in the analysis of single cell RNA-sequencing data, which provide high dimensional measurements of cell states but cannot track the trajectories of the cells over time. We prove that for a class of stochastic processes it is possible to recover the ground truth trajectories from limited samples of the temporal marginals at each time-point, and provide an efficient algorithm to do so in practice. The method we develop, Global Waddington-OT (gWOT), boils down to a smooth convex optimization problem posed globally over all time-points involving entropy-regularized optimal transport. We demonstrate that this problem can be solved efficiently in practice and yields good reconstructions, as we show on several synthetic and real datasets.

Reconstructing probabilistic trees of cellular differentiation from single-cell RNA-seq data

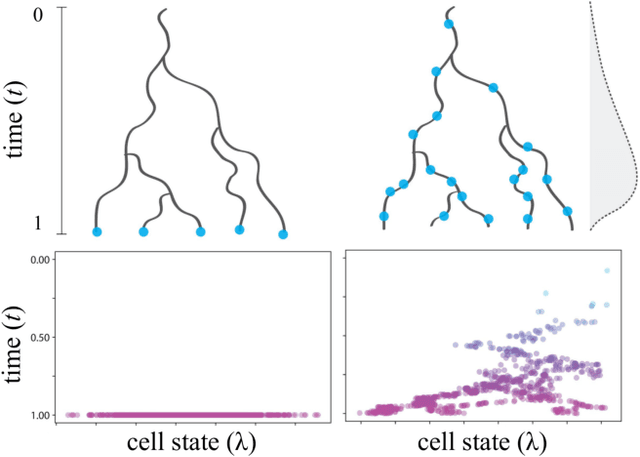
Until recently, transcriptomics was limited to bulk RNA sequencing, obscuring the underlying expression patterns of individual cells in favor of a global average. Thanks to technological advances, we can now profile gene expression across thousands or millions of individual cells in parallel. This new type of data has led to the intriguing discovery that individual cell profiles can reflect the imprint of time or dynamic processes. However, synthesizing this information to reconstruct dynamic biological phenomena from data that are noisy, heterogenous, and sparse---and from processes that may unfold asynchronously---poses a complex computational and statistical challenge. Here, we develop a full generative model for probabilistically reconstructing trees of cellular differentiation from single-cell RNA-seq data. Specifically, we extend the framework of the classical Dirichlet diffusion tree to simultaneously infer branch topology and latent cell states along continuous trajectories over the full tree. In tandem, we construct a novel Markov chain Monte Carlo sampler that interleaves Metropolis-Hastings and message passing to leverage model structure for efficient inference. Finally, we demonstrate that these techniques can recover latent trajectories from simulated single-cell transcriptomes. While this work is motivated by cellular differentiation, we derive a tractable model that provides flexible densities for any data (coupled with an appropriate noise model) that arise from continuous evolution along a latent nonparametric tree.

Statistical Optimal Transport via Factored Couplings

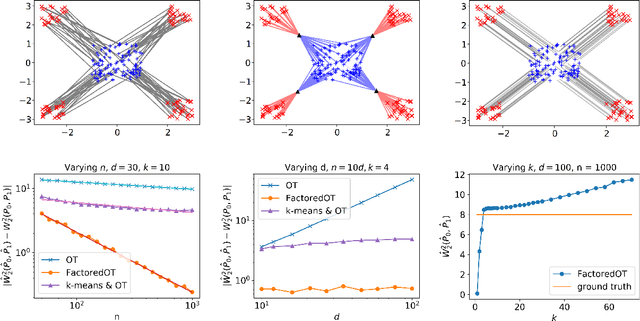
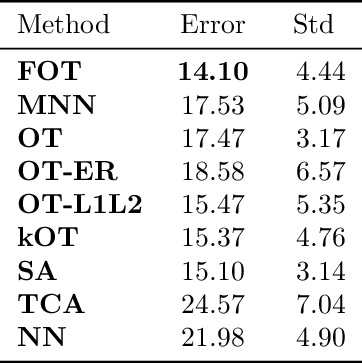
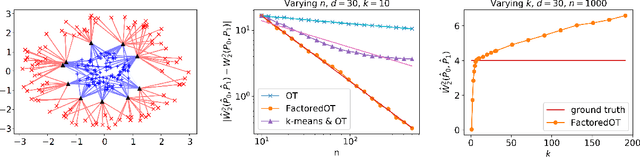
We propose a new method to estimate Wasserstein distances and optimal transport plans between two probability distributions from samples in high dimension. Unlike plug-in rules that simply replace the true distributions by their empirical counterparts, our method pro- motes couplings with low transport rank, a new structural assumption that is similar to the nonnegative rank of a matrix. Regularizing based on this assumption leads to drastic improvements on high-dimensional data for various tasks, including domain adaptation in single-cell RNA sequencing data. These findings are supported by a theoretical analysis that indicates that the transport rank is key in overcoming the curse of dimensionality inherent to data-driven optimal transport.

The geometry of kernelized spectral clustering

Clustering of data sets is a standard problem in many areas of science and engineering. The method of spectral clustering is based on embedding the data set using a kernel function, and using the top eigenvectors of the normalized Laplacian to recover the connected components. We study the performance of spectral clustering in recovering the latent labels of i.i.d. samples from a finite mixture of nonparametric distributions. The difficulty of this label recovery problem depends on the overlap between mixture components and how easily a mixture component is divided into two nonoverlapping components. When the overlap is small compared to the indivisibility of the mixture components, the principal eigenspace of the population-level normalized Laplacian operator is approximately spanned by the square-root kernelized component densities. In the finite sample setting, and under the same assumption, embedded samples from different components are approximately orthogonal with high probability when the sample size is large. As a corollary we control the fraction of samples mislabeled by spectral clustering under finite mixtures with nonparametric components.

Sharp Inequalities for $f$-divergences

$f$-divergences are a general class of divergences between probability measures which include as special cases many commonly used divergences in probability, mathematical statistics and information theory such as Kullback-Leibler divergence, chi-squared divergence, squared Hellinger distance, total variation distance etc. In this paper, we study the problem of maximizing or minimizing an $f$-divergence between two probability measures subject to a finite number of constraints on other $f$-divergences. We show that these infinite-dimensional optimization problems can all be reduced to optimization problems over small finite dimensional spaces which are tractable. Our results lead to a comprehensive and unified treatment of the problem of obtaining sharp inequalities between $f$-divergences. We demonstrate that many of the existing results on inequalities between $f$-divergences can be obtained as special cases of our results and we also improve on some existing non-sharp inequalities.