Monge-Kantorovich Fitting With Sobolev Budgets

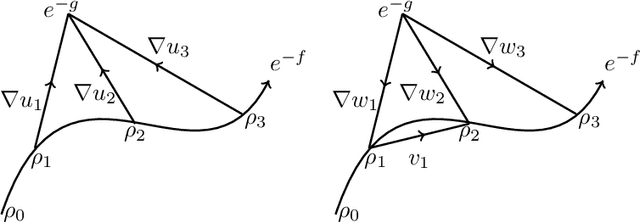
We consider the problem of finding the ``best'' approximation of an $n$-dimensional probability measure $\rho$ using a measure $\nu$ whose support is parametrized by $f : \mathbb{R}^m \to \mathbb{R}^n$ where $m < n$. We quantify the performance of the approximation with the Monge-Kantorovich $p$-cost (also called the Wasserstein $p$-cost) $\mathbb{W}_p^p(\rho, \nu)$, and constrain the complexity of the approximation by bounding the $W^{k,q}$ Sobolev norm of $f$, which acts as a ``budget.'' We may then reformulate the problem as minimizing a functional $\mathscr{J}_p(f)$ under a constraint on the Sobolev budget. We treat general $k \geq 1$ for the Sobolev differentiability order (though $q, m$ are chosen to restrict $W^{k,q}$ to the supercritical regime $k q > m$ to guarantee existence of optimizers). The problem is closely related to (but distinct from) principal curves with length constraints when $m=1, k = 1$ and smoothing splines when $k > 1$. New aspects and challenges arise from the higher order differentiability condition. We study the gradient of $\mathscr{J}_p$, which is given by a vector field along $f$ we call the barycenter field. We use it to construct improvements to a given $f$, which gives a nontrivial (almost) strict monotonicty relation between the functional $\mathscr{J}_p$ and the Sobolev budget. We also provide a natural discretization scheme and establish its consistency. We use this scheme to model a generative learning task; in particular, we demonstrate that adding a constraint like ours as a soft penalty yields substantial improvement in training a GAN to produce images of handwritten digits, with performance competitive with weight-decay.

Wasserstein Mirror Gradient Flow as the limit of the Sinkhorn Algorithm

We prove that the sequence of marginals obtained from the iterations of the Sinkhorn algorithm or the iterative proportional fitting procedure (IPFP) on joint densities, converges to an absolutely continuous curve on the $2$-Wasserstein space, as the regularization parameter $\varepsilon$ goes to zero and the number of iterations is scaled as $1/\varepsilon$ (and other technical assumptions). This limit, which we call the Sinkhorn flow, is an example of a Wasserstein mirror gradient flow, a concept we introduce here inspired by the well-known Euclidean mirror gradient flows. In the case of Sinkhorn, the gradient is that of the relative entropy functional with respect to one of the marginals and the mirror is half of the squared Wasserstein distance functional from the other marginal. Interestingly, the norm of the velocity field of this flow can be interpreted as the metric derivative with respect to the linearized optimal transport (LOT) distance. An equivalent description of this flow is provided by the parabolic Monge-Amp\`{e}re PDE whose connection to the Sinkhorn algorithm was noticed by Berman (2020). We derive conditions for exponential convergence for this limiting flow. We also construct a Mckean-Vlasov diffusion whose marginal distributions follow the Sinkhorn flow.

Towards a mathematical theory of trajectory inference

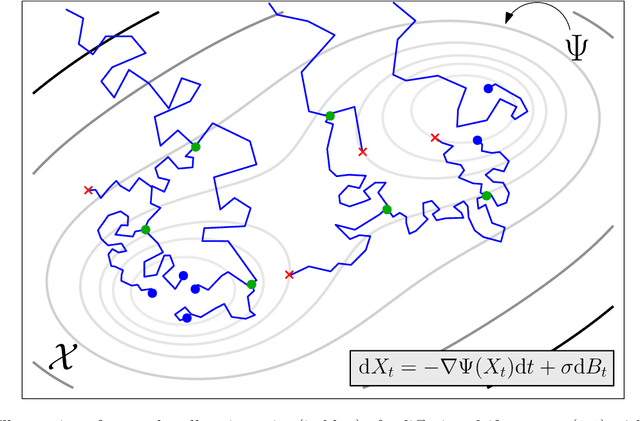
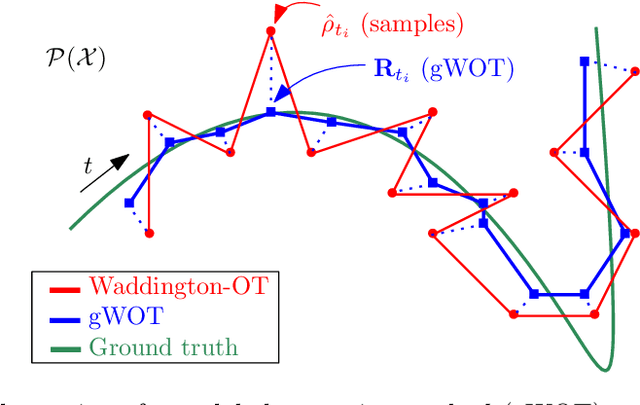
We devise a theoretical framework and a numerical method to infer trajectories of a stochastic process from snapshots of its temporal marginals. This problem arises in the analysis of single cell RNA-sequencing data, which provide high dimensional measurements of cell states but cannot track the trajectories of the cells over time. We prove that for a class of stochastic processes it is possible to recover the ground truth trajectories from limited samples of the temporal marginals at each time-point, and provide an efficient algorithm to do so in practice. The method we develop, Global Waddington-OT (gWOT), boils down to a smooth convex optimization problem posed globally over all time-points involving entropy-regularized optimal transport. We demonstrate that this problem can be solved efficiently in practice and yields good reconstructions, as we show on several synthetic and real datasets.