The Benefits of Balance: From Information Projections to Variance Reduction

Data balancing across multiple modalities/sources appears in various forms in several foundation models (e.g., CLIP and DINO) achieving universal representation learning. We show that this iterative algorithm, usually used to avoid representation collapse, enjoys an unsuspected benefit: reducing the variance of estimators that are functionals of the empirical distribution over these sources. We provide non-asymptotic bounds quantifying this variance reduction effect and relate them to the eigendecays of appropriately defined Markov operators. We explain how various forms of data balancing in contrastive multimodal learning and self-supervised clustering can be interpreted as instances of this variance reduction scheme.

Iterated Schrödinger bridge approximation to Wasserstein Gradient Flows

We introduce a novel discretization scheme for Wasserstein gradient flows that involves successively computing Schr\"{o}dinger bridges with the same marginals. This is different from both the forward/geodesic approximation and the backward/Jordan-Kinderlehrer-Otto (JKO) approximations. The proposed scheme has two advantages: one, it avoids the use of the score function, and, two, it is amenable to particle-based approximations using the Sinkhorn algorithm. Our proof hinges upon showing that relative entropy between the Schr\"{o}dinger bridge with the same marginals at temperature $\epsilon$ and the joint distribution of a stationary Langevin diffusion at times zero and $\epsilon$ is of the order $o(\epsilon^2)$ with an explicit dependence given by Fisher information. Owing to this inequality, we can show, using a triangular approximation argument, that the interpolated iterated application of the Schr\"{o}dinger bridge approximation converge to the Wasserstein gradient flow, for a class of gradient flows, including the heat flow. The results also provide a probabilistic and rigorous framework for the convergence of the self-attention mechanisms in transformer networks to the solutions of heat flows, first observed in the inspiring work SABP22 in machine learning research.

Projected Langevin dynamics and a gradient flow for entropic optimal transport

The classical (overdamped) Langevin dynamics provide a natural algorithm for sampling from its invariant measure, which uniquely minimizes an energy functional over the space of probability measures, and which concentrates around the minimizer(s) of the associated potential when the noise parameter is small. We introduce analogous diffusion dynamics that sample from an entropy-regularized optimal transport, which uniquely minimizes the same energy functional but constrained to the set $\Pi(\mu,\nu)$ of couplings of two given marginal probability measures $\mu$ and $\nu$ on $\mathbb{R}^d$, and which concentrates around the optimal transport coupling(s) for small regularization parameter. More specifically, our process satisfies two key properties: First, the law of the solution at each time stays in $\Pi(\mu,\nu)$ if it is initialized there. Second, the long-time limit is the unique solution of an entropic optimal transport problem. In addition, we show by means of a new log-Sobolev-type inequality that the convergence holds exponentially fast, for sufficiently large regularization parameter and for a class of marginals which strictly includes all strongly log-concave measures. By studying the induced Wasserstein geometry of the submanifold $\Pi(\mu,\nu)$, we argue that the SDE can be viewed as a Wasserstein gradient flow on this space of couplings, at least when $d=1$, and we identify a conjectural gradient flow for $d \ge 2$. The main technical difficulties stems from the appearance of conditional expectation terms which serve to constrain the dynamics to $\Pi(\mu,\nu)$.

Path convergence of Markov chains on large graphs

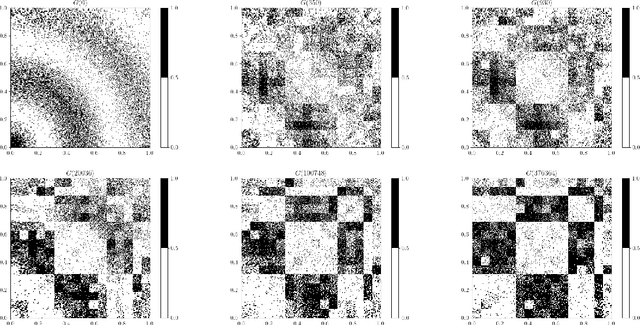
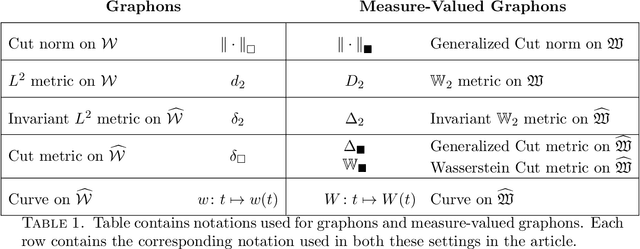
We consider two classes of natural stochastic processes on finite unlabeled graphs. These are Euclidean stochastic optimization algorithms on the adjacency matrix of weighted graphs and a modified version of the Metropolis MCMC algorithm on stochastic block models over unweighted graphs. In both cases we show that, as the size of the graph goes to infinity, the random trajectories of the stochastic processes converge to deterministic limits. These deterministic limits are curves on the space of measure-valued graphons. Measure-valued graphons, introduced by Lov\'{a}sz and Szegedy, are a refinement of the concept of graphons that can distinguish between two infinite exchangeable arrays that give rise to the same graphon limit. We introduce new metrics on this space which provide us with a natural notion of convergence for our limit theorems. This notion is equivalent to the convergence of infinite-exchangeable arrays. Under a suitable time-scaling, the Metropolis chain admits a diffusion limit as the number of vertices go to infinity. We then demonstrate that, in an appropriately formulated zero-noise limit, the stochastic process of adjacency matrices of this diffusion converge to a deterministic gradient flow curve on the space of graphons introduced in arXiv:2111.09459 [math.PR]. Under suitable assumptions, this allows us to estimate an exponential convergence rate for the Metropolis chain in a certain limiting regime. To the best of our knowledge, both the actual rate and the connection between a natural Metropolis chain commonly used in exponential random graph models and gradient flows on graphons are new in the literature.

Wasserstein Mirror Gradient Flow as the limit of the Sinkhorn Algorithm

We prove that the sequence of marginals obtained from the iterations of the Sinkhorn algorithm or the iterative proportional fitting procedure (IPFP) on joint densities, converges to an absolutely continuous curve on the $2$-Wasserstein space, as the regularization parameter $\varepsilon$ goes to zero and the number of iterations is scaled as $1/\varepsilon$ (and other technical assumptions). This limit, which we call the Sinkhorn flow, is an example of a Wasserstein mirror gradient flow, a concept we introduce here inspired by the well-known Euclidean mirror gradient flows. In the case of Sinkhorn, the gradient is that of the relative entropy functional with respect to one of the marginals and the mirror is half of the squared Wasserstein distance functional from the other marginal. Interestingly, the norm of the velocity field of this flow can be interpreted as the metric derivative with respect to the linearized optimal transport (LOT) distance. An equivalent description of this flow is provided by the parabolic Monge-Amp\`{e}re PDE whose connection to the Sinkhorn algorithm was noticed by Berman (2020). We derive conditions for exponential convergence for this limiting flow. We also construct a Mckean-Vlasov diffusion whose marginal distributions follow the Sinkhorn flow.

Stochastic optimization on matrices and a graphon McKean-Vlasov limit

We consider stochastic gradient descents on the space of large symmetric matrices of suitable functions that are invariant under permuting the rows and columns using the same permutation. We establish deterministic limits of these random curves as the dimensions of the matrices go to infinity while the entries remain bounded. Under a ``small noise'' assumption the limit is shown to be the gradient flow of functions on graphons whose existence was established in arXiv:2111.09459. We also consider limits of stochastic gradient descents with added properly scaled reflected Brownian noise. The limiting curve of graphons is characterized by a family of stochastic differential equations with reflections and can be thought of as an extension of the classical McKean-Vlasov limit for interacting diffusions. The proofs introduce a family of infinite-dimensional exchangeable arrays of reflected diffusions and a novel notion of propagation of chaos for large matrices of interacting diffusions.

Triangular Flows for Generative Modeling: Statistical Consistency, Smoothness Classes, and Fast Rates

Triangular flows, also known as Kn\"{o}the-Rosenblatt measure couplings, comprise an important building block of normalizing flow models for generative modeling and density estimation, including popular autoregressive flow models such as real-valued non-volume preserving transformation models (Real NVP). We present statistical guarantees and sample complexity bounds for triangular flow statistical models. In particular, we establish the statistical consistency and the finite sample convergence rates of the Kullback-Leibler estimator of the Kn\"{o}the-Rosenblatt measure coupling using tools from empirical process theory. Our results highlight the anisotropic geometry of function classes at play in triangular flows, shed light on optimal coordinate ordering, and lead to statistical guarantees for Jacobian flows. We conduct numerical experiments on synthetic data to illustrate the practical implications of our theoretical findings.

Entropy Regularized Optimal Transport Independence Criterion

Optimal transport (OT) and its entropy regularized offspring have recently gained a lot of attention in both machine learning and AI domains. In particular, optimal transport has been used to develop probability metrics between probability distributions. We introduce in this paper an independence criterion based on entropy regularized optimal transport. Our criterion can be used to test for independence between two samples. We establish non-asymptotic bounds for our test statistic, and study its statistical behavior under both the null and alternative hypothesis. Our theoretical results involve tools from U-process theory and optimal transport theory. We present experimental results on existing benchmarks, illustrating the interest of the proposed criterion.

Gradient flows on graphons: existence, convergence, continuity equations

Wasserstein gradient flows on probability measures have found a host of applications in various optimization problems. They typically arise as the continuum limit of exchangeable particle systems evolving by some mean-field interaction involving a gradient-type potential. However, in many problems, such as in multi-layer neural networks, the so-called particles are edge weights on large graphs whose nodes are exchangeable. Such large graphs are known to converge to continuum limits called graphons as their size grow to infinity. We show that the Euclidean gradient flow of a suitable function of the edge-weights converges to a novel continuum limit given by a curve on the space of graphons that can be appropriately described as a gradient flow or, more technically, a curve of maximal slope. Several natural functions on graphons, such as homomorphism functions and the scalar entropy, are covered by our set-up, and the examples have been worked out in detail.

Asymptotics of Entropy-Regularized Optimal Transport via Chaos Decomposition

Consider the problem of estimating the optimal coupling (i.e., matching) between $N$ i.i.d. data points sampled from two densities $\rho_0$ and $\rho_1$ in $\mathbb{R}^d$. The cost of transport is an arbitrary continuous function that satisfies suitable growth and integrability assumptions. For both computational efficiency and smoothness, often a regularization term using entropy is added to this discrete problem. We introduce a modification of the commonly used discrete entropic regularization (Cuturi '13) such that the optimal coupling for the regularized problem can be thought of as the static Schr\"odinger bridge with $N$ particles. This paper is on the asymptotic properties of this discrete Schr\"odinger bridge as $N$ tends to infinity. We show that it converges to the continuum Schr\"odinger bridge and derive the first two error terms of orders $N^{-1/2}$ and $N^{-1}$, respectively. This gives us functional CLT, including for the cost of transport, and second order Gaussian chaos limits when the limiting Gaussian variance is zero, extending similar recent results derived for finite state spaces and the quadratic cost. The proofs are based on a novel chaos decomposition of the discrete Schr\"odinger bridge by polynomial functions of the pair of empirical distributions as a first and second order Taylor approximations in the space of measures. This is achieved by extending the Hoeffding decomposition from the classical theory of U-statistics. The kernels corresponding to the first and second order chaoses are given by Markov operators which have natural interpretations in the Sinkhorn algorithm.