The Benefits of Balance: From Information Projections to Variance Reduction

Data balancing across multiple modalities/sources appears in various forms in several foundation models (e.g., CLIP and DINO) achieving universal representation learning. We show that this iterative algorithm, usually used to avoid representation collapse, enjoys an unsuspected benefit: reducing the variance of estimators that are functionals of the empirical distribution over these sources. We provide non-asymptotic bounds quantifying this variance reduction effect and relate them to the eigendecays of appropriately defined Markov operators. We explain how various forms of data balancing in contrastive multimodal learning and self-supervised clustering can be interpreted as instances of this variance reduction scheme.

Confidence Sets under Generalized Self-Concordance

This paper revisits a fundamental problem in statistical inference from a non-asymptotic theoretical viewpoint $\unicode{x2013}$ the construction of confidence sets. We establish a finite-sample bound for the estimator, characterizing its asymptotic behavior in a non-asymptotic fashion. An important feature of our bound is that its dimension dependency is captured by the effective dimension $\unicode{x2013}$ the trace of the limiting sandwich covariance $\unicode{x2013}$ which can be much smaller than the parameter dimension in some regimes. We then illustrate how the bound can be used to obtain a confidence set whose shape is adapted to the optimization landscape induced by the loss function. Unlike previous works that rely heavily on the strong convexity of the loss function, we only assume the Hessian is lower bounded at optimum and allow it to gradually becomes degenerate. This property is formalized by the notion of generalized self-concordance which originated from convex optimization. Moreover, we demonstrate how the effective dimension can be estimated from data and characterize its estimation accuracy. We apply our results to maximum likelihood estimation with generalized linear models, score matching with exponential families, and hypothesis testing with Rao's score test.

MAUVE Scores for Generative Models: Theory and Practice

Generative AI has matured to a point where large-scale models can generate text that seems indistinguishable from human-written text and remarkably photorealistic images. Automatically measuring how close the distribution of generated data is to the target real data distribution is a key step in diagnosing existing models and developing better models. We present MAUVE, a family of comparison measures between pairs of distributions such as those encountered in the generative modeling of text or images. These scores are statistical summaries of divergence frontiers capturing two types of errors in generative modeling. We explore four approaches to statistically estimate these scores: vector quantization, non-parametric estimation, classifier-based estimation, and parametric Gaussian approximations. We provide statistical bounds for the vector quantization approach. Empirically, we find that the proposed scores paired with a range of $f$-divergences and statistical estimation methods can quantify the gaps between the distributions of human-written text and those of modern neural language models by correlating with human judgments and identifying known properties of the generated texts. We conclude the paper by demonstrating its applications to other AI domains and discussing practical recommendations.

Stochastic Optimization for Spectral Risk Measures

Spectral risk objectives - also called $L$-risks - allow for learning systems to interpolate between optimizing average-case performance (as in empirical risk minimization) and worst-case performance on a task. We develop stochastic algorithms to optimize these quantities by characterizing their subdifferential and addressing challenges such as biasedness of subgradient estimates and non-smoothness of the objective. We show theoretically and experimentally that out-of-the-box approaches such as stochastic subgradient and dual averaging are hindered by bias and that our approach outperforms them.

Statistical and Computational Guarantees for Influence Diagnostics

Influence diagnostics such as influence functions and approximate maximum influence perturbations are popular in machine learning and in AI domain applications. Influence diagnostics are powerful statistical tools to identify influential datapoints or subsets of datapoints. We establish finite-sample statistical bounds, as well as computational complexity bounds, for influence functions and approximate maximum influence perturbations using efficient inverse-Hessian-vector product implementations. We illustrate our results with generalized linear models and large attention based models on synthetic and real data.

Orthogonal Statistical Learning with Self-Concordant Loss

Orthogonal statistical learning and double machine learning have emerged as general frameworks for two-stage statistical prediction in the presence of a nuisance component. We establish non-asymptotic bounds on the excess risk of orthogonal statistical learning methods with a loss function satisfying a self-concordance property. Our bounds improve upon existing bounds by a dimension factor while lifting the assumption of strong convexity. We illustrate the results with examples from multiple treatment effect estimation and generalized partially linear modeling.

Distribution Embedding Networks for Meta-Learning with Heterogeneous Covariate Spaces

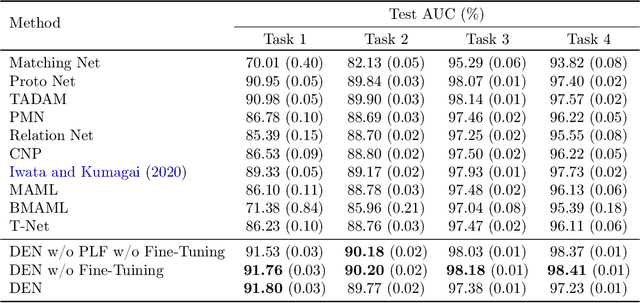
We propose Distribution Embedding Networks (DEN) for classification with small data using meta-learning techniques. Unlike existing meta-learning approaches that focus on image recognition tasks and require the training and target tasks to be similar, DEN is specifically designed to be trained on a diverse set of training tasks and applied on tasks whose number and distribution of covariates differ vastly from its training tasks. Such property of DEN is enabled by its three-block architecture: a covariate transformation block followed by a distribution embedding block and then a classification block. We provide theoretical insights to show that this architecture allows the embedding and classification blocks to be fixed after pre-training on a diverse set of tasks; only the covariate transformation block with relatively few parameters needs to be updated for each new task. To facilitate the training of DEN, we also propose an approach to synthesize binary classification training tasks, and demonstrate that DEN outperforms existing methods in a number of synthetic and real tasks in numerical studies.

Entropy Regularized Optimal Transport Independence Criterion

Optimal transport (OT) and its entropy regularized offspring have recently gained a lot of attention in both machine learning and AI domains. In particular, optimal transport has been used to develop probability metrics between probability distributions. We introduce in this paper an independence criterion based on entropy regularized optimal transport. Our criterion can be used to test for independence between two samples. We establish non-asymptotic bounds for our test statistic, and study its statistical behavior under both the null and alternative hypothesis. Our theoretical results involve tools from U-process theory and optimal transport theory. We present experimental results on existing benchmarks, illustrating the interest of the proposed criterion.

Score-Based Change Detection for Gradient-Based Learning Machines

The widespread use of machine learning algorithms calls for automatic change detection algorithms to monitor their behavior over time. As a machine learning algorithm learns from a continuous, possibly evolving, stream of data, it is desirable and often critical to supplement it with a companion change detection algorithm to facilitate its monitoring and control. We present a generic score-based change detection method that can detect a change in any number of components of a machine learning model trained via empirical risk minimization. This proposed statistical hypothesis test can be readily implemented for such models designed within a differentiable programming framework. We establish the consistency of the hypothesis test and show how to calibrate it to achieve a prescribed false alarm rate. We illustrate the versatility of the approach on synthetic and real data.

Divergence Frontiers for Generative Models: Sample Complexity, Quantization Level, and Frontier Integral

The spectacular success of deep generative models calls for quantitative tools to measure their statistical performance. Divergence frontiers have recently been proposed as an evaluation framework for generative models, due to their ability to measure the quality-diversity trade-off inherent to deep generative modeling. However, the statistical behavior of divergence frontiers estimated from data remains unknown to this day. In this paper, we establish non-asymptotic bounds on the sample complexity of the plug-in estimator of divergence frontiers. Along the way, we introduce a novel integral summary of divergence frontiers. We derive the corresponding non-asymptotic bounds and discuss the choice of the quantization level by balancing the two types of approximation errors arisen from its computation. We also augment the divergence frontier framework by investigating the statistical performance of smoothed distribution estimators such as the Good-Turing estimator. We illustrate the theoretical results with numerical examples from natural language processing and computer vision.