Distribution Embedding Networks for Meta-Learning with Heterogeneous Covariate Spaces

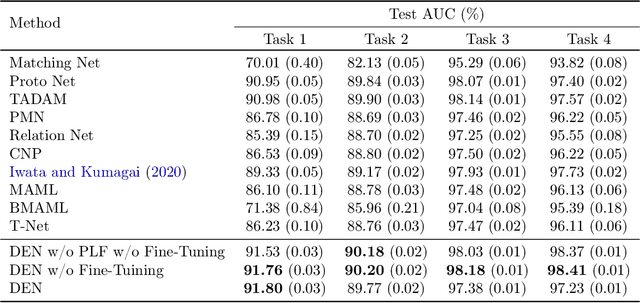
We propose Distribution Embedding Networks (DEN) for classification with small data using meta-learning techniques. Unlike existing meta-learning approaches that focus on image recognition tasks and require the training and target tasks to be similar, DEN is specifically designed to be trained on a diverse set of training tasks and applied on tasks whose number and distribution of covariates differ vastly from its training tasks. Such property of DEN is enabled by its three-block architecture: a covariate transformation block followed by a distribution embedding block and then a classification block. We provide theoretical insights to show that this architecture allows the embedding and classification blocks to be fixed after pre-training on a diverse set of tasks; only the covariate transformation block with relatively few parameters needs to be updated for each new task. To facilitate the training of DEN, we also propose an approach to synthesize binary classification training tasks, and demonstrate that DEN outperforms existing methods in a number of synthetic and real tasks in numerical studies.