Distribution Embedding Networks for Meta-Learning with Heterogeneous Covariate Spaces

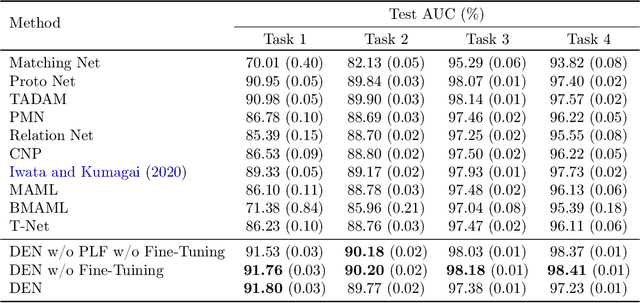
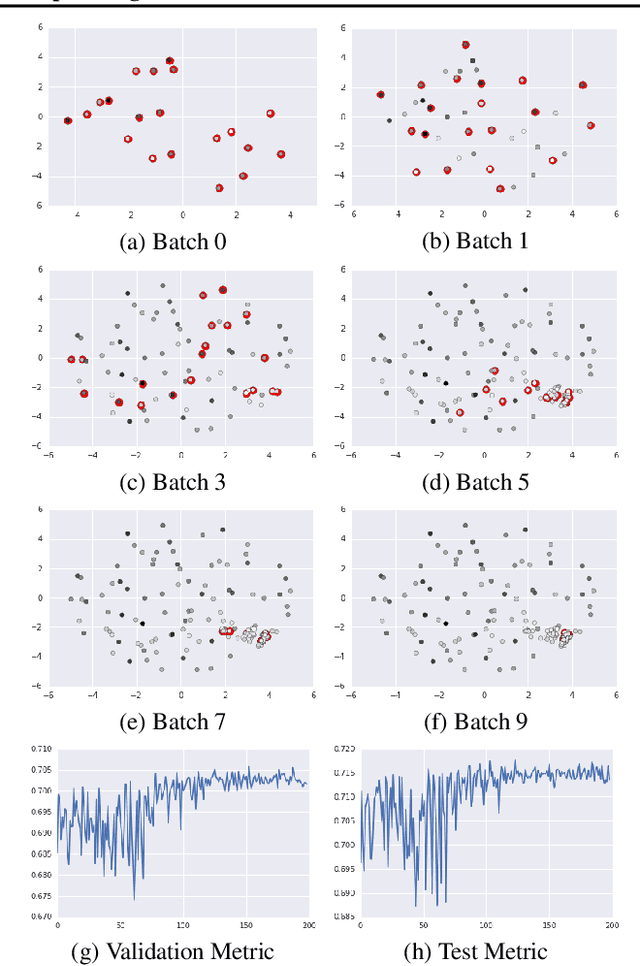
We propose Distribution Embedding Networks (DEN) for classification with small data using meta-learning techniques. Unlike existing meta-learning approaches that focus on image recognition tasks and require the training and target tasks to be similar, DEN is specifically designed to be trained on a diverse set of training tasks and applied on tasks whose number and distribution of covariates differ vastly from its training tasks. Such property of DEN is enabled by its three-block architecture: a covariate transformation block followed by a distribution embedding block and then a classification block. We provide theoretical insights to show that this architecture allows the embedding and classification blocks to be fixed after pre-training on a diverse set of tasks; only the covariate transformation block with relatively few parameters needs to be updated for each new task. To facilitate the training of DEN, we also propose an approach to synthesize binary classification training tasks, and demonstrate that DEN outperforms existing methods in a number of synthetic and real tasks in numerical studies.

Optimizing Black-box Metrics with Iterative Example Weighting

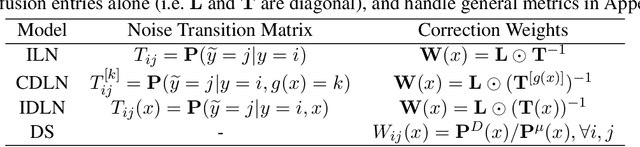
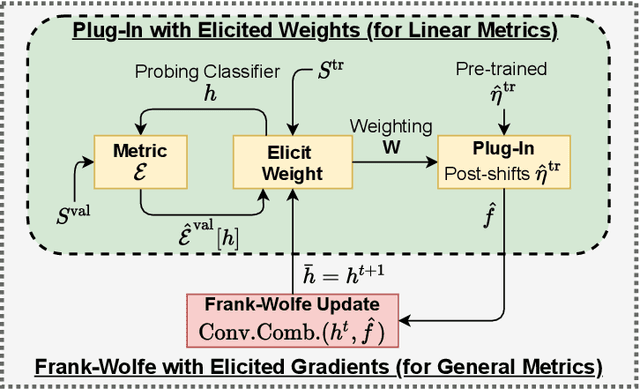
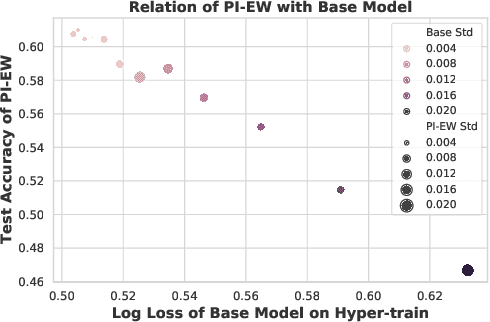
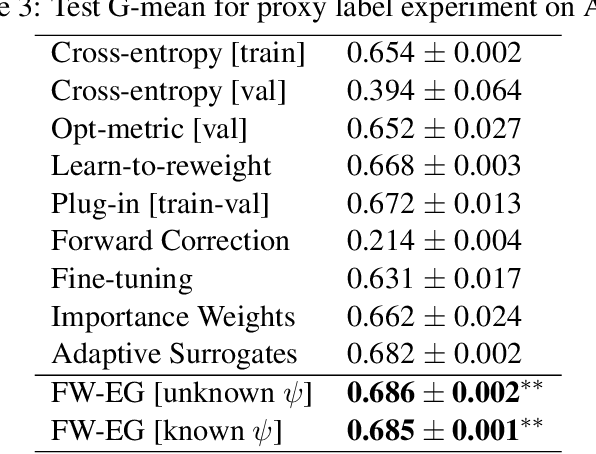
We consider learning to optimize a classification metric defined by a black-box function of the confusion matrix. Such black-box learning settings are ubiquitous, for example, when the learner only has query access to the metric of interest, or in noisy-label and domain adaptation applications where the learner must evaluate the metric via performance evaluation using a small validation sample. Our approach is to adaptively learn example weights on the training dataset such that the resulting weighted objective best approximates the metric on the validation sample. We show how to model and estimate the example weights and use them to iteratively post-shift a pre-trained class probability estimator to construct a classifier. We also analyze the resulting procedure's statistical properties. Experiments on various label noise, domain shift, and fair classification setups confirm that our proposal is better than the individual state-of-the-art baselines for each application.

Optimizing Black-box Metrics with Adaptive Surrogates

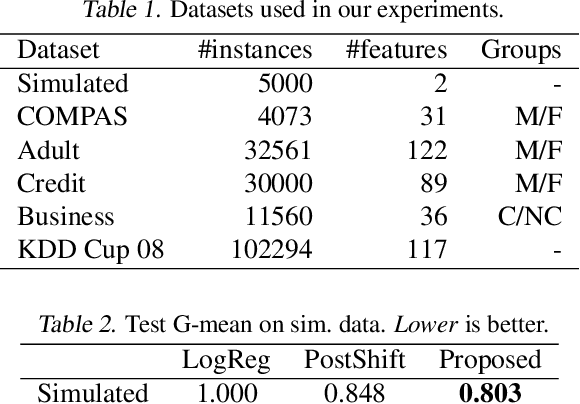
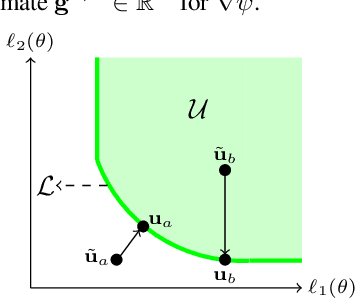
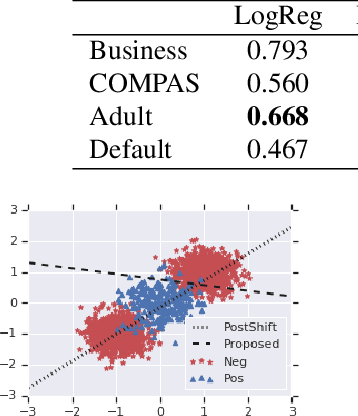
We address the problem of training models with black-box and hard-to-optimize metrics by expressing the metric as a monotonic function of a small number of easy-to-optimize surrogates. We pose the training problem as an optimization over a relaxed surrogate space, which we solve by estimating local gradients for the metric and performing inexact convex projections. We analyze gradient estimates based on finite differences and local linear interpolations, and show convergence of our approach under smoothness assumptions with respect to the surrogates. Experimental results on classification and ranking problems verify the proposal performs on par with methods that know the mathematical formulation, and adds notable value when the form of the metric is unknown.

Proxy Fairness

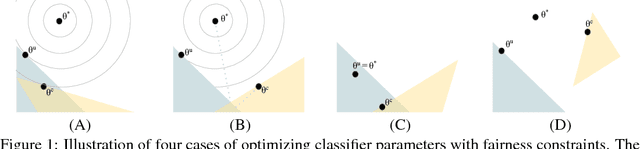
We consider the problem of improving fairness when one lacks access to a dataset labeled with protected groups, making it difficult to take advantage of strategies that can improve fairness but require protected group labels, either at training or runtime. To address this, we investigate improving fairness metrics for proxy groups, and test whether doing so results in improved fairness for the true sensitive groups. Results on benchmark and real-world datasets demonstrate that such a proxy fairness strategy can work well in practice. However, we caution that the effectiveness likely depends on the choice of fairness metric, as well as how aligned the proxy groups are with the true protected groups in terms of the constrained model parameters.

Metric-Optimized Example Weights

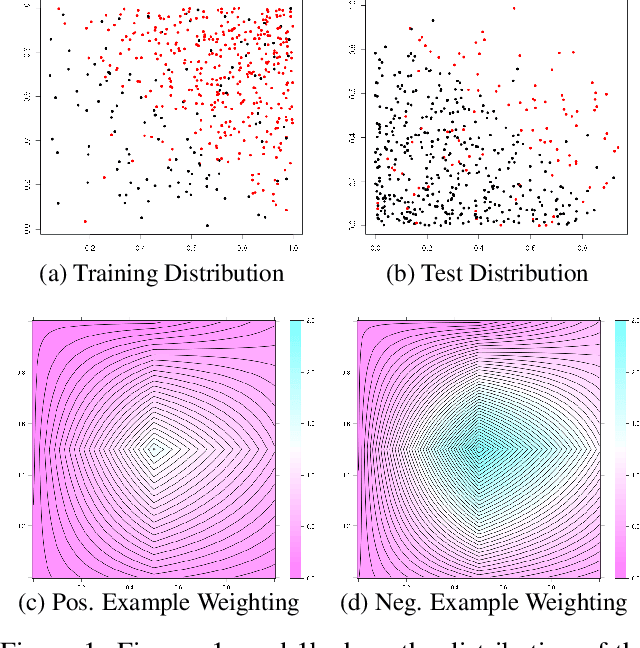
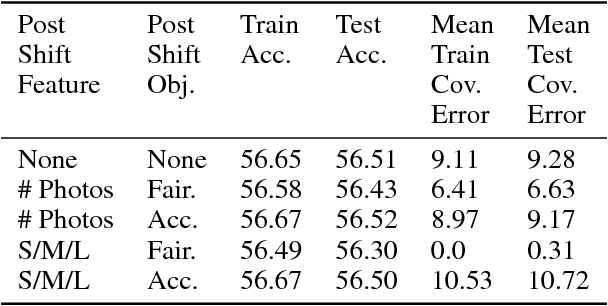
Real-world machine learning applications often have complex test metrics, and may have training and test data that follow different distributions. We propose addressing these issues by using a weighted loss function with a standard convex loss, but with weights on the training examples that are learned to optimize the test metric of interest on the validation set. These metric-optimized example weights can be learned for any test metric, including black box losses and customized metrics for specific applications. We illustrate the performance of our proposal with public benchmark datasets and real-world applications with domain shift and custom loss functions that balance multiple objectives, impose fairness policies, and are non-convex and non-decomposable.

Efficient Learning and Planning with Compressed Predictive States

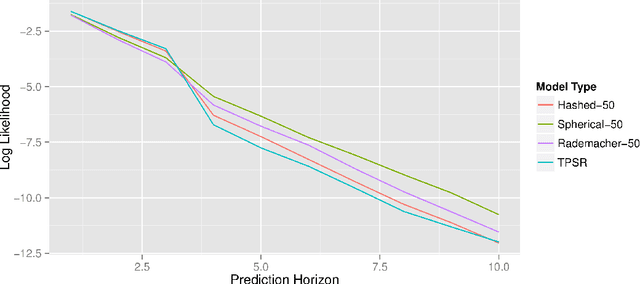
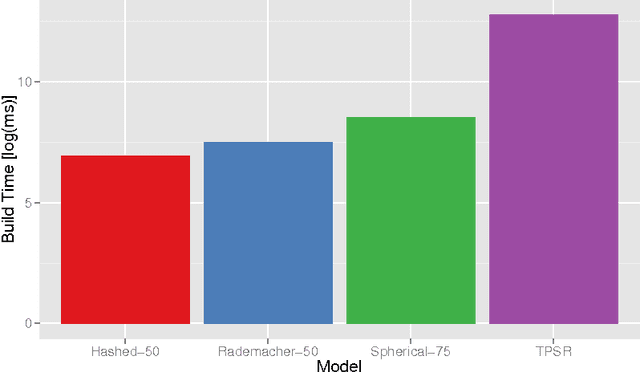
Predictive state representations (PSRs) offer an expressive framework for modelling partially observable systems. By compactly representing systems as functions of observable quantities, the PSR learning approach avoids using local-minima prone expectation-maximization and instead employs a globally optimal moment-based algorithm. Moreover, since PSRs do not require a predetermined latent state structure as an input, they offer an attractive framework for model-based reinforcement learning when agents must plan without a priori access to a system model. Unfortunately, the expressiveness of PSRs comes with significant computational cost, and this cost is a major factor inhibiting the use of PSRs in applications. In order to alleviate this shortcoming, we introduce the notion of compressed PSRs (CPSRs). The CPSR learning approach combines recent advancements in dimensionality reduction, incremental matrix decomposition, and compressed sensing. We show how this approach provides a principled avenue for learning accurate approximations of PSRs, drastically reducing the computational costs associated with learning while also providing effective regularization. Going further, we propose a planning framework which exploits these learned models. And we show that this approach facilitates model-learning and planning in large complex partially observable domains, a task that is infeasible without the principled use of compression.

Non-Deterministic Policies in Markovian Decision Processes

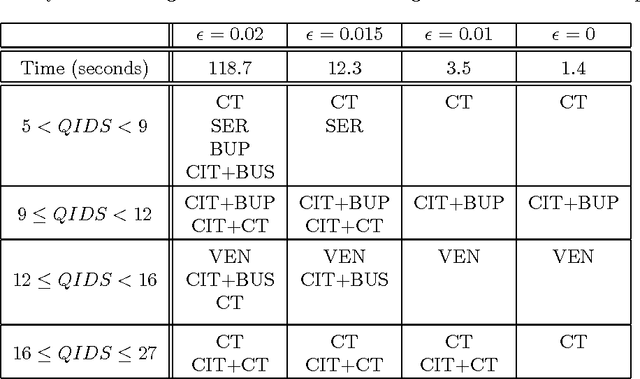
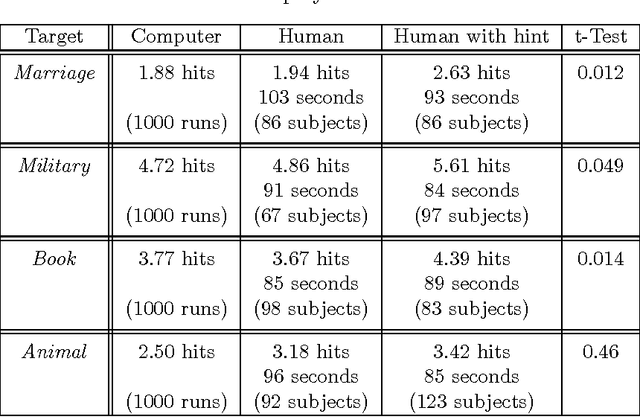
Markovian processes have long been used to model stochastic environments. Reinforcement learning has emerged as a framework to solve sequential planning and decision-making problems in such environments. In recent years, attempts were made to apply methods from reinforcement learning to construct decision support systems for action selection in Markovian environments. Although conventional methods in reinforcement learning have proved to be useful in problems concerning sequential decision-making, they cannot be applied in their current form to decision support systems, such as those in medical domains, as they suggest policies that are often highly prescriptive and leave little room for the users input. Without the ability to provide flexible guidelines, it is unlikely that these methods can gain ground with users of such systems. This paper introduces the new concept of non-deterministic policies to allow more flexibility in the users decision-making process, while constraining decisions to remain near optimal solutions. We provide two algorithms to compute non-deterministic policies in discrete domains. We study the output and running time of these method on a set of synthetic and real-world problems. In an experiment with human subjects, we show that humans assisted by hints based on non-deterministic policies outperform both human-only and computer-only agents in a web navigation task.

Bellman Error Based Feature Generation using Random Projections on Sparse Spaces

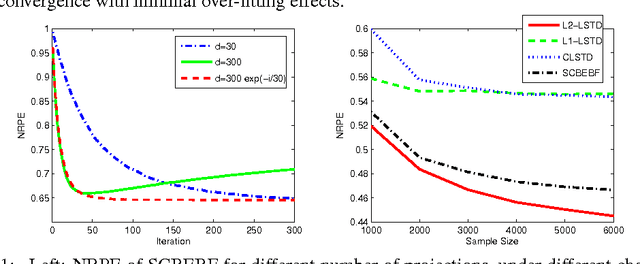
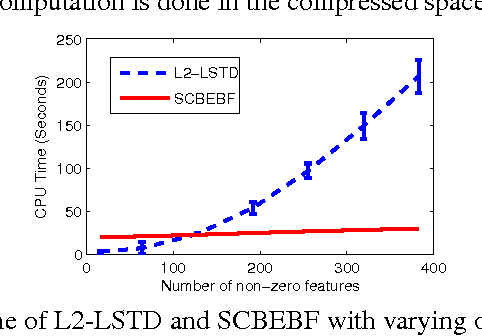
We address the problem of automatic generation of features for value function approximation. Bellman Error Basis Functions (BEBFs) have been shown to improve the error of policy evaluation with function approximation, with a convergence rate similar to that of value iteration. We propose a simple, fast and robust algorithm based on random projections to generate BEBFs for sparse feature spaces. We provide a finite sample analysis of the proposed method, and prove that projections logarithmic in the dimension of the original space are enough to guarantee contraction in the error. Empirical results demonstrate the strength of this method.