Bipartite Ranking From Multiple Labels: On Loss Versus Label Aggregation

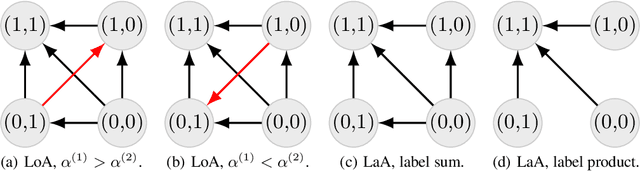
Bipartite ranking is a fundamental supervised learning problem, with the goal of learning a ranking over instances with maximal area under the ROC curve (AUC) against a single binary target label. However, one may often observe multiple binary target labels, e.g., from distinct human annotators. How can one synthesize such labels into a single coherent ranking? In this work, we formally analyze two approaches to this problem -- loss aggregation and label aggregation -- by characterizing their Bayes-optimal solutions. Based on this, we show that while both methods can yield Pareto-optimal solutions, loss aggregation can exhibit label dictatorship: one can inadvertently (and undesirably) favor one label over others. This suggests that label aggregation can be preferable to loss aggregation, which we empirically verify.

Universal Model Routing for Efficient LLM Inference

Large language models' significant advances in capabilities are accompanied by significant increases in inference costs. Model routing is a simple technique for reducing inference cost, wherein one maintains a pool of candidate LLMs, and learns to route each prompt to the smallest feasible LLM. Existing works focus on learning a router for a fixed pool of LLMs. In this paper, we consider the problem of dynamic routing, where new, previously unobserved LLMs are available at test time. We propose a new approach to this problem that relies on representing each LLM as a feature vector, derived based on predictions on a set of representative prompts. Based on this, we detail two effective strategies, relying on cluster-based routing and a learned cluster map respectively. We prove that these strategies are estimates of a theoretically optimal routing rule, and provide an excess risk bound to quantify their errors. Experiments on a range of public benchmarks show the effectiveness of the proposed strategies in routing amongst more than 30 unseen LLMs.

Cascade-Aware Training of Language Models

Reducing serving cost and latency is a fundamental concern for the deployment of language models (LMs) in business applications. To address this, cascades of LMs offer an effective solution that conditionally employ smaller models for simpler queries. Cascaded systems are typically built with independently trained models, neglecting the advantages of considering inference-time interactions of the cascaded LMs during training. In this paper, we present cascade-aware training(CAT), an approach to optimizing the overall quality-cost performance tradeoff of a cascade of LMs. We achieve inference-time benefits by training the small LM with awareness of its place in a cascade and downstream capabilities. We demonstrate the value of the proposed method with over 60 LM tasks of the SuperGLUE, WMT22, and FLAN2021 datasets.

Faster Cascades via Speculative Decoding

Cascades and speculative decoding are two common approaches to improving language models' inference efficiency. Both approaches involve interleaving models of different sizes, but via fundamentally distinct mechanisms: cascades employ a deferral rule that invokes the larger model only for "hard" inputs, while speculative decoding uses speculative execution to primarily invoke the larger model in parallel verification mode. These mechanisms offer different benefits: empirically, cascades are often capable of yielding better quality than even the larger model, while theoretically, speculative decoding offers a guarantee of quality-neutrality. In this paper, we leverage the best of both these approaches by designing new speculative cascading techniques that implement their deferral rule through speculative execution. We characterize the optimal deferral rule for our speculative cascades, and employ a plug-in approximation to the optimal rule. Through experiments with T5 models on benchmark language tasks, we show that the proposed approach yields better cost-quality trade-offs than cascading and speculative decoding baselines.

Language Model Cascades: Token-level uncertainty and beyond

Recent advances in language models (LMs) have led to significant improvements in quality on complex NLP tasks, but at the expense of increased inference costs. Cascading offers a simple strategy to achieve more favorable cost-quality tradeoffs: here, a small model is invoked for most "easy" instances, while a few "hard" instances are deferred to the large model. While the principles underpinning cascading are well-studied for classification tasks - with deferral based on predicted class uncertainty favored theoretically and practically - a similar understanding is lacking for generative LM tasks. In this work, we initiate a systematic study of deferral rules for LM cascades. We begin by examining the natural extension of predicted class uncertainty to generative LM tasks, namely, the predicted sequence uncertainty. We show that this measure suffers from the length bias problem, either over- or under-emphasizing outputs based on their lengths. This is because LMs produce a sequence of uncertainty values, one for each output token; and moreover, the number of output tokens is variable across examples. To mitigate this issue, we propose to exploit the richer token-level uncertainty information implicit in generative LMs. We argue that naive predicted sequence uncertainty corresponds to a simple aggregation of these uncertainties. By contrast, we show that incorporating token-level uncertainty through learned post-hoc deferral rules can significantly outperform such simple aggregation strategies, via experiments on a range of natural language benchmarks with FLAN-T5 models. We further show that incorporating embeddings from the smaller model and intermediate layers of the larger model can give an additional boost in the overall cost-quality tradeoff.

Metric-aware LLM inference

Large language models (LLMs) have demonstrated strong results on a range of NLP tasks. Typically, outputs are obtained via autoregressive sampling from the LLM's underlying distribution. We show that this inference strategy can be suboptimal for a range of tasks and associated evaluation metrics. As a remedy, we propose metric aware LLM inference: a decision theoretic approach optimizing for custom metrics at inference time. We report improvements over baselines on academic benchmarks and publicly available models.

Distributionally Robust Post-hoc Classifiers under Prior Shifts

The generalization ability of machine learning models degrades significantly when the test distribution shifts away from the training distribution. We investigate the problem of training models that are robust to shifts caused by changes in the distribution of class-priors or group-priors. The presence of skewed training priors can often lead to the models overfitting to spurious features. Unlike existing methods, which optimize for either the worst or the average performance over classes or groups, our work is motivated by the need for finer control over the robustness properties of the model. We present an extremely lightweight post-hoc approach that performs scaling adjustments to predictions from a pre-trained model, with the goal of minimizing a distributionally robust loss around a chosen target distribution. These adjustments are computed by solving a constrained optimization problem on a validation set and applied to the model during test time. Our constrained optimization objective is inspired by a natural notion of robustness to controlled distribution shifts. Our method comes with provable guarantees and empirically makes a strong case for distributional robust post-hoc classifiers. An empirical implementation is available at https://github.com/weijiaheng/Drops.

When Does Confidence-Based Cascade Deferral Suffice?

Cascades are a classical strategy to enable inference cost to vary adaptively across samples, wherein a sequence of classifiers are invoked in turn. A deferral rule determines whether to invoke the next classifier in the sequence, or to terminate prediction. One simple deferral rule employs the confidence of the current classifier, e.g., based on the maximum predicted softmax probability. Despite being oblivious to the structure of the cascade -- e.g., not modelling the errors of downstream models -- such confidence-based deferral often works remarkably well in practice. In this paper, we seek to better understand the conditions under which confidence-based deferral may fail, and when alternate deferral strategies can perform better. We first present a theoretical characterisation of the optimal deferral rule, which precisely characterises settings under which confidence-based deferral may suffer. We then study post-hoc deferral mechanisms, and demonstrate they can significantly improve upon confidence-based deferral in settings where (i) downstream models are specialists that only work well on a subset of inputs, (ii) samples are subject to label noise, and (iii) there is distribution shift between the train and test set.

Learning to reject meets OOD detection: Are all abstentions created equal?

Learning to reject (L2R) and out-of-distribution (OOD) detection are two classical problems, each of which involve detecting certain abnormal samples: in L2R, the goal is to detect "hard" samples on which to abstain, while in OOD detection, the goal is to detect "outlier" samples not drawn from the training distribution. Intriguingly, despite being developed in parallel literatures, both problems share a simple baseline: the maximum softmax probability (MSP) score. However, there is limited understanding of precisely how these problems relate. In this paper, we formally relate these problems, and show how they may be jointly solved. We first show that while MSP is theoretically optimal for L2R, it can be theoretically sub-optimal for OOD detection in some important practical settings. We then characterize the Bayes-optimal classifier for a unified formulation that generalizes both L2R and OOD detection. Based on this, we design a plug-in approach for learning to abstain on both inlier and OOD samples, while constraining the total abstention budget. Experiments on benchmark OOD datasets demonstrate that our approach yields competitive classification and OOD detection performance compared to baselines from both literatures.

Consistent Multiclass Algorithms for Complex Metrics and Constraints

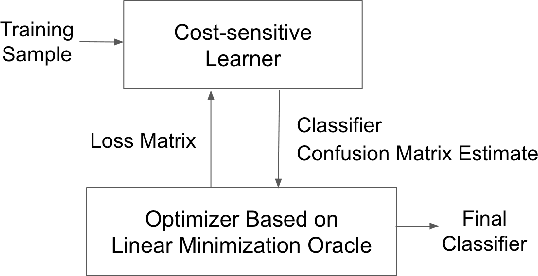
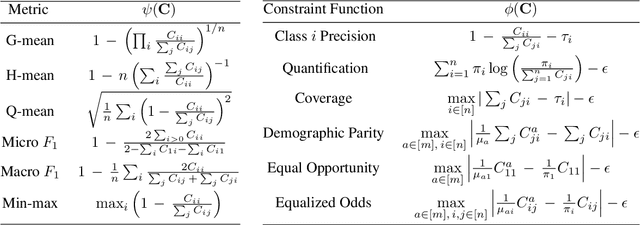
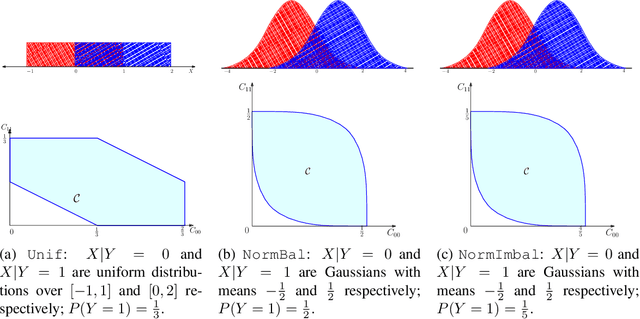
We present consistent algorithms for multiclass learning with complex performance metrics and constraints, where the objective and constraints are defined by arbitrary functions of the confusion matrix. This setting includes many common performance metrics such as the multiclass G-mean and micro F1-measure, and constraints such as those on the classifier's precision and recall and more recent measures of fairness discrepancy. We give a general framework for designing consistent algorithms for such complex design goals by viewing the learning problem as an optimization problem over the set of feasible confusion matrices. We provide multiple instantiations of our framework under different assumptions on the performance metrics and constraints, and in each case show rates of convergence to the optimal (feasible) classifier (and thus asymptotic consistency). Experiments on a variety of multiclass classification tasks and fairness-constrained problems show that our algorithms compare favorably to the state-of-the-art baselines.