On the Effect of Image Resolution on Semantic Segmentation

High-resolution semantic segmentation requires substantial computational resources. Traditional approaches in the field typically downscale the input images before processing and then upscale the low-resolution outputs back to their original dimensions. While this strategy effectively identifies broad regions, it often misses finer details. In this study, we demonstrate that a streamlined model capable of directly producing high-resolution segmentations can match the performance of more complex systems that generate lower-resolution results. By simplifying the network architecture, we enable the processing of images at their native resolution. Our approach leverages a bottom-up information propagation technique across various scales, which we have empirically shown to enhance segmentation accuracy. We have rigorously tested our method using leading-edge semantic segmentation datasets. Specifically, for the Cityscapes dataset, we further boost accuracy by applying the Noisy Student Training technique.

Multiclass Learning from Noisy Labels for Non-decomposable Performance Measures

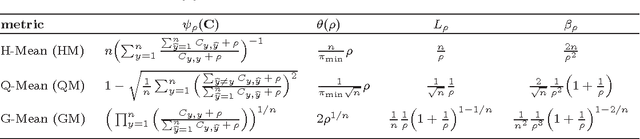
There has been much interest in recent years in learning good classifiers from data with noisy labels. Most work on learning from noisy labels has focused on standard loss-based performance measures. However, many machine learning problems require using non-decomposable performance measures which cannot be expressed as the expectation or sum of a loss on individual examples; these include for example the H-mean, Q-mean and G-mean in class imbalance settings, and the Micro $F_1$ in information retrieval. In this paper, we design algorithms to learn from noisy labels for two broad classes of multiclass non-decomposable performance measures, namely, monotonic convex and ratio-of-linear, which encompass all the above examples. Our work builds on the Frank-Wolfe and Bisection based methods of Narasimhan et al. (2015). In both cases, we develop noise-corrected versions of the algorithms under the widely studied family of class-conditional noise models. We provide regret (excess risk) bounds for our algorithms, establishing that even though they are trained on noisy data, they are Bayes consistent in the sense that their performance converges to the optimal performance w.r.t. the clean (non-noisy) distribution. Our experiments demonstrate the effectiveness of our algorithms in handling label noise.

MedSumm: A Multimodal Approach to Summarizing Code-Mixed Hindi-English Clinical Queries

In the healthcare domain, summarizing medical questions posed by patients is critical for improving doctor-patient interactions and medical decision-making. Although medical data has grown in complexity and quantity, the current body of research in this domain has primarily concentrated on text-based methods, overlooking the integration of visual cues. Also prior works in the area of medical question summarisation have been limited to the English language. This work introduces the task of multimodal medical question summarization for codemixed input in a low-resource setting. To address this gap, we introduce the Multimodal Medical Codemixed Question Summarization MMCQS dataset, which combines Hindi-English codemixed medical queries with visual aids. This integration enriches the representation of a patient's medical condition, providing a more comprehensive perspective. We also propose a framework named MedSumm that leverages the power of LLMs and VLMs for this task. By utilizing our MMCQS dataset, we demonstrate the value of integrating visual information from images to improve the creation of medically detailed summaries. This multimodal strategy not only improves healthcare decision-making but also promotes a deeper comprehension of patient queries, paving the way for future exploration in personalized and responsive medical care. Our dataset, code, and pre-trained models will be made publicly available.

Consistent Multiclass Algorithms for Complex Metrics and Constraints

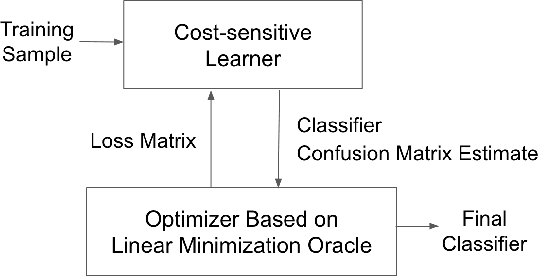
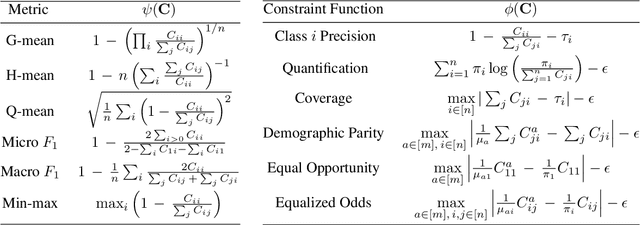
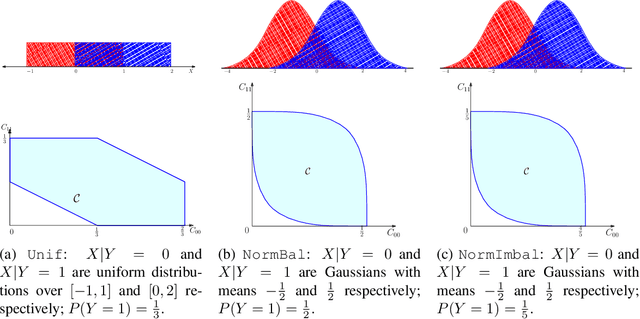
We present consistent algorithms for multiclass learning with complex performance metrics and constraints, where the objective and constraints are defined by arbitrary functions of the confusion matrix. This setting includes many common performance metrics such as the multiclass G-mean and micro F1-measure, and constraints such as those on the classifier's precision and recall and more recent measures of fairness discrepancy. We give a general framework for designing consistent algorithms for such complex design goals by viewing the learning problem as an optimization problem over the set of feasible confusion matrices. We provide multiple instantiations of our framework under different assumptions on the performance metrics and constraints, and in each case show rates of convergence to the optimal (feasible) classifier (and thus asymptotic consistency). Experiments on a variety of multiclass classification tasks and fairness-constrained problems show that our algorithms compare favorably to the state-of-the-art baselines.

Convex Calibrated Surrogates for the Multi-Label F-Measure

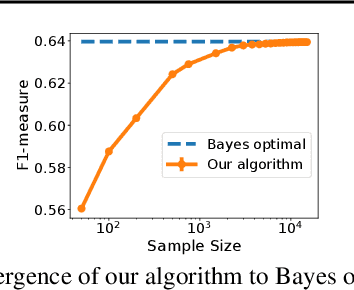
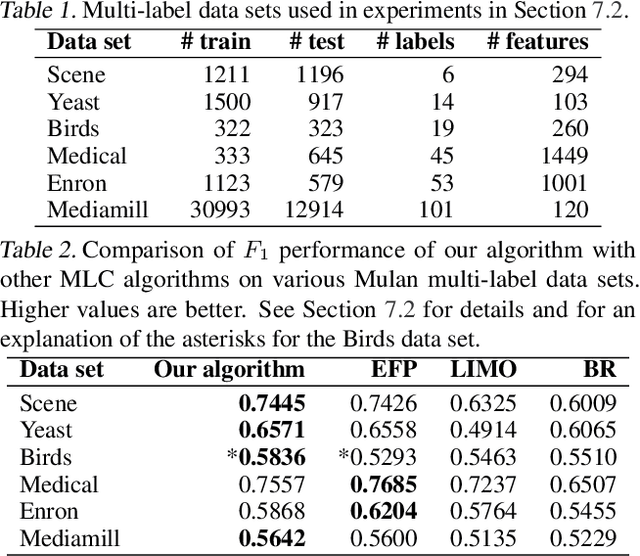
The F-measure is a widely used performance measure for multi-label classification, where multiple labels can be active in an instance simultaneously (e.g. in image tagging, multiple tags can be active in any image). In particular, the F-measure explicitly balances recall (fraction of active labels predicted to be active) and precision (fraction of labels predicted to be active that are actually so), both of which are important in evaluating the overall performance of a multi-label classifier. As with most discrete prediction problems, however, directly optimizing the F-measure is computationally hard. In this paper, we explore the question of designing convex surrogate losses that are calibrated for the F-measure -- specifically, that have the property that minimizing the surrogate loss yields (in the limit of sufficient data) a Bayes optimal multi-label classifier for the F-measure. We show that the F-measure for an $s$-label problem, when viewed as a $2^s \times 2^s$ loss matrix, has rank at most $s^2+1$, and apply a result of Ramaswamy et al. (2014) to design a family of convex calibrated surrogates for the F-measure. The resulting surrogate risk minimization algorithms can be viewed as decomposing the multi-label F-measure learning problem into $s^2+1$ binary class probability estimation problems. We also provide a quantitative regret transfer bound for our surrogates, which allows any regret guarantees for the binary problems to be transferred to regret guarantees for the overall F-measure problem, and discuss a connection with the algorithm of Dembczynski et al. (2013). Our experiments confirm our theoretical findings.

Support Vector Algorithms for Optimizing the Partial Area Under the ROC Curve

The area under the ROC curve (AUC) is a widely used performance measure in machine learning. Increasingly, however, in several applications, ranging from ranking to biometric screening to medicine, performance is measured not in terms of the full area under the ROC curve, but in terms of the \emph{partial} area under the ROC curve between two false positive rates. In this paper, we develop support vector algorithms for directly optimizing the partial AUC between any two false positive rates. Our methods are based on minimizing a suitable proxy or surrogate objective for the partial AUC error. In the case of the full AUC, one can readily construct and optimize convex surrogates by expressing the performance measure as a summation of pairwise terms. The partial AUC, on the other hand, does not admit such a simple decomposable structure, making it more challenging to design and optimize (tight) convex surrogates for this measure. Our approach builds on the structural SVM framework of Joachims (2005) to design convex surrogates for partial AUC, and solves the resulting optimization problem using a cutting plane solver. Unlike the full AUC, where the combinatorial optimization needed in each iteration of the cutting plane solver can be decomposed and solved efficiently, the corresponding problem for the partial AUC is harder to decompose. One of our main contributions is a polynomial time algorithm for solving the combinatorial optimization problem associated with partial AUC. We also develop an approach for optimizing a tighter non-convex hinge loss based surrogate for the partial AUC using difference-of-convex programming. Our experiments on a variety of real-world and benchmark tasks confirm the efficacy of the proposed methods.

Convex Calibration Dimension for Multiclass Loss Matrices

We study consistency properties of surrogate loss functions for general multiclass learning problems, defined by a general multiclass loss matrix. We extend the notion of classification calibration, which has been studied for binary and multiclass 0-1 classification problems (and for certain other specific learning problems), to the general multiclass setting, and derive necessary and sufficient conditions for a surrogate loss to be calibrated with respect to a loss matrix in this setting. We then introduce the notion of convex calibration dimension of a multiclass loss matrix, which measures the smallest `size' of a prediction space in which it is possible to design a convex surrogate that is calibrated with respect to the loss matrix. We derive both upper and lower bounds on this quantity, and use these results to analyze various loss matrices. In particular, we apply our framework to study various subset ranking losses, and use the convex calibration dimension as a tool to show both the existence and non-existence of various types of convex calibrated surrogates for these losses. Our results strengthen recent results of Duchi et al. (2010) and Calauzenes et al. (2012) on the non-existence of certain types of convex calibrated surrogates in subset ranking. We anticipate the convex calibration dimension may prove to be a useful tool in the study and design of surrogate losses for general multiclass learning problems.

Consistent Algorithms for Multiclass Classification with a Reject Option

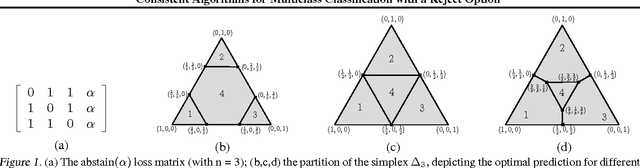
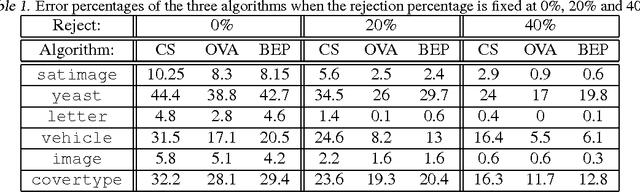
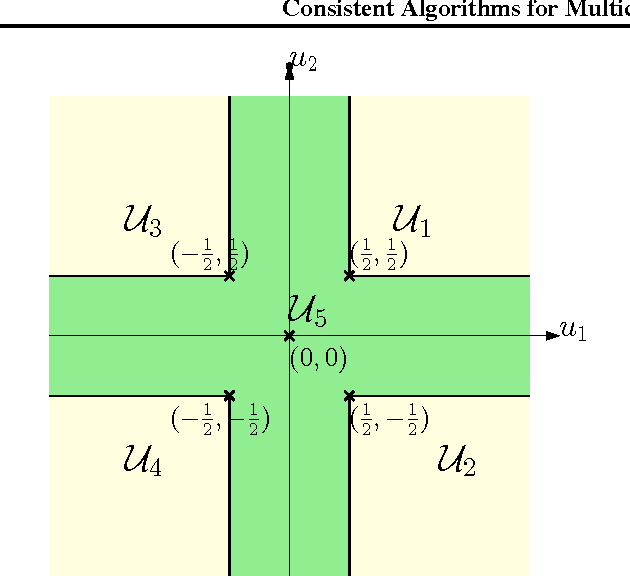
We consider the problem of $n$-class classification ($n\geq 2$), where the classifier can choose to abstain from making predictions at a given cost, say, a factor $\alpha$ of the cost of misclassification. Designing consistent algorithms for such $n$-class classification problems with a `reject option' is the main goal of this paper, thereby extending and generalizing previously known results for $n=2$. We show that the Crammer-Singer surrogate and the one vs all hinge loss, albeit with a different predictor than the standard argmax, yield consistent algorithms for this problem when $\alpha=\frac{1}{2}$. More interestingly, we design a new convex surrogate that is also consistent for this problem when $\alpha=\frac{1}{2}$ and operates on a much lower dimensional space ($\log(n)$ as opposed to $n$). We also generalize all three surrogates to be consistent for any $\alpha\in[0, \frac{1}{2}]$.

Consistent Classification Algorithms for Multi-class Non-Decomposable Performance Metrics

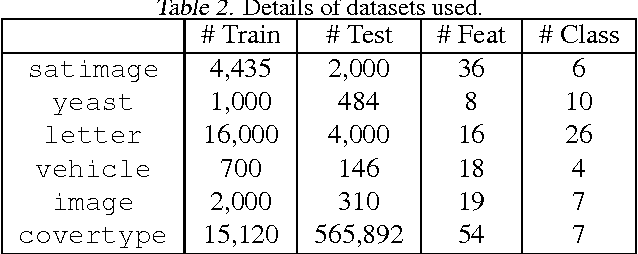
We study consistency of learning algorithms for a multi-class performance metric that is a non-decomposable function of the confusion matrix of a classifier and cannot be expressed as a sum of losses on individual data points; examples of such performance metrics include the macro F-measure popular in information retrieval and the G-mean metric used in class-imbalanced problems. While there has been much work in recent years in understanding the consistency properties of learning algorithms for `binary' non-decomposable metrics, little is known either about the form of the optimal classifier for a general multi-class non-decomposable metric, or about how these learning algorithms generalize to the multi-class case. In this paper, we provide a unified framework for analysing a multi-class non-decomposable performance metric, where the problem of finding the optimal classifier for the performance metric is viewed as an optimization problem over the space of all confusion matrices achievable under the given distribution. Using this framework, we show that (under a continuous distribution) the optimal classifier for a multi-class performance metric can be obtained as the solution of a cost-sensitive classification problem, thus generalizing several previous results on specific binary non-decomposable metrics. We then design a consistent learning algorithm for concave multi-class performance metrics that proceeds via a sequence of cost-sensitive classification problems, and can be seen as applying the conditional gradient (CG) optimization method over the space of feasible confusion matrices. To our knowledge, this is the first efficient learning algorithm (whose running time is polynomial in the number of classes) that is consistent for a large family of multi-class non-decomposable metrics. Our consistency proof uses a novel technique based on the convergence analysis of the CG method.

Surrogate Regret Bounds for Bipartite Ranking via Strongly Proper Losses

The problem of bipartite ranking, where instances are labeled positive or negative and the goal is to learn a scoring function that minimizes the probability of mis-ranking a pair of positive and negative instances (or equivalently, that maximizes the area under the ROC curve), has been widely studied in recent years. A dominant theoretical and algorithmic framework for the problem has been to reduce bipartite ranking to pairwise classification; in particular, it is well known that the bipartite ranking regret can be formulated as a pairwise classification regret, which in turn can be upper bounded using usual regret bounds for classification problems. Recently, Kotlowski et al. (2011) showed regret bounds for bipartite ranking in terms of the regret associated with balanced versions of the standard (non-pairwise) logistic and exponential losses. In this paper, we show that such (non-pairwise) surrogate regret bounds for bipartite ranking can be obtained in terms of a broad class of proper (composite) losses that we term as strongly proper. Our proof technique is much simpler than that of Kotlowski et al. (2011), and relies on properties of proper (composite) losses as elucidated recently by Reid and Williamson (2010, 2011) and others. Our result yields explicit surrogate bounds (with no hidden balancing terms) in terms of a variety of strongly proper losses, including for example logistic, exponential, squared and squared hinge losses as special cases. We also obtain tighter surrogate bounds under certain low-noise conditions via a recent result of Clemencon and Robbiano (2011).