Consistent Algorithms for Multiclass Classification with a Reject Option
Paper and Code
May 15, 2015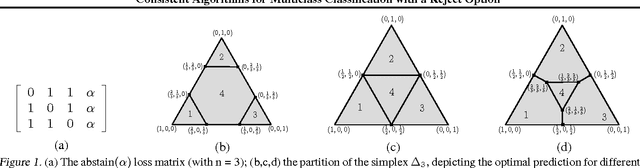
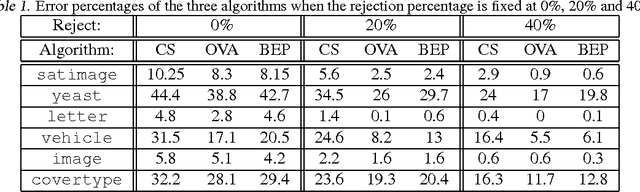
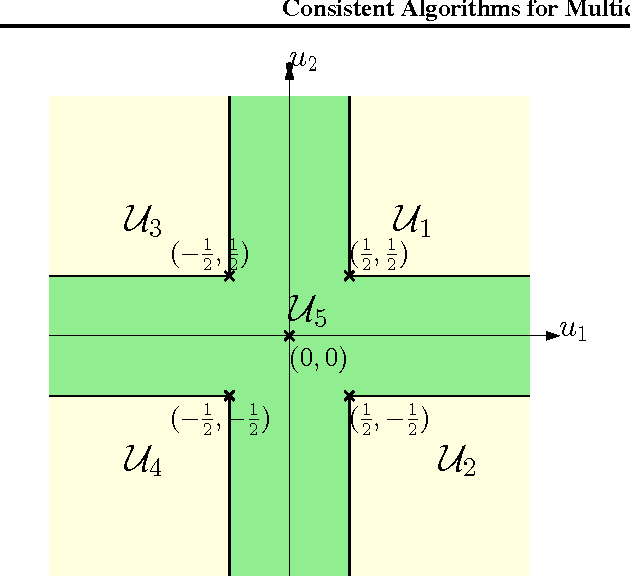
We consider the problem of $n$-class classification ($n\geq 2$), where the classifier can choose to abstain from making predictions at a given cost, say, a factor $\alpha$ of the cost of misclassification. Designing consistent algorithms for such $n$-class classification problems with a `reject option' is the main goal of this paper, thereby extending and generalizing previously known results for $n=2$. We show that the Crammer-Singer surrogate and the one vs all hinge loss, albeit with a different predictor than the standard argmax, yield consistent algorithms for this problem when $\alpha=\frac{1}{2}$. More interestingly, we design a new convex surrogate that is also consistent for this problem when $\alpha=\frac{1}{2}$ and operates on a much lower dimensional space ($\log(n)$ as opposed to $n$). We also generalize all three surrogates to be consistent for any $\alpha\in[0, \frac{1}{2}]$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge