Universal Model Routing for Efficient LLM Inference

Large language models' significant advances in capabilities are accompanied by significant increases in inference costs. Model routing is a simple technique for reducing inference cost, wherein one maintains a pool of candidate LLMs, and learns to route each prompt to the smallest feasible LLM. Existing works focus on learning a router for a fixed pool of LLMs. In this paper, we consider the problem of dynamic routing, where new, previously unobserved LLMs are available at test time. We propose a new approach to this problem that relies on representing each LLM as a feature vector, derived based on predictions on a set of representative prompts. Based on this, we detail two effective strategies, relying on cluster-based routing and a learned cluster map respectively. We prove that these strategies are estimates of a theoretically optimal routing rule, and provide an excess risk bound to quantify their errors. Experiments on a range of public benchmarks show the effectiveness of the proposed strategies in routing amongst more than 30 unseen LLMs.

StagFormer: Time Staggering Transformer Decoding for RunningLayers In Parallel

Standard decoding in a Transformer based language model is inherently sequential as we wait for a token's embedding to pass through all the layers in the network before starting the generation of the next token. In this work, we propose a new architecture StagFormer (Staggered Transformer), which staggered execution along the time axis and thereby enables parallelizing the decoding process along the depth of the model. We achieve this by breaking the dependency of the token representation at time step $i$ in layer $l$ upon the representations of tokens until time step $i$ from layer $l-1$. Instead, we stagger the execution and only allow a dependency on token representations until time step $i-1$. The later sections of the Transformer still get access to the ``rich" representations from the prior section but only from those token positions which are one time step behind. StagFormer allows for different sections of the model to be executed in parallel yielding at potential 33\% speedup in decoding while being quality neutral in our simulations. We also explore many natural variants of this idea. We present how weight-sharing across the different sections being staggered can be more practical in settings with limited memory. We show how one can approximate a recurrent model during inference using such weight-sharing. We explore the efficacy of using a bounded window attention to pass information from one section to another which helps drive further latency gains for some applications. We also explore demonstrate the scalability of the staggering idea over more than 2 sections of the Transformer.

How Transformers Solve Propositional Logic Problems: A Mechanistic Analysis

Large language models (LLMs) have shown amazing performance on tasks that require planning and reasoning. Motivated by this, we investigate the internal mechanisms that underpin a network's ability to perform complex logical reasoning. We first construct a synthetic propositional logic problem that serves as a concrete test-bed for network training and evaluation. Crucially, this problem demands nontrivial planning to solve, but we can train a small transformer to achieve perfect accuracy. Building on our set-up, we then pursue an understanding of precisely how a three-layer transformer, trained from scratch, solves this problem. We are able to identify certain "planning" and "reasoning" circuits in the network that necessitate cooperation between the attention blocks to implement the desired logic. To expand our findings, we then study a larger model, Mistral 7B. Using activation patching, we characterize internal components that are critical in solving our logic problem. Overall, our work systemically uncovers novel aspects of small and large transformers, and continues the study of how they plan and reason.

Causal Language Modeling Can Elicit Search and Reasoning Capabilities on Logic Puzzles

Causal language modeling using the Transformer architecture has yielded remarkable capabilities in Large Language Models (LLMs) over the last few years. However, the extent to which fundamental search and reasoning capabilities emerged within LLMs remains a topic of ongoing debate. In this work, we study if causal language modeling can learn a complex task such as solving Sudoku puzzles. To solve a Sudoku, the model is first required to search over all empty cells of the puzzle to decide on a cell to fill and then apply an appropriate strategy to fill the decided cell. Sometimes, the application of a strategy only results in thinning down the possible values in a cell rather than concluding the exact value of the cell. In such cases, multiple strategies are applied one after the other to fill a single cell. We observe that Transformer models trained on this synthetic task can indeed learn to solve Sudokus (our model solves $94.21\%$ of the puzzles fully correctly) when trained on a logical sequence of steps taken by a solver. We find that training Transformers with the logical sequence of steps is necessary and without such training, they fail to learn Sudoku. We also extend our analysis to Zebra puzzles (known as Einstein puzzles) and show that the model solves $92.04 \%$ of the puzzles fully correctly. In addition, we study the internal representations of the trained Transformer and find that through linear probing, we can decode information about the set of possible values in any given cell from them, pointing to the presence of a strong reasoning engine implicit in the Transformer weights.

Simple Mechanisms for Representing, Indexing and Manipulating Concepts

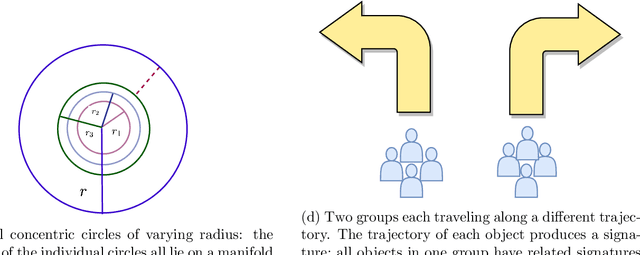
Deep networks typically learn concepts via classifiers, which involves setting up a model and training it via gradient descent to fit the concept-labeled data. We will argue instead that learning a concept could be done by looking at its moment statistics matrix to generate a concrete representation or signature of that concept. These signatures can be used to discover structure across the set of concepts and could recursively produce higher-level concepts by learning this structure from those signatures. When the concepts are `intersected', signatures of the concepts can be used to find a common theme across a number of related `intersected' concepts. This process could be used to keep a dictionary of concepts so that inputs could correctly identify and be routed to the set of concepts involved in the (latent) generation of the input.

The Power of External Memory in Increasing Predictive Model Capacity

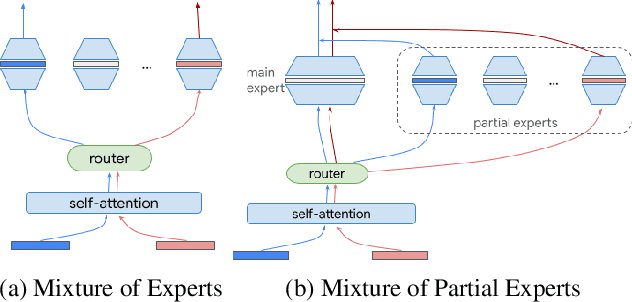
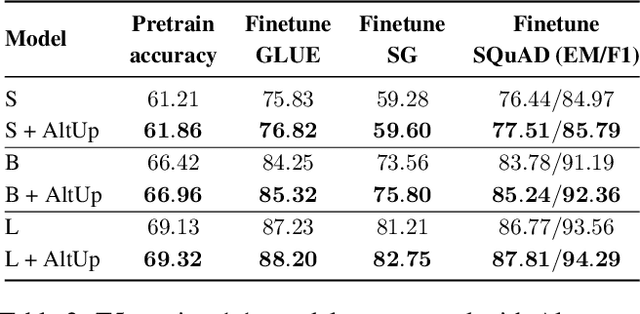
One way of introducing sparsity into deep networks is by attaching an external table of parameters that is sparsely looked up at different layers of the network. By storing the bulk of the parameters in the external table, one can increase the capacity of the model without necessarily increasing the inference time. Two crucial questions in this setting are then: what is the lookup function for accessing the table and how are the contents of the table consumed? Prominent methods for accessing the table include 1) using words/wordpieces token-ids as table indices, 2) LSH hashing the token vector in each layer into a table of buckets, and 3) learnable softmax style routing to a table entry. The ways to consume the contents include adding/concatenating to input representation, and using the contents as expert networks that specialize to different inputs. In this work, we conduct rigorous experimental evaluations of existing ideas and their combinations. We also introduce a new method, alternating updates, that enables access to an increased token dimension without increasing the computation time, and demonstrate its effectiveness in language modeling.

Alternating Updates for Efficient Transformers

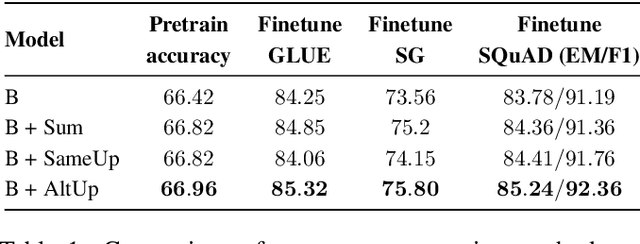
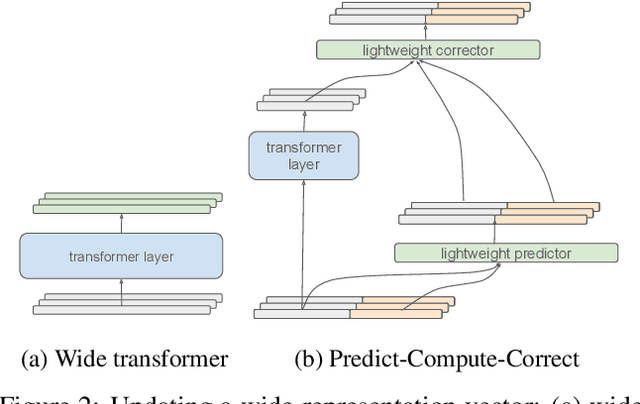
It is well established that increasing scale in deep transformer networks leads to improved quality and performance. This increase in scale often comes with an increase in compute cost and inference latency. Consequently, research into methods which help realize the benefits of increased scale without leading to an increase in the compute cost becomes important. We introduce Alternating Updates (AltUp), a simple-to-implement method to increase a model's capacity without the computational burden. AltUp enables the widening of the learned representation without increasing the computation time by working on a subblock of the representation at each layer. Our experiments on various transformer models and language tasks demonstrate the consistent effectiveness of alternating updates on a diverse set of benchmarks. Finally, we present extensions of AltUp to the sequence dimension, and demonstrate how AltUp can be synergistically combined with existing approaches, such as Sparse Mixture-of-Experts models, to obtain efficient models with even higher capacity.

A Theoretical View on Sparsely Activated Networks

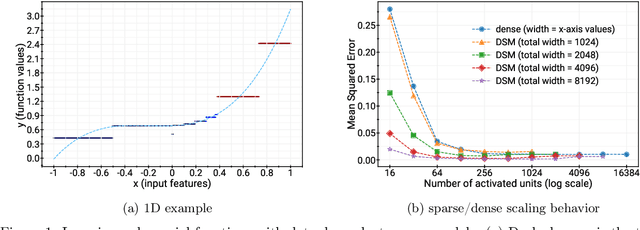
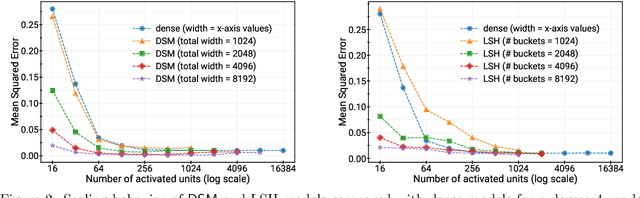
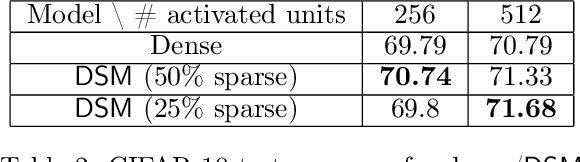
Deep and wide neural networks successfully fit very complex functions today, but dense models are starting to be prohibitively expensive for inference. To mitigate this, one promising direction is networks that activate a sparse subgraph of the network. The subgraph is chosen by a data-dependent routing function, enforcing a fixed mapping of inputs to subnetworks (e.g., the Mixture of Experts (MoE) paradigm in Switch Transformers). However, prior work is largely empirical, and while existing routing functions work well in practice, they do not lead to theoretical guarantees on approximation ability. We aim to provide a theoretical explanation for the power of sparse networks. As our first contribution, we present a formal model of data-dependent sparse networks that captures salient aspects of popular architectures. We then introduce a routing function based on locality sensitive hashing (LSH) that enables us to reason about how well sparse networks approximate target functions. After representing LSH-based sparse networks with our model, we prove that sparse networks can match the approximation power of dense networks on Lipschitz functions. Applying LSH on the input vectors means that the experts interpolate the target function in different subregions of the input space. To support our theory, we define various datasets based on Lipschitz target functions, and we show that sparse networks give a favorable trade-off between number of active units and approximation quality.

A Unified Cascaded Encoder ASR Model for Dynamic Model Sizes

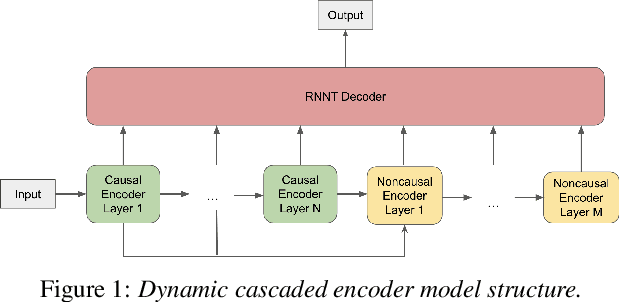
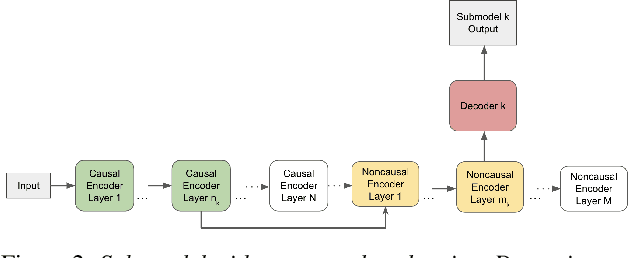
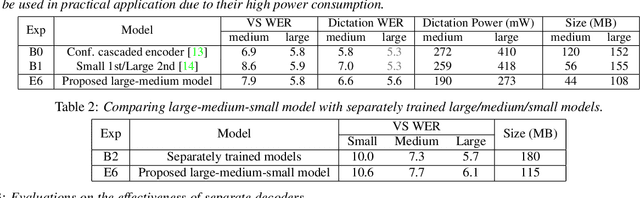
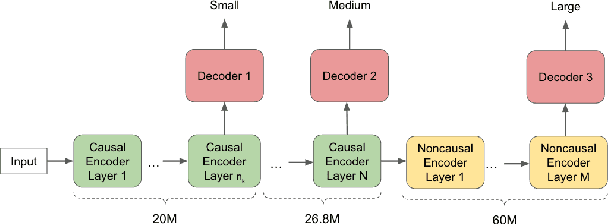
In this paper, we propose a dynamic cascaded encoder Automatic Speech Recognition (ASR) model, which unifies models for different deployment scenarios. Moreover, the model can significantly reduce model size and power consumption without loss of quality. Namely, with the dynamic cascaded encoder model, we explore three techniques to maximally boost the performance of each model size: 1) Use separate decoders for each sub-model while sharing the encoders; 2) Use funnel-pooling to improve the encoder efficiency; 3) Balance the size of causal and non-causal encoders to improve quality and fit deployment constraints. Overall, the proposed large-medium model has 30% smaller size and reduces power consumption by 33%, compared to the baseline cascaded encoder model. The triple-size model that unifies the large, medium, and small models achieves 37% total size reduction with minimal quality loss, while substantially reducing the engineering efforts of having separate models.

Provable Hierarchical Lifelong Learning with a Sketch-based Modular Architecture

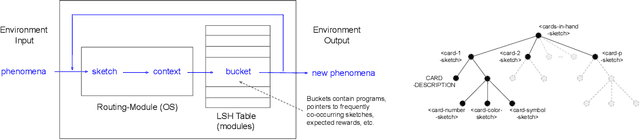
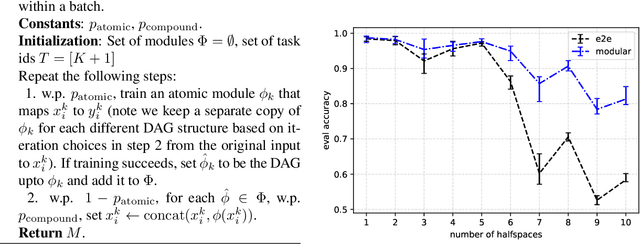
We propose a modular architecture for the lifelong learning of hierarchically structured tasks. Specifically, we prove that our architecture is theoretically able to learn tasks that can be solved by functions that are learnable given access to functions for other, previously learned tasks as subroutines. We empirically show that some tasks that we can learn in this way are not learned by standard training methods in practice; indeed, prior work suggests that some such tasks cannot be learned by any efficient method without the aid of the simpler tasks. We also consider methods for identifying the tasks automatically, without relying on explicitly given indicators.