BIG-Bench Extra Hard

Large language models (LLMs) are increasingly deployed in everyday applications, demanding robust general reasoning capabilities and diverse reasoning skillset. However, current LLM reasoning benchmarks predominantly focus on mathematical and coding abilities, leaving a gap in evaluating broader reasoning proficiencies. One particular exception is the BIG-Bench dataset, which has served as a crucial benchmark for evaluating the general reasoning capabilities of LLMs, thanks to its diverse set of challenging tasks that allowed for a comprehensive assessment of general reasoning across various skills within a unified framework. However, recent advances in LLMs have led to saturation on BIG-Bench, and its harder version BIG-Bench Hard (BBH). State-of-the-art models achieve near-perfect scores on many tasks in BBH, thus diminishing its utility. To address this limitation, we introduce BIG-Bench Extra Hard (BBEH), a new benchmark designed to push the boundaries of LLM reasoning evaluation. BBEH replaces each task in BBH with a novel task that probes a similar reasoning capability but exhibits significantly increased difficulty. We evaluate various models on BBEH and observe a (harmonic) average accuracy of 9.8\% for the best general-purpose model and 44.8\% for the best reasoning-specialized model, indicating substantial room for improvement and highlighting the ongoing challenge of achieving robust general reasoning in LLMs. We release BBEH publicly at: https://github.com/google-deepmind/bbeh.

Reasoning with Latent Thoughts: On the Power of Looped Transformers

Large language models have shown remarkable reasoning abilities and scaling laws suggest that large parameter count, especially along the depth axis, is the primary driver. In this work, we make a stronger claim -- many reasoning problems require a large depth but not necessarily many parameters. This unlocks a novel application of looped models for reasoning. Firstly, we show that for many synthetic reasoning problems like addition, $p$-hop induction, and math problems, a $k$-layer transformer looped $L$ times nearly matches the performance of a $kL$-layer non-looped model, and is significantly better than a $k$-layer model. This is further corroborated by theoretical results showing that many such reasoning problems can be solved via iterative algorithms, and thus, can be solved effectively using looped models with nearly optimal depth. Perhaps surprisingly, these benefits also translate to practical settings of language modeling -- on many downstream reasoning tasks, a language model with $k$-layers looped $L$ times can be competitive to, if not better than, a $kL$-layer language model. In fact, our empirical analysis reveals an intriguing phenomenon: looped and non-looped models exhibit scaling behavior that depends on their effective depth, akin to the inference-time scaling of chain-of-thought (CoT) reasoning. We further elucidate the connection to CoT reasoning by proving that looped models implicitly generate latent thoughts and can simulate $T$ steps of CoT with $T$ loops. Inspired by these findings, we also present an interesting dichotomy between reasoning and memorization, and design a looping-based regularization that is effective on both fronts.

StagFormer: Time Staggering Transformer Decoding for RunningLayers In Parallel

Standard decoding in a Transformer based language model is inherently sequential as we wait for a token's embedding to pass through all the layers in the network before starting the generation of the next token. In this work, we propose a new architecture StagFormer (Staggered Transformer), which staggered execution along the time axis and thereby enables parallelizing the decoding process along the depth of the model. We achieve this by breaking the dependency of the token representation at time step $i$ in layer $l$ upon the representations of tokens until time step $i$ from layer $l-1$. Instead, we stagger the execution and only allow a dependency on token representations until time step $i-1$. The later sections of the Transformer still get access to the ``rich" representations from the prior section but only from those token positions which are one time step behind. StagFormer allows for different sections of the model to be executed in parallel yielding at potential 33\% speedup in decoding while being quality neutral in our simulations. We also explore many natural variants of this idea. We present how weight-sharing across the different sections being staggered can be more practical in settings with limited memory. We show how one can approximate a recurrent model during inference using such weight-sharing. We explore the efficacy of using a bounded window attention to pass information from one section to another which helps drive further latency gains for some applications. We also explore demonstrate the scalability of the staggering idea over more than 2 sections of the Transformer.

How Transformers Solve Propositional Logic Problems: A Mechanistic Analysis

Large language models (LLMs) have shown amazing performance on tasks that require planning and reasoning. Motivated by this, we investigate the internal mechanisms that underpin a network's ability to perform complex logical reasoning. We first construct a synthetic propositional logic problem that serves as a concrete test-bed for network training and evaluation. Crucially, this problem demands nontrivial planning to solve, but we can train a small transformer to achieve perfect accuracy. Building on our set-up, we then pursue an understanding of precisely how a three-layer transformer, trained from scratch, solves this problem. We are able to identify certain "planning" and "reasoning" circuits in the network that necessitate cooperation between the attention blocks to implement the desired logic. To expand our findings, we then study a larger model, Mistral 7B. Using activation patching, we characterize internal components that are critical in solving our logic problem. Overall, our work systemically uncovers novel aspects of small and large transformers, and continues the study of how they plan and reason.

Causal Language Modeling Can Elicit Search and Reasoning Capabilities on Logic Puzzles

Causal language modeling using the Transformer architecture has yielded remarkable capabilities in Large Language Models (LLMs) over the last few years. However, the extent to which fundamental search and reasoning capabilities emerged within LLMs remains a topic of ongoing debate. In this work, we study if causal language modeling can learn a complex task such as solving Sudoku puzzles. To solve a Sudoku, the model is first required to search over all empty cells of the puzzle to decide on a cell to fill and then apply an appropriate strategy to fill the decided cell. Sometimes, the application of a strategy only results in thinning down the possible values in a cell rather than concluding the exact value of the cell. In such cases, multiple strategies are applied one after the other to fill a single cell. We observe that Transformer models trained on this synthetic task can indeed learn to solve Sudokus (our model solves $94.21\%$ of the puzzles fully correctly) when trained on a logical sequence of steps taken by a solver. We find that training Transformers with the logical sequence of steps is necessary and without such training, they fail to learn Sudoku. We also extend our analysis to Zebra puzzles (known as Einstein puzzles) and show that the model solves $92.04 \%$ of the puzzles fully correctly. In addition, we study the internal representations of the trained Transformer and find that through linear probing, we can decode information about the set of possible values in any given cell from them, pointing to the presence of a strong reasoning engine implicit in the Transformer weights.

Learning Neural Networks with Sparse Activations

A core component present in many successful neural network architectures, is an MLP block of two fully connected layers with a non-linear activation in between. An intriguing phenomenon observed empirically, including in transformer architectures, is that, after training, the activations in the hidden layer of this MLP block tend to be extremely sparse on any given input. Unlike traditional forms of sparsity, where there are neurons/weights which can be deleted from the network, this form of {\em dynamic} activation sparsity appears to be harder to exploit to get more efficient networks. Motivated by this we initiate a formal study of PAC learnability of MLP layers that exhibit activation sparsity. We present a variety of results showing that such classes of functions do lead to provable computational and statistical advantages over their non-sparse counterparts. Our hope is that a better theoretical understanding of {\em sparsely activated} networks would lead to methods that can exploit activation sparsity in practice.

ReMI: A Dataset for Reasoning with Multiple Images

With the continuous advancement of large language models (LLMs), it is essential to create new benchmarks to effectively evaluate their expanding capabilities and identify areas for improvement. This work focuses on multi-image reasoning, an emerging capability in state-of-the-art LLMs. We introduce ReMI, a dataset designed to assess LLMs' ability to Reason with Multiple Images. This dataset encompasses a diverse range of tasks, spanning various reasoning domains such as math, physics, logic, code, table/chart understanding, and spatial and temporal reasoning. It also covers a broad spectrum of characteristics found in multi-image reasoning scenarios. We have benchmarked several cutting-edge LLMs using ReMI and found a substantial gap between their performance and human-level proficiency. This highlights the challenges in multi-image reasoning and the need for further research. Our analysis also reveals the strengths and weaknesses of different models, shedding light on the types of reasoning that are currently attainable and areas where future models require improvement. To foster further research in this area, we are releasing ReMI publicly: https://huggingface.co/datasets/mehrankazemi/ReMI.

The Power of External Memory in Increasing Predictive Model Capacity

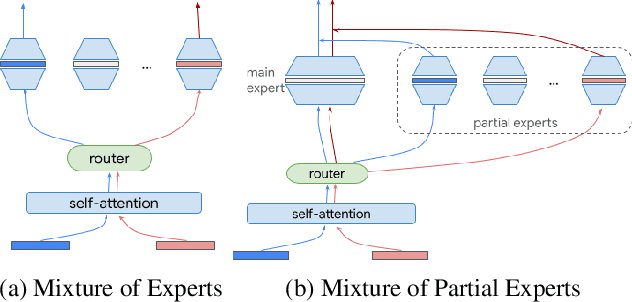
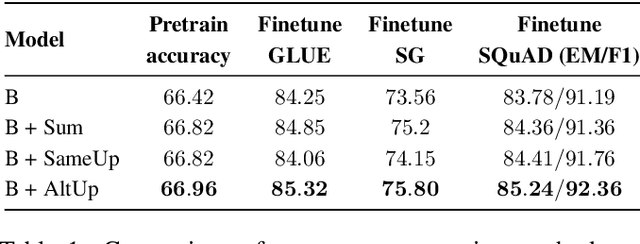
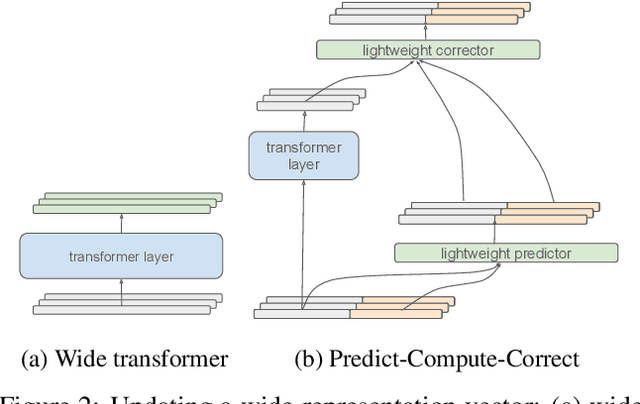
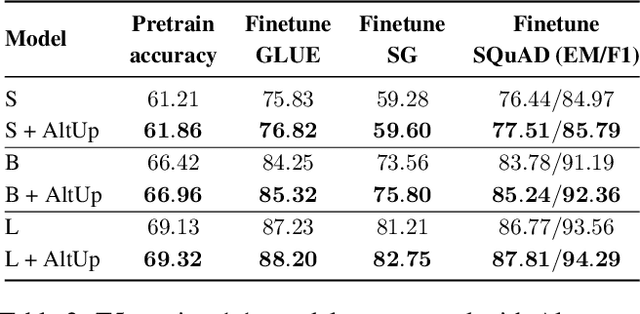
One way of introducing sparsity into deep networks is by attaching an external table of parameters that is sparsely looked up at different layers of the network. By storing the bulk of the parameters in the external table, one can increase the capacity of the model without necessarily increasing the inference time. Two crucial questions in this setting are then: what is the lookup function for accessing the table and how are the contents of the table consumed? Prominent methods for accessing the table include 1) using words/wordpieces token-ids as table indices, 2) LSH hashing the token vector in each layer into a table of buckets, and 3) learnable softmax style routing to a table entry. The ways to consume the contents include adding/concatenating to input representation, and using the contents as expert networks that specialize to different inputs. In this work, we conduct rigorous experimental evaluations of existing ideas and their combinations. We also introduce a new method, alternating updates, that enables access to an increased token dimension without increasing the computation time, and demonstrate its effectiveness in language modeling.

Alternating Updates for Efficient Transformers

It is well established that increasing scale in deep transformer networks leads to improved quality and performance. This increase in scale often comes with an increase in compute cost and inference latency. Consequently, research into methods which help realize the benefits of increased scale without leading to an increase in the compute cost becomes important. We introduce Alternating Updates (AltUp), a simple-to-implement method to increase a model's capacity without the computational burden. AltUp enables the widening of the learned representation without increasing the computation time by working on a subblock of the representation at each layer. Our experiments on various transformer models and language tasks demonstrate the consistent effectiveness of alternating updates on a diverse set of benchmarks. Finally, we present extensions of AltUp to the sequence dimension, and demonstrate how AltUp can be synergistically combined with existing approaches, such as Sparse Mixture-of-Experts models, to obtain efficient models with even higher capacity.

A Theoretical View on Sparsely Activated Networks

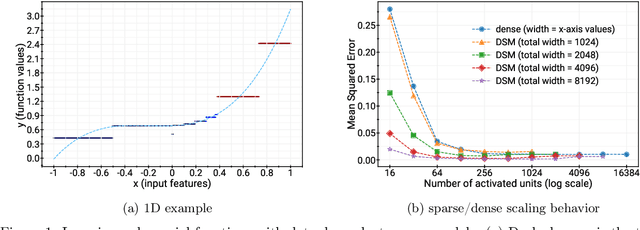
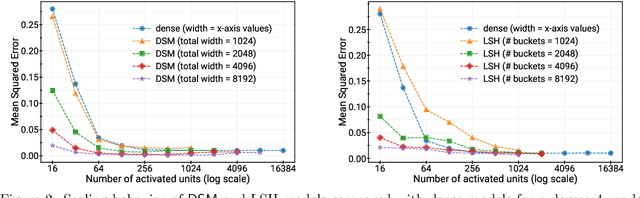
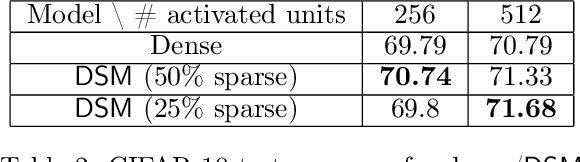
Deep and wide neural networks successfully fit very complex functions today, but dense models are starting to be prohibitively expensive for inference. To mitigate this, one promising direction is networks that activate a sparse subgraph of the network. The subgraph is chosen by a data-dependent routing function, enforcing a fixed mapping of inputs to subnetworks (e.g., the Mixture of Experts (MoE) paradigm in Switch Transformers). However, prior work is largely empirical, and while existing routing functions work well in practice, they do not lead to theoretical guarantees on approximation ability. We aim to provide a theoretical explanation for the power of sparse networks. As our first contribution, we present a formal model of data-dependent sparse networks that captures salient aspects of popular architectures. We then introduce a routing function based on locality sensitive hashing (LSH) that enables us to reason about how well sparse networks approximate target functions. After representing LSH-based sparse networks with our model, we prove that sparse networks can match the approximation power of dense networks on Lipschitz functions. Applying LSH on the input vectors means that the experts interpolate the target function in different subregions of the input space. To support our theory, we define various datasets based on Lipschitz target functions, and we show that sparse networks give a favorable trade-off between number of active units and approximation quality.