Control, Transport and Sampling: Towards Better Loss Design

Leveraging connections between diffusion-based sampling, optimal transport, and optimal stochastic control through their shared links to the Schr\"odinger bridge problem, we propose novel objective functions that can be used to transport $\nu$ to $\mu$, consequently sample from the target $\mu$, via optimally controlled dynamics. We highlight the importance of the pathwise perspective and the role various optimality conditions on the path measure can play for the design of valid training losses, the careful choice of which offer numerical advantages in practical implementation.

From Estimation to Sampling for Bayesian Linear Regression with Spike-and-Slab Prior

We consider Bayesian linear regression with sparsity-inducing prior and design efficient sampling algorithms leveraging posterior contraction properties. A quasi-likelihood with Gaussian spike-and-slab (that is favorable both statistically and computationally) is investigated and two algorithms based on Gibbs sampling and Stochastic Localization are analyzed, both under the same (quite natural) statistical assumptions that also enable valid inference on the sparse planted signal. The benefit of the Stochastic Localization sampler is particularly prominent for data matrix that is not well-designed.

On the Dissipation of Ideal Hamiltonian Monte Carlo Sampler

We report on what seems to be an intriguing connection between variable integration time and partial velocity refreshment of Ideal Hamiltonian Monte Carlo samplers, both of which can be used for reducing the dissipative behavior of the dynamics. More concretely, we show that on quadratic potentials, efficiency can be improved through these means by a $\sqrt{\kappa}$ factor in Wasserstein-2 distance, compared to classical constant integration time, fully refreshed HMC.

Learning the Truth From Only One Side of the Story

Learning under one-sided feedback (i.e., where examples arrive in an online fashion and the learner only sees the labels for examples it predicted positively on) is a fundamental problem in machine learning -- applications include lending and recommendation systems. Despite this, there has been surprisingly little progress made in ways to mitigate the effects of the sampling bias that arises. We focus on generalized linear models and show that without adjusting for this sampling bias, the model may converge sub-optimally or even fail to converge to the optimal solution. We propose an adaptive Upper Confidence Bound approach that comes with rigorous regret guarantees and we show that it outperforms several existing methods experimentally. Our method leverages uncertainty estimation techniques for generalized linear models to more efficiently explore uncertain areas than existing approaches which explore randomly.

Optimizing Black-box Metrics with Adaptive Surrogates

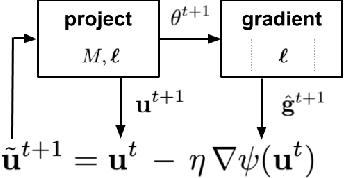
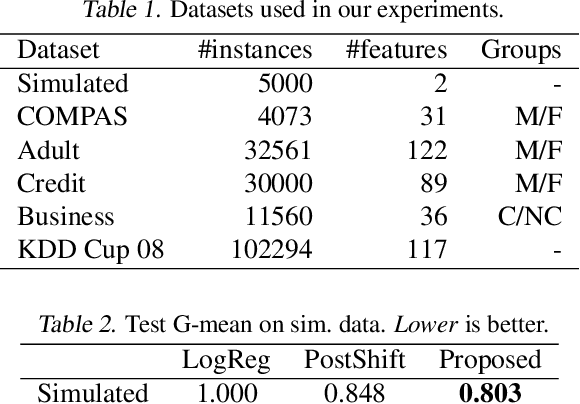
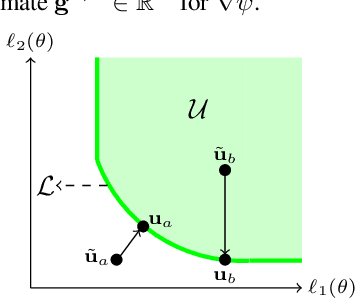
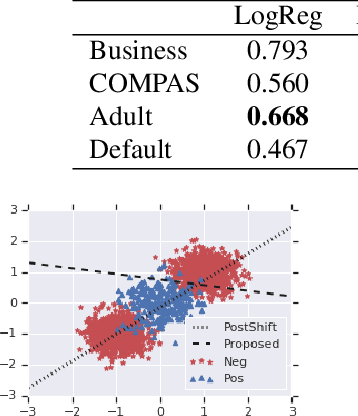
We address the problem of training models with black-box and hard-to-optimize metrics by expressing the metric as a monotonic function of a small number of easy-to-optimize surrogates. We pose the training problem as an optimization over a relaxed surrogate space, which we solve by estimating local gradients for the metric and performing inexact convex projections. We analyze gradient estimates based on finite differences and local linear interpolations, and show convergence of our approach under smoothness assumptions with respect to the surrogates. Experimental results on classification and ranking problems verify the proposal performs on par with methods that know the mathematical formulation, and adds notable value when the form of the metric is unknown.

Complexity of Highly Parallel Non-Smooth Convex Optimization

A landmark result of non-smooth convex optimization is that gradient descent is an optimal algorithm whenever the number of computed gradients is smaller than the dimension $d$. In this paper we study the extension of this result to the parallel optimization setting. Namely we consider optimization algorithms interacting with a highly parallel gradient oracle, that is one that can answer $\mathrm{poly}(d)$ gradient queries in parallel. We show that in this case gradient descent is optimal only up to $\tilde{O}(\sqrt{d})$ rounds of interactions with the oracle. The lower bound improves upon a decades old construction by Nemirovski which proves optimality only up to $d^{1/3}$ rounds (as recently observed by Balkanski and Singer), and the suboptimality of gradient descent after $\sqrt{d}$ rounds was already observed by Duchi, Bartlett and Wainwright. In the latter regime we propose a new method with improved complexity, which we conjecture to be optimal. The analysis of this new method is based upon a generalized version of the recent results on optimal acceleration for highly smooth convex optimization.

Subgradient Descent Learns Orthogonal Dictionaries

This paper concerns dictionary learning, i.e., sparse coding, a fundamental representation learning problem. We show that a subgradient descent algorithm, with random initialization, can provably recover orthogonal dictionaries on a natural nonsmooth, nonconvex $\ell_1$ minimization formulation of the problem, under mild statistical assumptions on the data. This is in contrast to previous provable methods that require either expensive computation or delicate initialization schemes. Our analysis develops several tools for characterizing landscapes of nonsmooth functions, which might be of independent interest for provable training of deep networks with nonsmooth activations (e.g., ReLU), among numerous other applications. Preliminary experiments corroborate our analysis and show that our algorithm works well empirically in recovering orthogonal dictionaries.