Global Optimization Networks

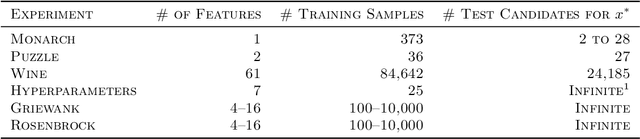
We consider the problem of estimating a good maximizer of a black-box function given noisy examples. To solve such problems, we propose to fit a new type of function which we call a global optimization network (GON), defined as any composition of an invertible function and a unimodal function, whose unique global maximizer can be inferred in $\mathcal{O}(D)$ time. In this paper, we show how to construct invertible and unimodal functions by using linear inequality constraints on lattice models. We also extend to \emph{conditional} GONs that find a global maximizer conditioned on specified inputs of other dimensions. Experiments show the GON maximizers are statistically significantly better predictions than those produced by convex fits, GPR, or DNNs, and are more reasonable predictions for real-world problems.

Regularization Strategies for Quantile Regression

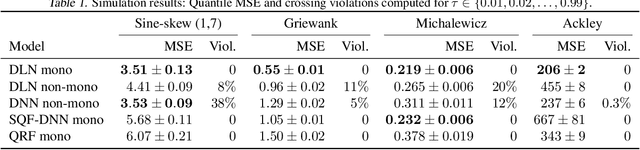
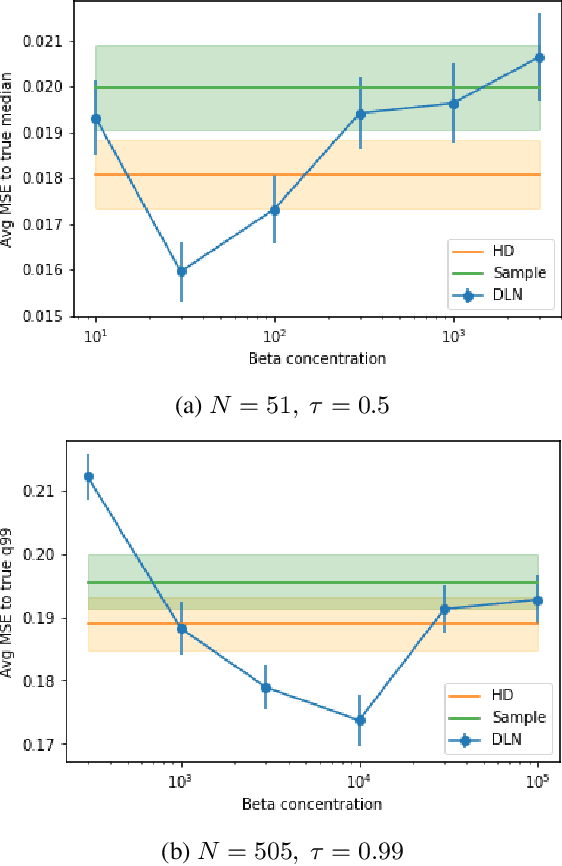
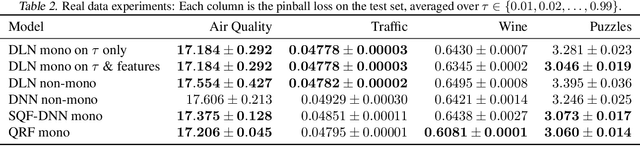
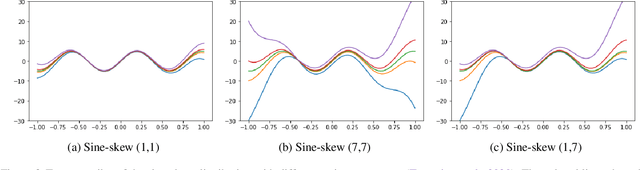
We investigate different methods for regularizing quantile regression when predicting either a subset of quantiles or the full inverse CDF. We show that minimizing an expected pinball loss over a continuous distribution of quantiles is a good regularizer even when only predicting a specific quantile. For predicting multiple quantiles, we propose achieving the classic goal of non-crossing quantiles by using deep lattice networks that treat the quantile as a monotonic input feature, and we discuss why monotonicity on other features is an apt regularizer for quantile regression. We show that lattice models enable regularizing the predicted distribution to a location-scale family. Lastly, we propose applying rate constraints to improve the calibration of the quantile predictions on specific subsets of interest and improve fairness metrics. We demonstrate our contributions on simulations, benchmark datasets, and real quantile regression problems.

Deep k-NN for Noisy Labels

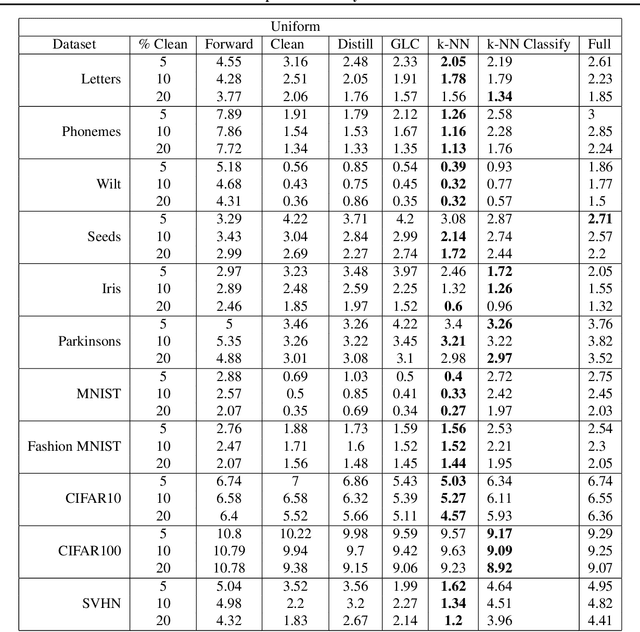
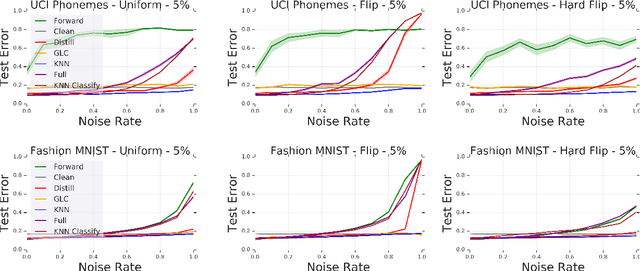
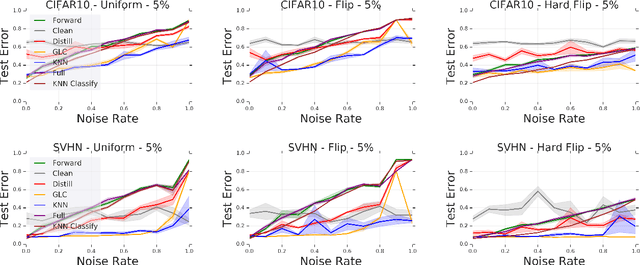
Modern machine learning models are often trained on examples with noisy labels that hurt performance and are hard to identify. In this paper, we provide an empirical study showing that a simple $k$-nearest neighbor-based filtering approach on the logit layer of a preliminary model can remove mislabeled training data and produce more accurate models than many recently proposed methods. We also provide new statistical guarantees into its efficacy.

Robust Optimization for Fairness with Noisy Protected Groups

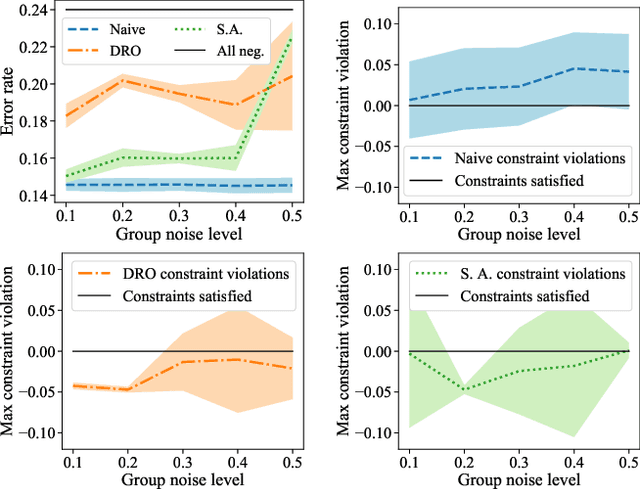
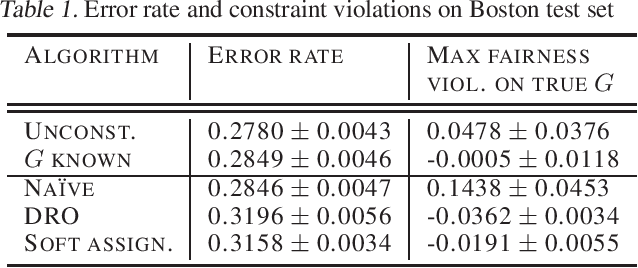
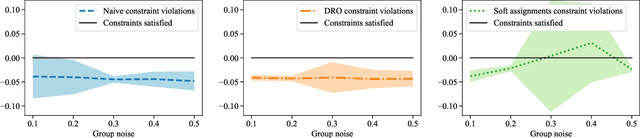
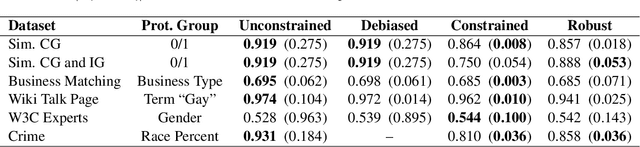
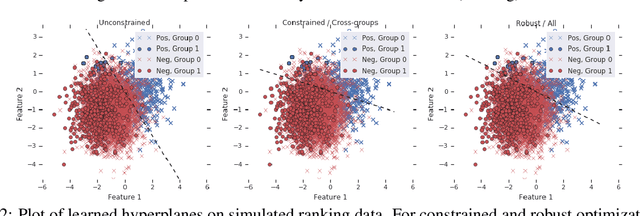
Many existing fairness criteria for machine learning involve equalizing or achieving some metric across \textit{protected groups} such as race or gender groups. However, practitioners trying to audit or enforce such group-based criteria can easily face the problem of noisy or biased protected group information. We study this important practical problem in two ways. First, we study the consequences of na{\"i}vely only relying on noisy protected groups: we provide an upper bound on the fairness violations on the true groups $G$ when the fairness criteria are satisfied on noisy groups $\hat{G}$. Second, we introduce two new approaches using robust optimization that, unlike the na{\"i}ve approach of only relying on $\hat{G}$, are guaranteed to satisfy fairness criteria on the true protected groups $G$ while minimizing a training objective. We provide theoretical guarantees that one such approach converges to an optimal feasible solution. Using two case studies, we empirically show that the robust approaches achieve better true group fairness guarantees than the na{\"i}ve approach.

Optimizing Black-box Metrics with Adaptive Surrogates

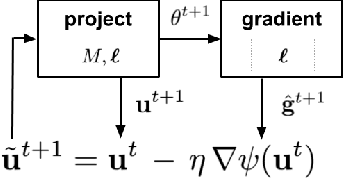
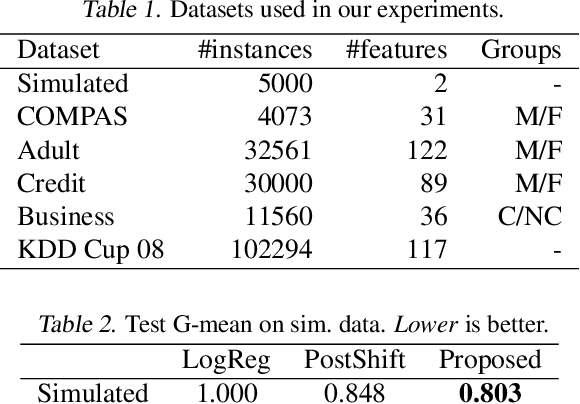
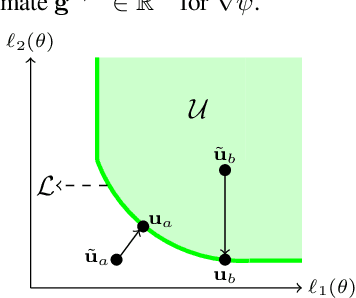
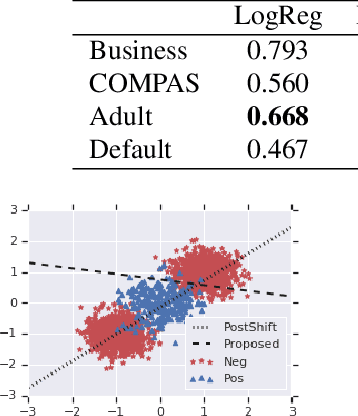
We address the problem of training models with black-box and hard-to-optimize metrics by expressing the metric as a monotonic function of a small number of easy-to-optimize surrogates. We pose the training problem as an optimization over a relaxed surrogate space, which we solve by estimating local gradients for the metric and performing inexact convex projections. We analyze gradient estimates based on finite differences and local linear interpolations, and show convergence of our approach under smoothness assumptions with respect to the surrogates. Experimental results on classification and ranking problems verify the proposal performs on par with methods that know the mathematical formulation, and adds notable value when the form of the metric is unknown.

Deontological Ethics By Monotonicity Shape Constraints

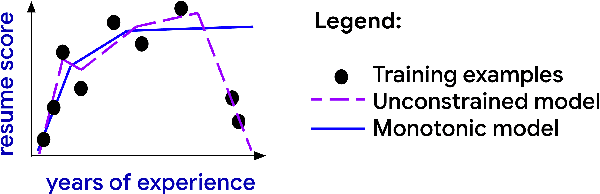
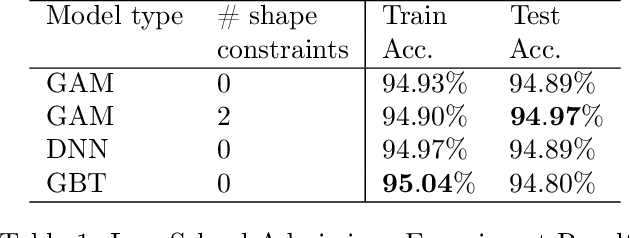
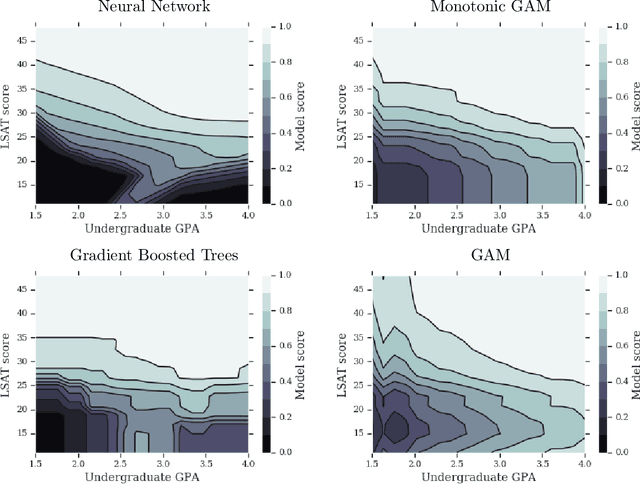
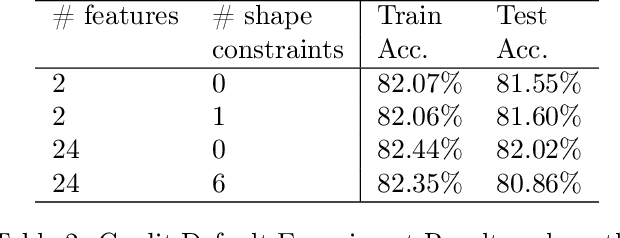
We demonstrate how easy it is for modern machine-learned systems to violate common deontological ethical principles and social norms such as "favor the less fortunate", and "do not penalize good attributes." We propose that in some cases such ethical principles can be incorporated into a machine-learned model by adding shape constraints that constrain the model to respond only positively to relevant inputs. We analyze the relationship between these deontological constraints that act on individuals and the consequentialist group-based fairness goals of one-sided statistical parity and equal opportunity. This strategy works with sensitive attributes that are Boolean or real-valued such as income and age, and can help produce more responsible and trustworthy AI.

Optimizing Generalized Rate Metrics through Game Equilibrium

We present a general framework for solving a large class of learning problems with non-linear functions of classification rates. This includes problems where one wishes to optimize a non-decomposable performance metric such as the F-measure or G-mean, and constrained training problems where the classifier needs to satisfy non-linear rate constraints such as predictive parity fairness, distribution divergences or churn ratios. We extend previous two-player game approaches for constrained optimization to a game between three players to decouple the classifier rates from the non-linear objective, and seek to find an equilibrium of the game. Our approach generalizes many existing algorithms, and makes possible new algorithms with more flexibility and tighter handling of non-linear rate constraints. We provide convergence guarantees for convex functions of rates, and show how our methodology can be extended to handle sums of ratios of rates. Experiments on different fairness tasks confirm the efficacy of our approach.

Pairwise Fairness for Ranking and Regression

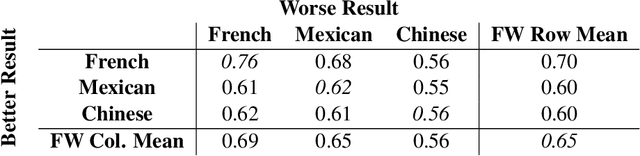
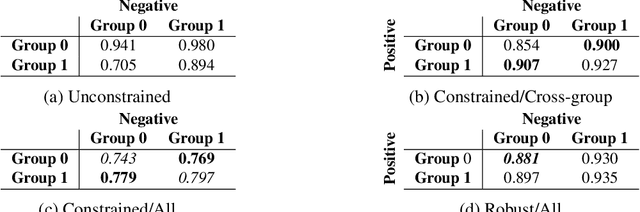
We present pairwise metrics of fairness for ranking and regression models that form analogues of statistical fairness notions such as equal opportunity or equal accuracy, as well as statistical parity. Our pairwise formulation supports both discrete protected groups, and continuous protected attributes. We show that the resulting training problems can be efficiently and effectively solved using constrained optimization and robust optimization techniques based on two player game algorithms developed for fair classification. Experiments illustrate the broad applicability and trade-offs of these methods.

Minimum-Margin Active Learning

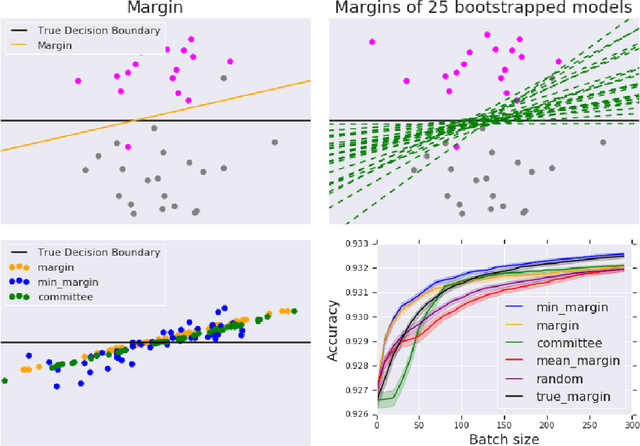
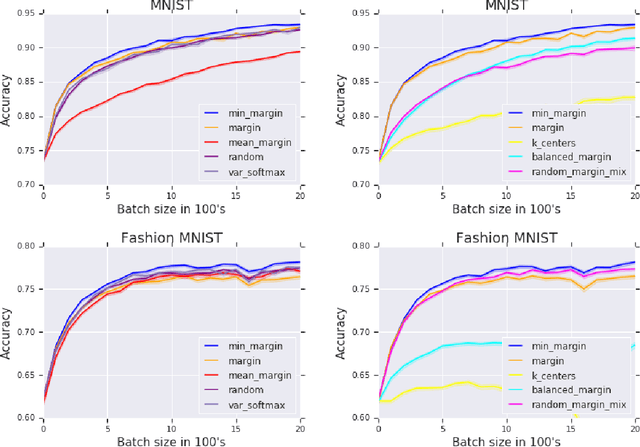
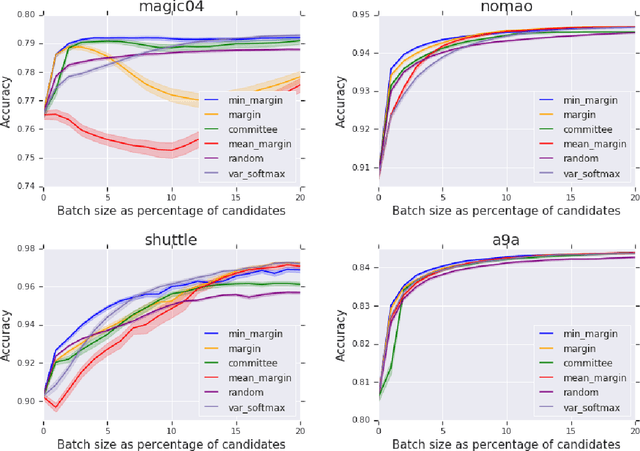
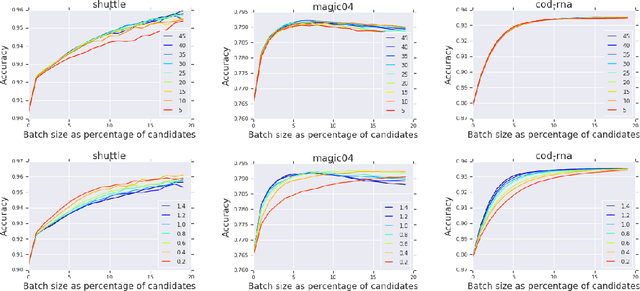
We present a new active sampling method we call min-margin which trains multiple learners on bootstrap samples and then chooses the examples to label based on the candidates' minimum margin amongst the bootstrapped models. This extends standard margin sampling in a way that increases its diversity in a supervised manner as it arises from the model uncertainty. We focus on the one-shot batch active learning setting, and show theoretically and through extensive experiments on a broad set of problems that min-margin outperforms other methods, particularly as batch size grows.

To Trust Or Not To Trust A Classifier

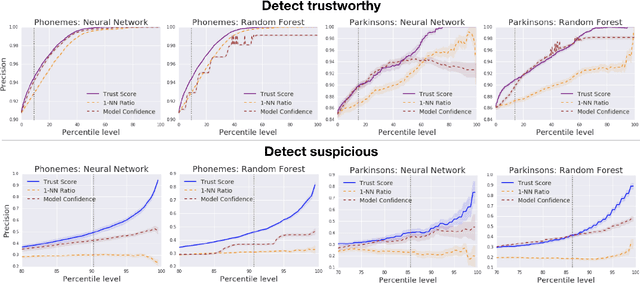
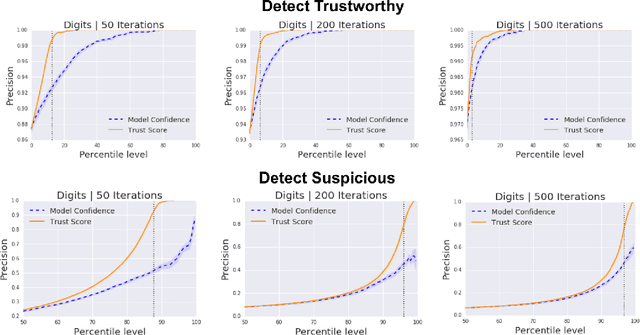
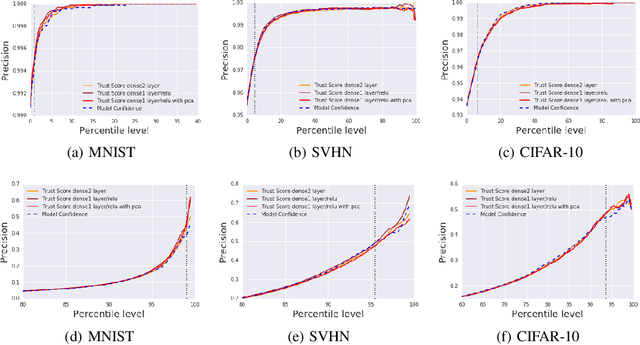
Knowing when a classifier's prediction can be trusted is useful in many applications and critical for safely using AI. While the bulk of the effort in machine learning research has been towards improving classifier performance, understanding when a classifier's predictions should and should not be trusted has received far less attention. The standard approach is to use the classifier's discriminant or confidence score; however, we show there exists an alternative that is more effective in many situations. We propose a new score, called the trust score, which measures the agreement between the classifier and a modified nearest-neighbor classifier on the testing example. We show empirically that high (low) trust scores produce surprisingly high precision at identifying correctly (incorrectly) classified examples, consistently outperforming the classifier's confidence score as well as many other baselines. Further, under some mild distributional assumptions, we show that if the trust score for an example is high (low), the classifier will likely agree (disagree) with the Bayes-optimal classifier. Our guarantees consist of non-asymptotic rates of statistical consistency under various nonparametric settings and build on recent developments in topological data analysis.