To Trust Or Not To Trust A Classifier
Paper and Code
Oct 26, 2018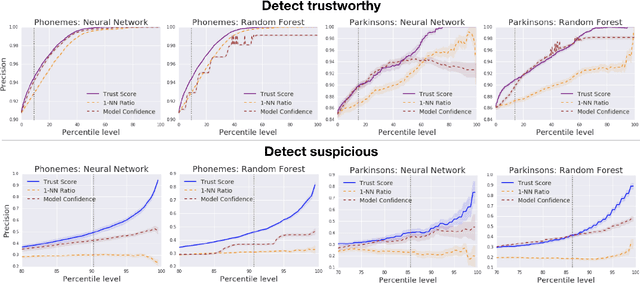
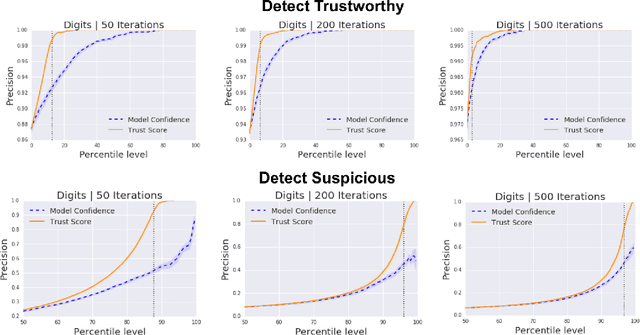
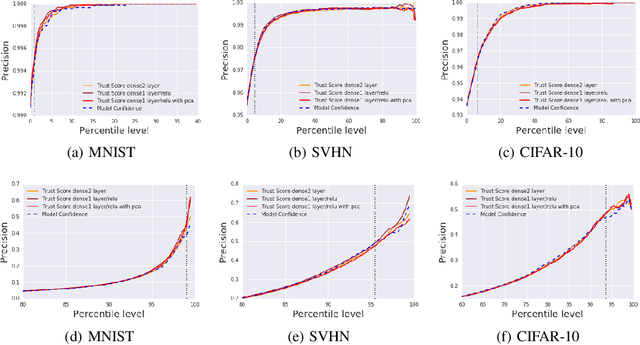
Knowing when a classifier's prediction can be trusted is useful in many applications and critical for safely using AI. While the bulk of the effort in machine learning research has been towards improving classifier performance, understanding when a classifier's predictions should and should not be trusted has received far less attention. The standard approach is to use the classifier's discriminant or confidence score; however, we show there exists an alternative that is more effective in many situations. We propose a new score, called the trust score, which measures the agreement between the classifier and a modified nearest-neighbor classifier on the testing example. We show empirically that high (low) trust scores produce surprisingly high precision at identifying correctly (incorrectly) classified examples, consistently outperforming the classifier's confidence score as well as many other baselines. Further, under some mild distributional assumptions, we show that if the trust score for an example is high (low), the classifier will likely agree (disagree) with the Bayes-optimal classifier. Our guarantees consist of non-asymptotic rates of statistical consistency under various nonparametric settings and build on recent developments in topological data analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge