Predicting on the Edge: Identifying Where a Larger Model Does Better

Much effort has been devoted to making large and more accurate models, but relatively little has been put into understanding which examples are benefiting from the added complexity. In this paper, we demonstrate and analyze the surprisingly tight link between a model's predictive uncertainty on individual examples and the likelihood that larger models will improve prediction on them. Through extensive numerical studies on the T5 encoder-decoder architecture, we show that large models have the largest improvement on examples where the small model is most uncertain. On more certain examples, even those where the small model is not particularly accurate, large models are often unable to improve at all, and can even perform worse than the smaller model. Based on these findings, we show that a switcher model which defers examples to a larger model when a small model is uncertain can achieve striking improvements in performance and resource usage. We also explore committee-based uncertainty metrics that can be more effective but less practical.

Regularization Strategies for Quantile Regression

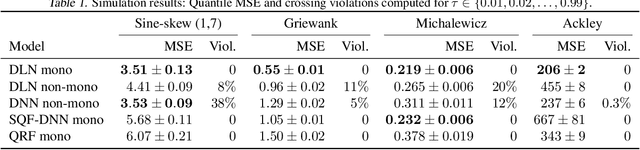
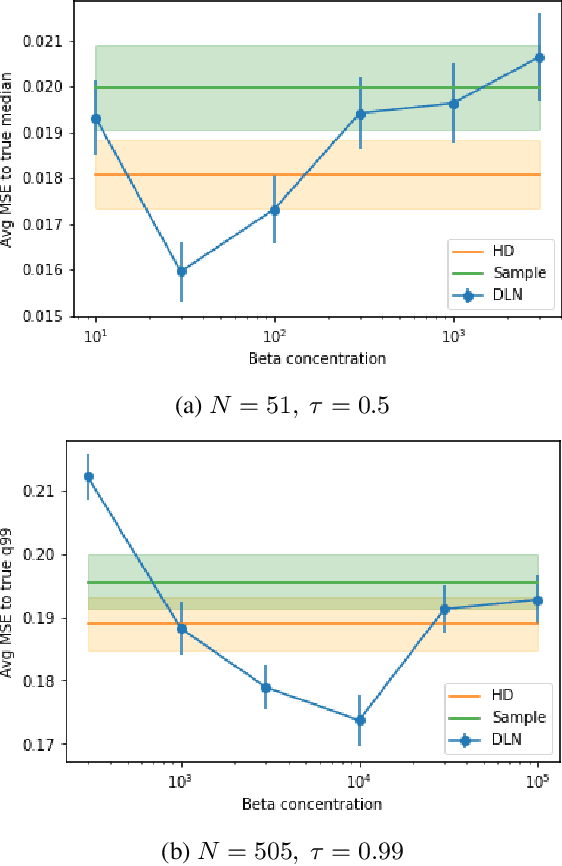
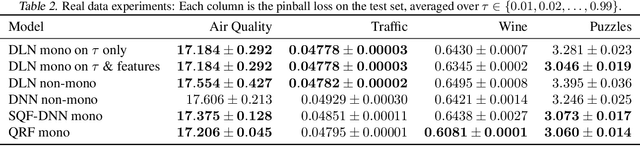
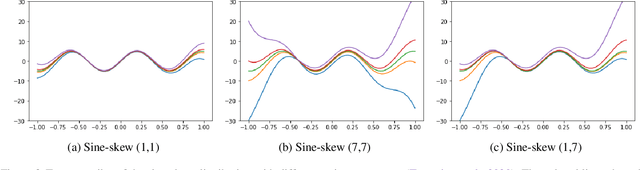
We investigate different methods for regularizing quantile regression when predicting either a subset of quantiles or the full inverse CDF. We show that minimizing an expected pinball loss over a continuous distribution of quantiles is a good regularizer even when only predicting a specific quantile. For predicting multiple quantiles, we propose achieving the classic goal of non-crossing quantiles by using deep lattice networks that treat the quantile as a monotonic input feature, and we discuss why monotonicity on other features is an apt regularizer for quantile regression. We show that lattice models enable regularizing the predicted distribution to a location-scale family. Lastly, we propose applying rate constraints to improve the calibration of the quantile predictions on specific subsets of interest and improve fairness metrics. We demonstrate our contributions on simulations, benchmark datasets, and real quantile regression problems.

Optimization with Non-Differentiable Constraints with Applications to Fairness, Recall, Churn, and Other Goals

We show that many machine learning goals, such as improved fairness metrics, can be expressed as constraints on the model's predictions, which we call rate constraints. We study the problem of training non-convex models subject to these rate constraints (or any non-convex and non-differentiable constraints). In the non-convex setting, the standard approach of Lagrange multipliers may fail. Furthermore, if the constraints are non-differentiable, then one cannot optimize the Lagrangian with gradient-based methods. To solve these issues, we introduce the proxy-Lagrangian formulation. This new formulation leads to an algorithm that produces a stochastic classifier by playing a two-player non-zero-sum game solving for what we call a semi-coarse correlated equilibrium, which in turn corresponds to an approximately optimal and feasible solution to the constrained optimization problem. We then give a procedure which shrinks the randomized solution down to one that is a mixture of at most $m+1$ deterministic solutions, given $m$ constraints. This culminates in algorithms that can solve non-convex constrained optimization problems with possibly non-differentiable and non-convex constraints with theoretical guarantees. We provide extensive experimental results enforcing a wide range of policy goals including different fairness metrics, and other goals on accuracy, coverage, recall, and churn.

Interpretable Set Functions

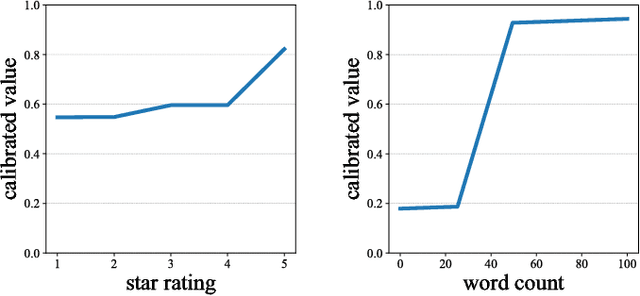
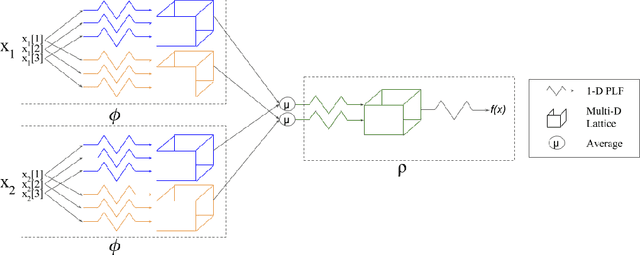
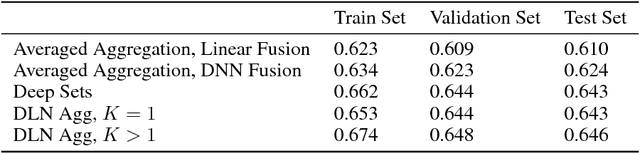
We propose learning flexible but interpretable functions that aggregate a variable-length set of permutation-invariant feature vectors to predict a label. We use a deep lattice network model so we can architect the model structure to enhance interpretability, and add monotonicity constraints between inputs-and-outputs. We then use the proposed set function to automate the engineering of dense, interpretable features from sparse categorical features, which we call semantic feature engine. Experiments on real-world data show the achieved accuracy is similar to deep sets or deep neural networks, and is easier to debug and understand.