Regularization Strategies for Quantile Regression
Paper and Code
Feb 09, 2021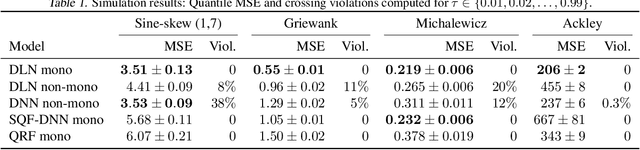
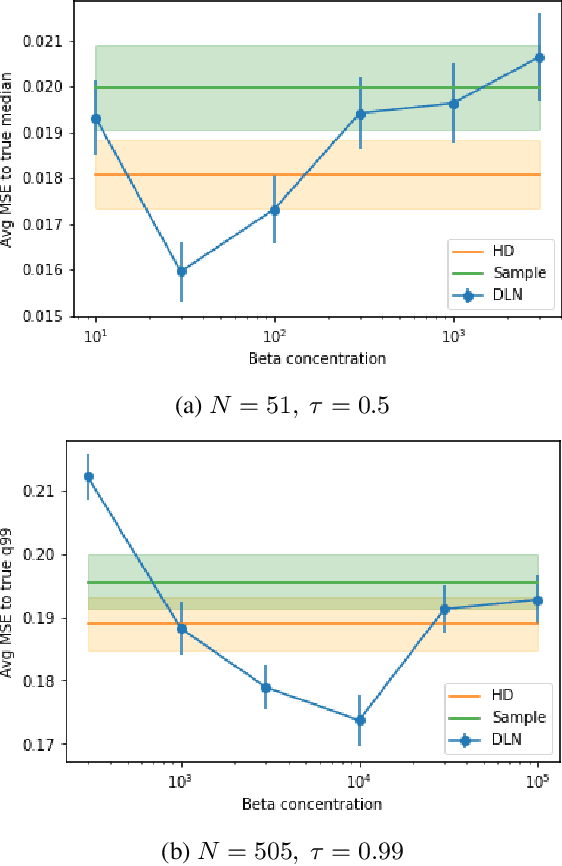
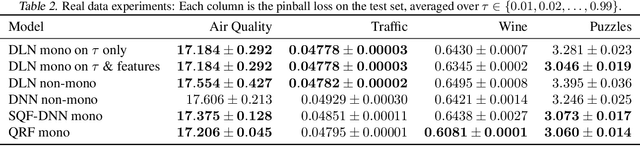
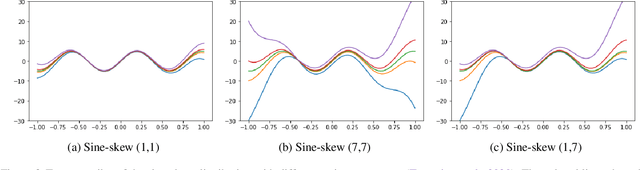
We investigate different methods for regularizing quantile regression when predicting either a subset of quantiles or the full inverse CDF. We show that minimizing an expected pinball loss over a continuous distribution of quantiles is a good regularizer even when only predicting a specific quantile. For predicting multiple quantiles, we propose achieving the classic goal of non-crossing quantiles by using deep lattice networks that treat the quantile as a monotonic input feature, and we discuss why monotonicity on other features is an apt regularizer for quantile regression. We show that lattice models enable regularizing the predicted distribution to a location-scale family. Lastly, we propose applying rate constraints to improve the calibration of the quantile predictions on specific subsets of interest and improve fairness metrics. We demonstrate our contributions on simulations, benchmark datasets, and real quantile regression problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge