Regularization Strategies for Quantile Regression

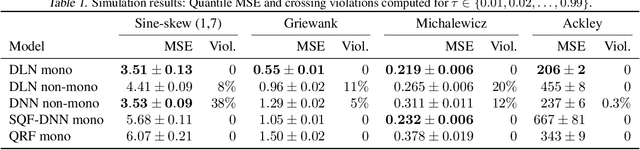
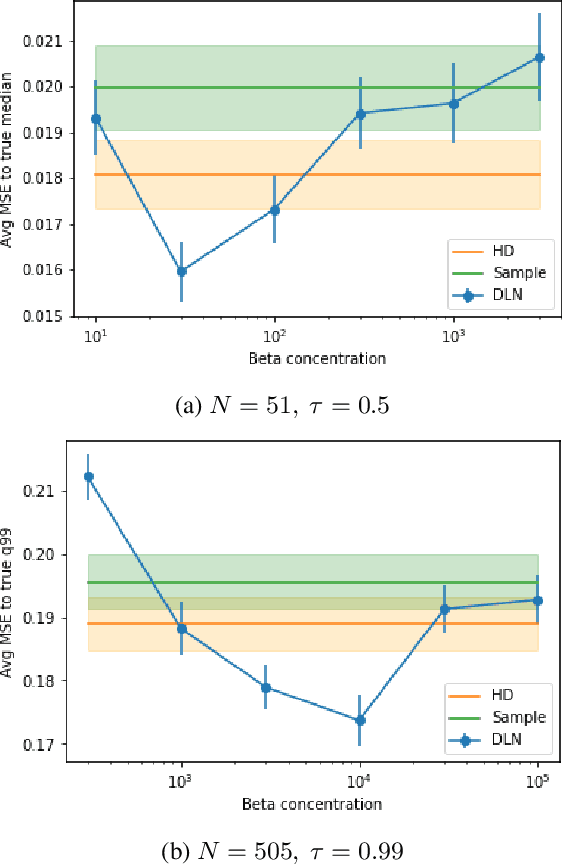
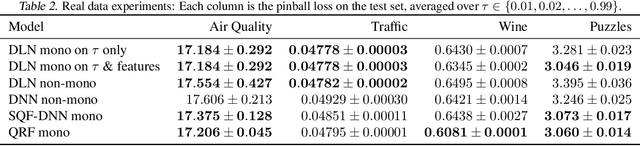
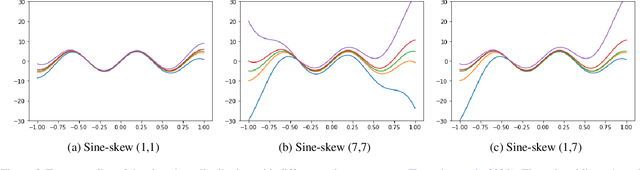
We investigate different methods for regularizing quantile regression when predicting either a subset of quantiles or the full inverse CDF. We show that minimizing an expected pinball loss over a continuous distribution of quantiles is a good regularizer even when only predicting a specific quantile. For predicting multiple quantiles, we propose achieving the classic goal of non-crossing quantiles by using deep lattice networks that treat the quantile as a monotonic input feature, and we discuss why monotonicity on other features is an apt regularizer for quantile regression. We show that lattice models enable regularizing the predicted distribution to a location-scale family. Lastly, we propose applying rate constraints to improve the calibration of the quantile predictions on specific subsets of interest and improve fairness metrics. We demonstrate our contributions on simulations, benchmark datasets, and real quantile regression problems.

Deep Lattice Networks and Partial Monotonic Functions

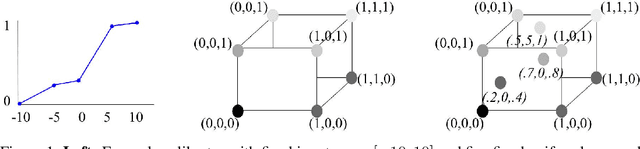
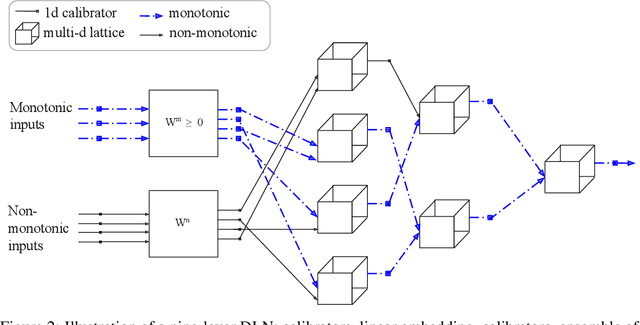
We propose learning deep models that are monotonic with respect to a user-specified set of inputs by alternating layers of linear embeddings, ensembles of lattices, and calibrators (piecewise linear functions), with appropriate constraints for monotonicity, and jointly training the resulting network. We implement the layers and projections with new computational graph nodes in TensorFlow and use the ADAM optimizer and batched stochastic gradients. Experiments on benchmark and real-world datasets show that six-layer monotonic deep lattice networks achieve state-of-the art performance for classification and regression with monotonicity guarantees.

Monotonic Calibrated Interpolated Look-Up Tables

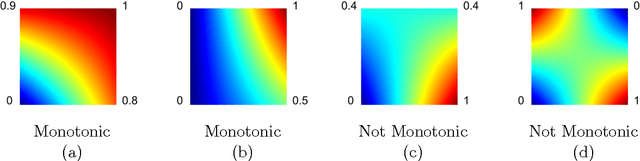
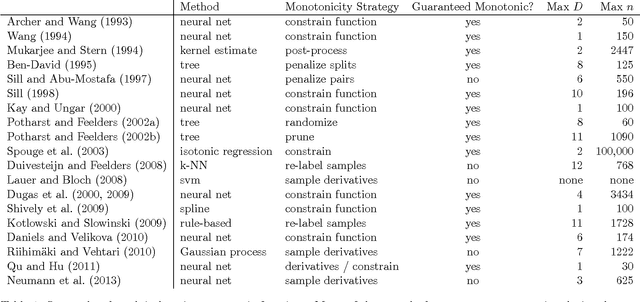
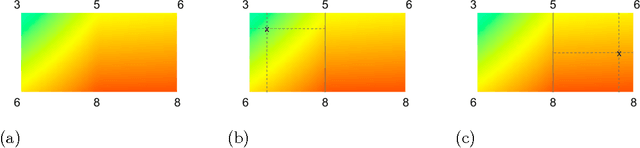
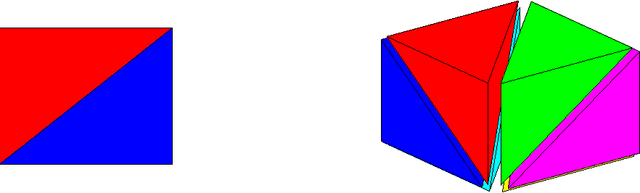
Real-world machine learning applications may require functions that are fast-to-evaluate and interpretable. In particular, guaranteed monotonicity of the learned function can be critical to user trust. We propose meeting these goals for low-dimensional machine learning problems by learning flexible, monotonic functions using calibrated interpolated look-up tables. We extend the structural risk minimization framework of lattice regression to train monotonic look-up tables by solving a convex problem with appropriate linear inequality constraints. In addition, we propose jointly learning interpretable calibrations of each feature to normalize continuous features and handle categorical or missing data, at the cost of making the objective non-convex. We address large-scale learning through parallelization, mini-batching, and propose random sampling of additive regularizer terms. Case studies with real-world problems with five to sixteen features and thousands to millions of training samples demonstrate the proposed monotonic functions can achieve state-of-the-art accuracy on practical problems while providing greater transparency to users.