Monotonic Calibrated Interpolated Look-Up Tables
Paper and Code
Jan 20, 2016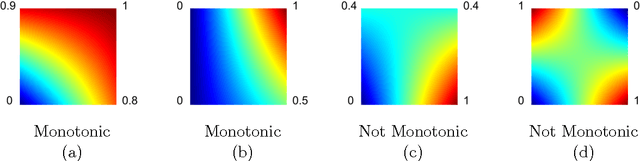
Real-world machine learning applications may require functions that are fast-to-evaluate and interpretable. In particular, guaranteed monotonicity of the learned function can be critical to user trust. We propose meeting these goals for low-dimensional machine learning problems by learning flexible, monotonic functions using calibrated interpolated look-up tables. We extend the structural risk minimization framework of lattice regression to train monotonic look-up tables by solving a convex problem with appropriate linear inequality constraints. In addition, we propose jointly learning interpretable calibrations of each feature to normalize continuous features and handle categorical or missing data, at the cost of making the objective non-convex. We address large-scale learning through parallelization, mini-batching, and propose random sampling of additive regularizer terms. Case studies with real-world problems with five to sixteen features and thousands to millions of training samples demonstrate the proposed monotonic functions can achieve state-of-the-art accuracy on practical problems while providing greater transparency to users.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge