Yggdrasil Decision Forests: A Fast and Extensible Decision Forests Library

Yggdrasil Decision Forests is a library for the training, serving and interpretation of decision forest models, targeted both at research and production work, implemented in C++, and available in C++, command line interface, Python (under the name TensorFlow Decision Forests), JavaScript, and Go. The library has been developed organically since 2018 following a set of four design principles applicable to machine learning libraries and frameworks: simplicity of use, safety of use, modularity and high-level abstraction, and integration with other machine learning libraries. In this paper, we describe those principles in detail and present how they have been used to guide the design of the library. We then showcase the use of our library on a set of classical machine learning problems. Finally, we report a benchmark comparing our library to related solutions.

TF-GNN: Graph Neural Networks in TensorFlow

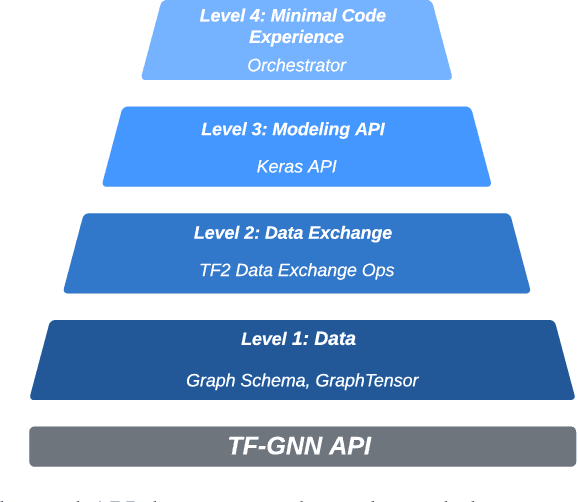
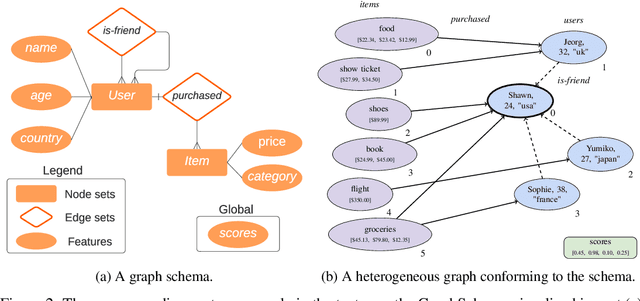
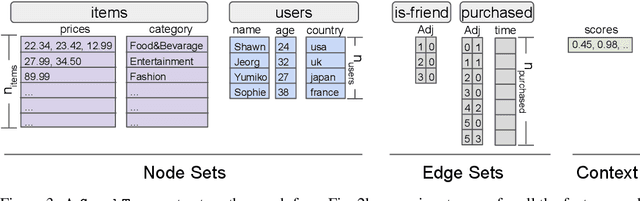
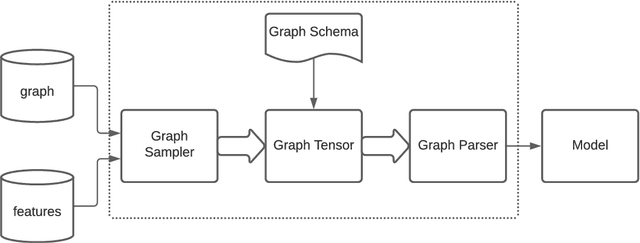
TensorFlow GNN (TF-GNN) is a scalable library for Graph Neural Networks in TensorFlow. It is designed from the bottom up to support the kinds of rich heterogeneous graph data that occurs in today's information ecosystems. Many production models at Google use TF-GNN and it has been recently released as an open source project. In this paper, we describe the TF-GNN data model, its Keras modeling API, and relevant capabilities such as graph sampling, distributed training, and accelerator support.

Modeling Text with Decision Forests using Categorical-Set Splits

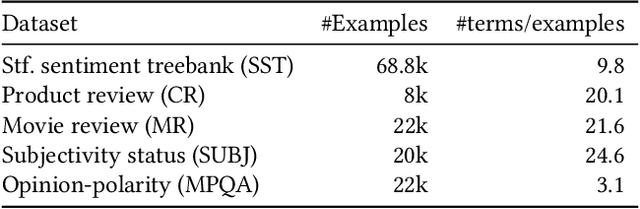
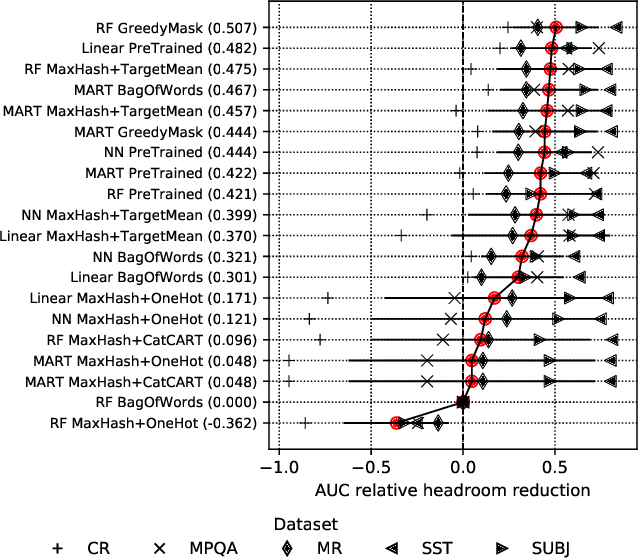
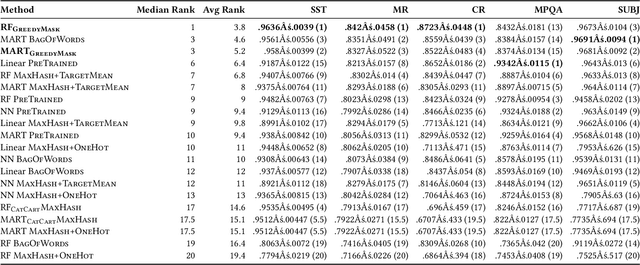
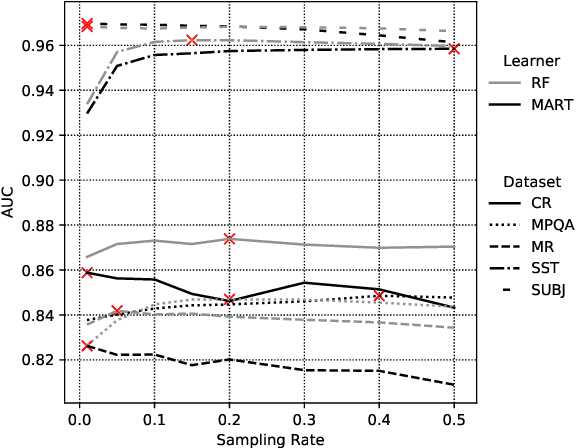
Decision forest algorithms model data by learning a binary tree structure recursively where every node splits the feature space into two regions, sending examples into the left or right branches. This "decision" is the result of the evaluation of a condition. For example, a node may split input data by applying a threshold to a numerical feature value. Such decisions are learned using (often greedy) algorithms that attempt to optimize a local loss function. Crucially, whether an algorithm exists to find and evaluate splits for a feature type (e.g., text) determines whether a decision forest algorithm can model that feature type at all. In this work, we set out to devise such an algorithm for textual features, thereby equipping decision forests with the ability to directly model text without the need for feature transformation. Our algorithm is efficient during training and the resulting splits are fast to evaluate with our extension of the QuickScorer inference algorithm. Experiments on benchmark text classification datasets demonstrate the utility and effectiveness of our proposal.

Learning Representations for Axis-Aligned Decision Forests through Input Perturbation

Axis-aligned decision forests have long been the leading class of machine learning algorithms for modeling tabular data. In many applications of machine learning such as learning-to-rank, decision forests deliver remarkable performance. They also possess other coveted characteristics such as interpretability. Despite their widespread use and rich history, decision forests to date fail to consume raw structured data such as text, or learn effective representations for them, a factor behind the success of deep neural networks in recent years. While there exist methods that construct smoothed decision forests to achieve representation learning, the resulting models are decision forests in name only: They are no longer axis-aligned, use stochastic decisions, or are not interpretable. Furthermore, none of the existing methods are appropriate for problems that require a Transfer Learning treatment. In this work, we present a novel but intuitive proposal to achieve representation learning for decision forests without imposing new restrictions or necessitating structural changes. Our model is simply a decision forest, possibly trained using any forest learning algorithm, atop a deep neural network. By approximating the gradients of the decision forest through input perturbation, a purely analytical procedure, the decision forest directs the neural network to learn or fine-tune representations. Our framework has the advantage that it is applicable to any arbitrary decision forest and that it allows the use of arbitrary deep neural networks for representation learning. We demonstrate the feasibility and effectiveness of our proposal through experiments on synthetic and benchmark classification datasets.

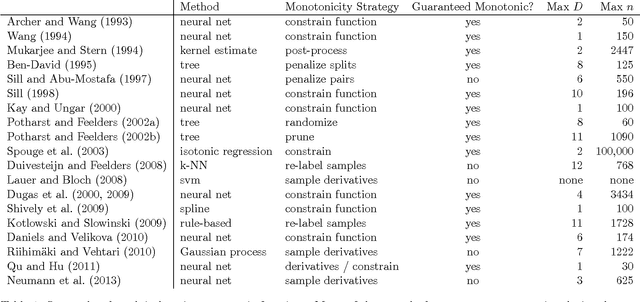
Deep Lattice Networks and Partial Monotonic Functions

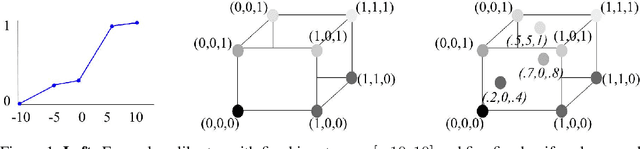
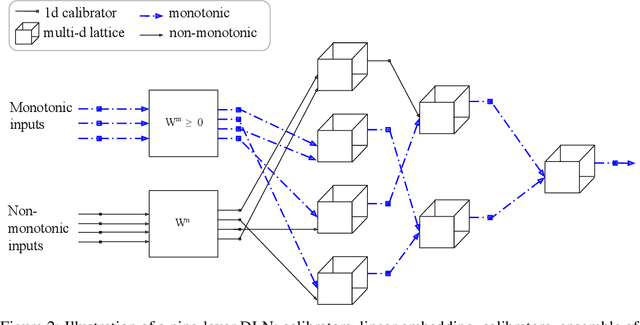
We propose learning deep models that are monotonic with respect to a user-specified set of inputs by alternating layers of linear embeddings, ensembles of lattices, and calibrators (piecewise linear functions), with appropriate constraints for monotonicity, and jointly training the resulting network. We implement the layers and projections with new computational graph nodes in TensorFlow and use the ADAM optimizer and batched stochastic gradients. Experiments on benchmark and real-world datasets show that six-layer monotonic deep lattice networks achieve state-of-the art performance for classification and regression with monotonicity guarantees.

A Light Touch for Heavily Constrained SGD

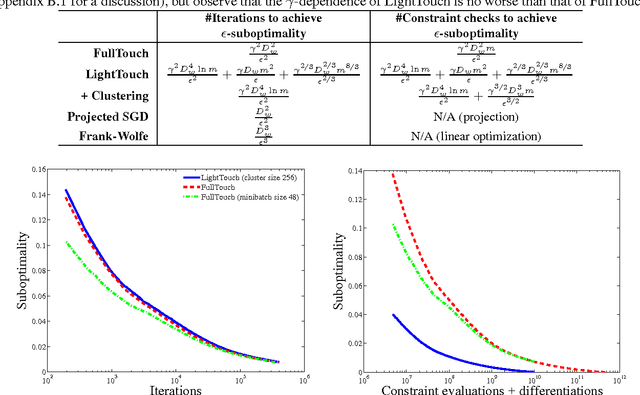
Minimizing empirical risk subject to a set of constraints can be a useful strategy for learning restricted classes of functions, such as monotonic functions, submodular functions, classifiers that guarantee a certain class label for some subset of examples, etc. However, these restrictions may result in a very large number of constraints. Projected stochastic gradient descent (SGD) is often the default choice for large-scale optimization in machine learning, but requires a projection after each update. For heavily-constrained objectives, we propose an efficient extension of SGD that stays close to the feasible region while only applying constraints probabilistically at each iteration. Theoretical analysis shows a compelling trade-off between per-iteration work and the number of iterations needed on problems with a large number of constraints.

Monotonic Calibrated Interpolated Look-Up Tables

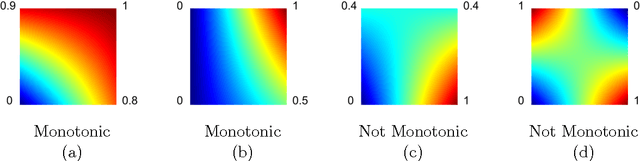
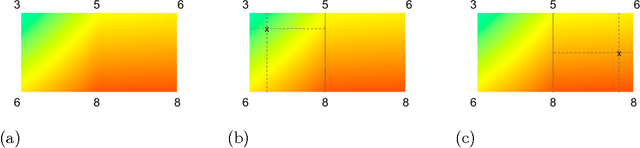
Real-world machine learning applications may require functions that are fast-to-evaluate and interpretable. In particular, guaranteed monotonicity of the learned function can be critical to user trust. We propose meeting these goals for low-dimensional machine learning problems by learning flexible, monotonic functions using calibrated interpolated look-up tables. We extend the structural risk minimization framework of lattice regression to train monotonic look-up tables by solving a convex problem with appropriate linear inequality constraints. In addition, we propose jointly learning interpretable calibrations of each feature to normalize continuous features and handle categorical or missing data, at the cost of making the objective non-convex. We address large-scale learning through parallelization, mini-batching, and propose random sampling of additive regularizer terms. Case studies with real-world problems with five to sixteen features and thousands to millions of training samples demonstrate the proposed monotonic functions can achieve state-of-the-art accuracy on practical problems while providing greater transparency to users.