CardBench: A Benchmark for Learned Cardinality Estimation in Relational Databases

Cardinality estimation is crucial for enabling high query performance in relational databases. Recently learned cardinality estimation models have been proposed to improve accuracy but there is no systematic benchmark or datasets which allows researchers to evaluate the progress made by new learned approaches and even systematically develop new learned approaches. In this paper, we are releasing a benchmark, containing thousands of queries over 20 distinct real-world databases for learned cardinality estimation. In contrast to other initial benchmarks, our benchmark is much more diverse and can be used for training and testing learned models systematically. Using this benchmark, we explored whether learned cardinality estimation can be transferred to an unseen dataset in a zero-shot manner. We trained GNN-based and transformer-based models to study the problem in three setups: 1-) instance-based, 2-) zero-shot, and 3-) fine-tuned. Our results show that while we get promising results for zero-shot cardinality estimation on simple single table queries; as soon as we add joins, the accuracy drops. However, we show that with fine-tuning, we can still utilize pre-trained models for cardinality estimation, significantly reducing training overheads compared to instance specific models. We are open sourcing our scripts to collect statistics, generate queries and training datasets to foster more extensive research, also from the ML community on the important problem of cardinality estimation and in particular improve on recent directions such as pre-trained cardinality estimation.

TpuGraphs: A Performance Prediction Dataset on Large Tensor Computational Graphs

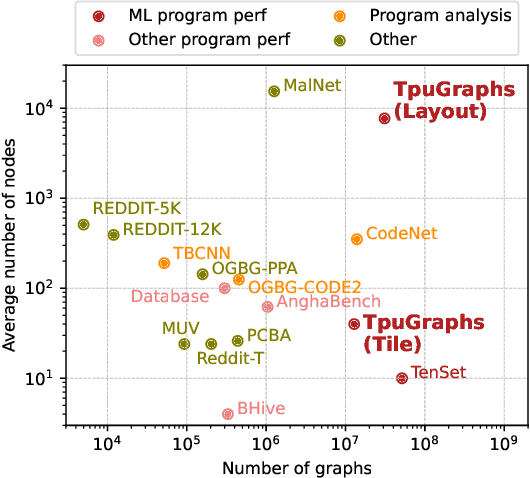
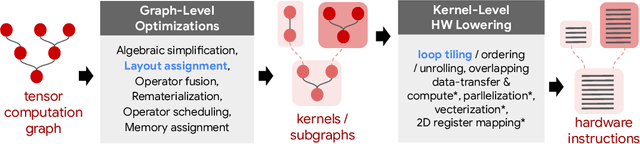
Precise hardware performance models play a crucial role in code optimizations. They can assist compilers in making heuristic decisions or aid autotuners in identifying the optimal configuration for a given program. For example, the autotuner for XLA, a machine learning compiler, discovered 10-20% speedup on state-of-the-art models serving substantial production traffic at Google. Although there exist a few datasets for program performance prediction, they target small sub-programs such as basic blocks or kernels. This paper introduces TpuGraphs, a performance prediction dataset on full tensor programs, represented as computational graphs, running on Tensor Processing Units (TPUs). Each graph in the dataset represents the main computation of a machine learning workload, e.g., a training epoch or an inference step. Each data sample contains a computational graph, a compilation configuration, and the execution time of the graph when compiled with the configuration. The graphs in the dataset are collected from open-source machine learning programs, featuring popular model architectures, e.g., ResNet, EfficientNet, Mask R-CNN, and Transformer. TpuGraphs provides 25x more graphs than the largest graph property prediction dataset (with comparable graph sizes), and 770x larger graphs on average compared to existing performance prediction datasets on machine learning programs. This graph-level prediction task on large graphs introduces new challenges in learning, ranging from scalability, training efficiency, to model quality.

UGSL: A Unified Framework for Benchmarking Graph Structure Learning

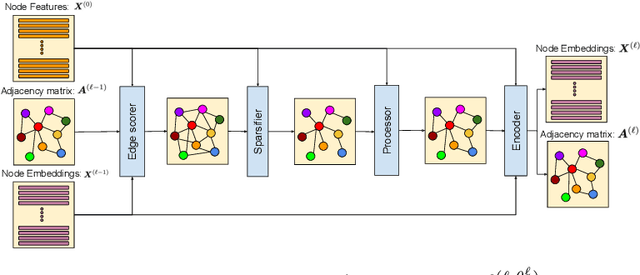
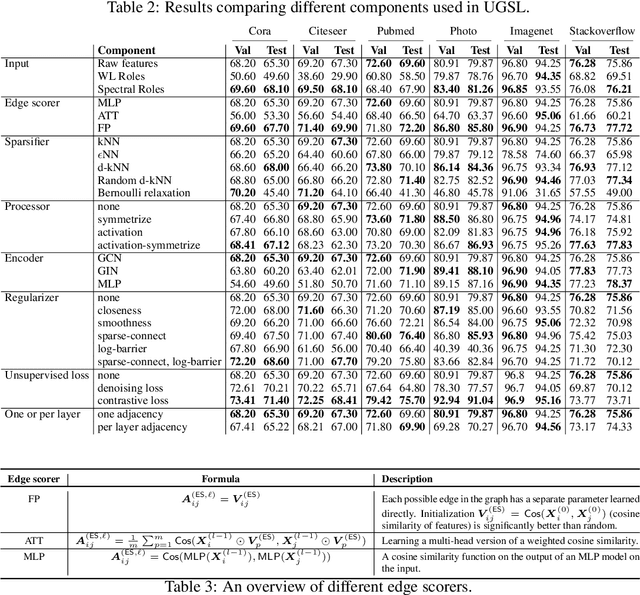
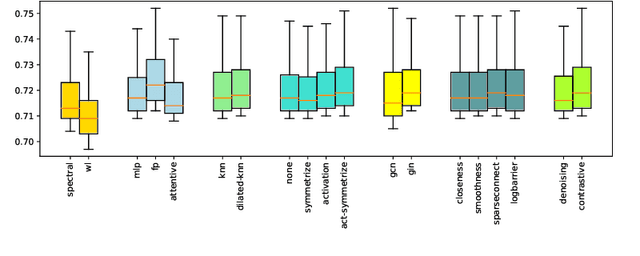
Graph neural networks (GNNs) demonstrate outstanding performance in a broad range of applications. While the majority of GNN applications assume that a graph structure is given, some recent methods substantially expanded the applicability of GNNs by showing that they may be effective even when no graph structure is explicitly provided. The GNN parameters and a graph structure are jointly learned. Previous studies adopt different experimentation setups, making it difficult to compare their merits. In this paper, we propose a benchmarking strategy for graph structure learning using a unified framework. Our framework, called Unified Graph Structure Learning (UGSL), reformulates existing models into a single model. We implement a wide range of existing models in our framework and conduct extensive analyses of the effectiveness of different components in the framework. Our results provide a clear and concise understanding of the different methods in this area as well as their strengths and weaknesses. The benchmark code is available at https://github.com/google-research/google-research/tree/master/ugsl.

Learning Large Graph Property Prediction via Graph Segment Training

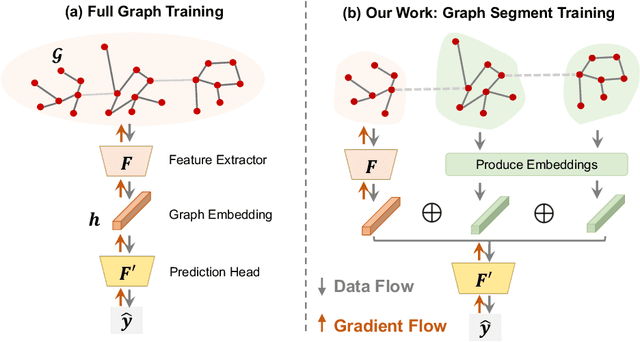
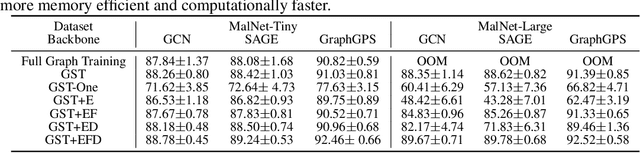
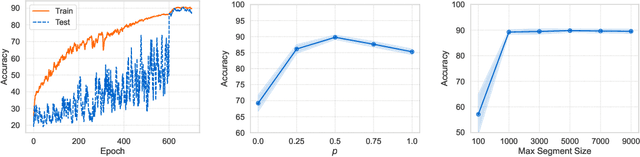
Learning to predict properties of large graphs is challenging because each prediction requires the knowledge of an entire graph, while the amount of memory available during training is bounded. Here we propose Graph Segment Training (GST), a general framework that utilizes a divide-and-conquer approach to allow learning large graph property prediction with a constant memory footprint. GST first divides a large graph into segments and then backpropagates through only a few segments sampled per training iteration. We refine the GST paradigm by introducing a historical embedding table to efficiently obtain embeddings for segments not sampled for backpropagation. To mitigate the staleness of historical embeddings, we design two novel techniques. First, we finetune the prediction head to fix the input distribution shift. Second, we introduce Stale Embedding Dropout to drop some stale embeddings during training to reduce bias. We evaluate our complete method GST-EFD (with all the techniques together) on two large graph property prediction benchmarks: MalNet and TpuGraphs. Our experiments show that GST-EFD is both memory-efficient and fast, while offering a slight boost on test accuracy over a typical full graph training regime.

TF-GNN: Graph Neural Networks in TensorFlow

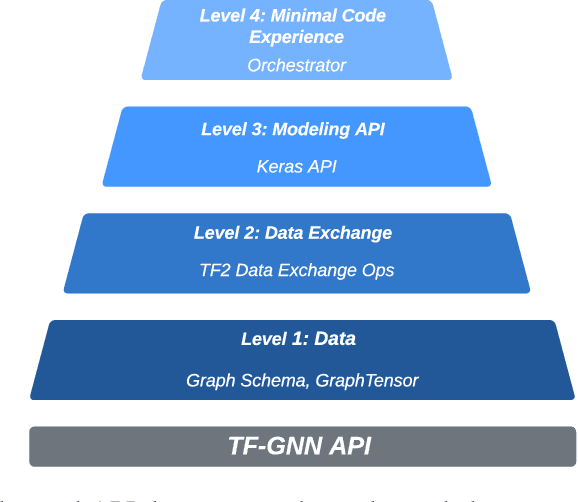
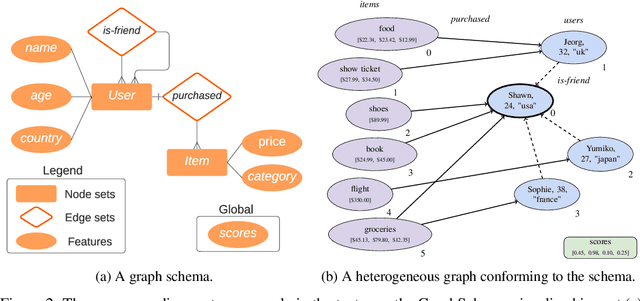
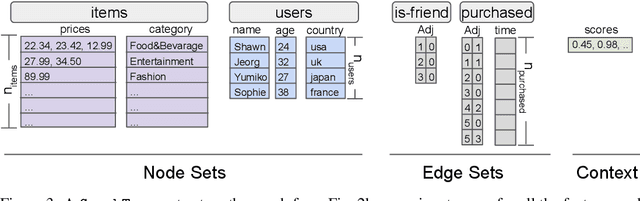
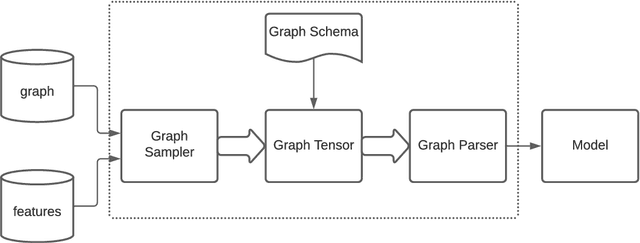
TensorFlow GNN (TF-GNN) is a scalable library for Graph Neural Networks in TensorFlow. It is designed from the bottom up to support the kinds of rich heterogeneous graph data that occurs in today's information ecosystems. Many production models at Google use TF-GNN and it has been recently released as an open source project. In this paper, we describe the TF-GNN data model, its Keras modeling API, and relevant capabilities such as graph sampling, distributed training, and accelerator support.

Implicit SVD for Graph Representation Learning

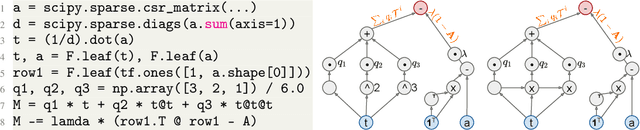
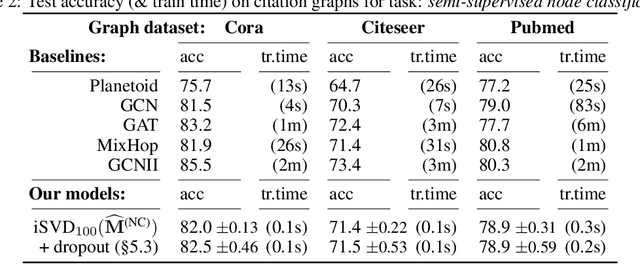
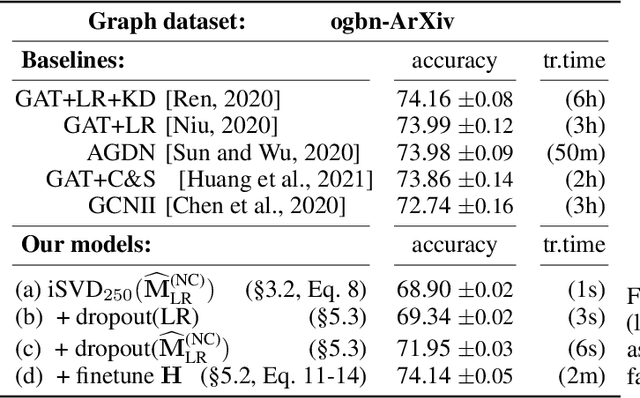
Recent improvements in the performance of state-of-the-art (SOTA) methods for Graph Representational Learning (GRL) have come at the cost of significant computational resource requirements for training, e.g., for calculating gradients via backprop over many data epochs. Meanwhile, Singular Value Decomposition (SVD) can find closed-form solutions to convex problems, using merely a handful of epochs. In this paper, we make GRL more computationally tractable for those with modest hardware. We design a framework that computes SVD of \textit{implicitly} defined matrices, and apply this framework to several GRL tasks. For each task, we derive linear approximation of a SOTA model, where we design (expensive-to-store) matrix $\mathbf{M}$ and train the model, in closed-form, via SVD of $\mathbf{M}$, without calculating entries of $\mathbf{M}$. By converging to a unique point in one step, and without calculating gradients, our models show competitive empirical test performance over various graphs such as article citation and biological interaction networks. More importantly, SVD can initialize a deeper model, that is architected to be non-linear almost everywhere, though behaves linearly when its parameters reside on a hyperplane, onto which SVD initializes. The deeper model can then be fine-tuned within only a few epochs. Overall, our procedure trains hundreds of times faster than state-of-the-art methods, while competing on empirical test performance. We open-source our implementation at: https://github.com/samihaija/isvd

Fast Graph Learning with Unique Optimal Solutions

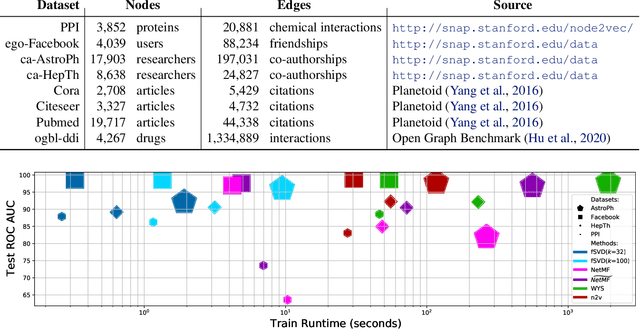
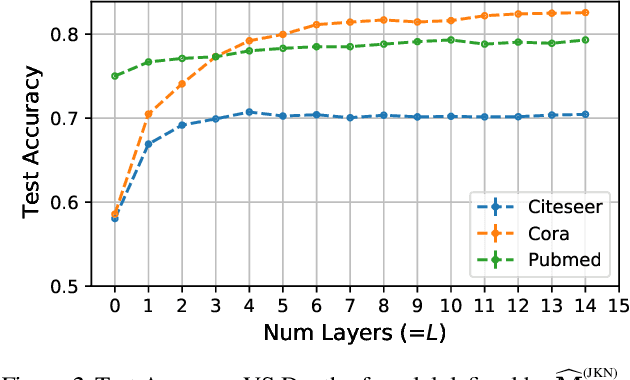
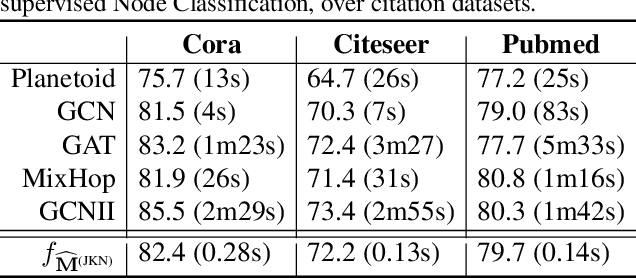
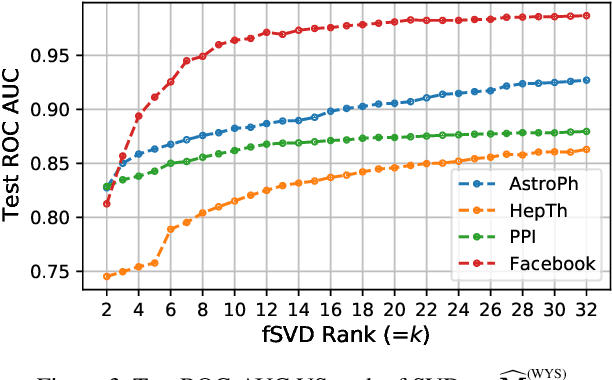
Graph Representation Learning (GRL) has been advancing at an unprecedented rate. However, many results rely on careful design and tuning of architectures, objectives, and training schemes. We propose efficient GRL methods that optimize convexified objectives with known closed form solutions. Guaranteed convergence to a global optimum releases practitioners from hyper-parameter and architecture tuning. Nevertheless, our proposed method achieves competitive or state-of-the-art performance on popular GRL tasks while providing orders of magnitude speedup. Although the design matrix ($\mathbf{M}$) of our objective is expensive to compute, we exploit results from random matrix theory to approximate solutions in linear time while avoiding an explicit calculation of $\mathbf{M}$. Our code is online: http://github.com/samihaija/tf-fsvd

Graph Traversal with Tensor Functionals: A Meta-Algorithm for Scalable Learning

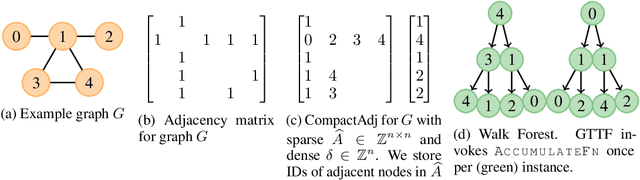
Graph Representation Learning (GRL) methods have impacted fields from chemistry to social science. However, their algorithmic implementations are specialized to specific use-cases e.g.message passing methods are run differently from node embedding ones. Despite their apparent differences, all these methods utilize the graph structure, and therefore, their learning can be approximated with stochastic graph traversals. We propose Graph Traversal via Tensor Functionals(GTTF), a unifying meta-algorithm framework for easing the implementation of diverse graph algorithms and enabling transparent and efficient scaling to large graphs. GTTF is founded upon a data structure (stored as a sparse tensor) and a stochastic graph traversal algorithm (described using tensor operations). The algorithm is a functional that accept two functions, and can be specialized to obtain a variety of GRL models and objectives, simply by changing those two functions. We show for a wide class of methods, our algorithm learns in an unbiased fashion and, in expectation, approximates the learning as if the specialized implementations were run directly. With these capabilities, we scale otherwise non-scalable methods to set state-of-the-art on large graph datasets while being more efficient than existing GRL libraries - with only a handful of lines of code for each method specialization. GTTF and its various GRL implementations are on: https://github.com/isi-usc-edu/gttf.

Zero-shot Synthesis with Group-Supervised Learning

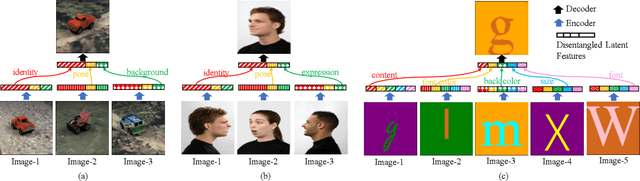
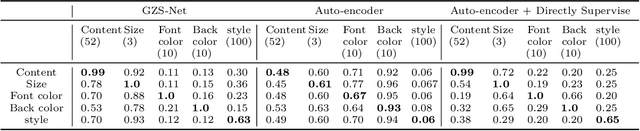
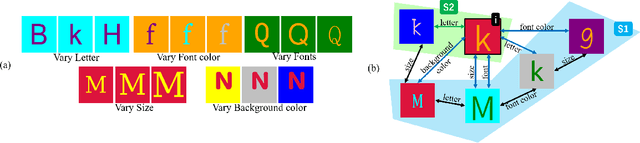
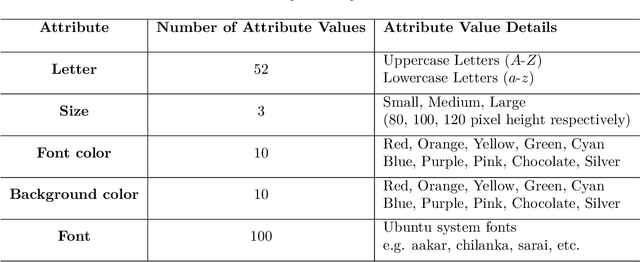
Visual cognition of primates is superior to that of artificial neural networks in its ability to 'envision' a visual object, even a newly-introduced one, in different attributes including pose, position, color, texture, etc. To aid neural networks to envision objects with different attributes, we propose a family of objective functions, expressed on groups of examples, as a novel learning framework that we term Group-Supervised Learning (GSL). GSL decomposes inputs into a disentangled representation with swappable components that can be recombined to synthesize new samples, trained through similarity mining within groups of exemplars. For instance, images of red boats & blue cars can be decomposed and recombined to synthesize novel images of red cars. We describe a general class of datasets admissible by GSL. We propose an implementation based on auto-encoder, termed group-supervised zero-shot synthesis network (GZS-Net) trained with our learning framework, that can produce a high-quality red car even if no such example is witnessed during training. We test our model and learning framework on existing benchmarks, in addition to new dataset that we open-source. We qualitatively and quantitatively demonstrate that GZS-Net trained with GSL outperforms state-of-the-art methods

End-to-end Learning of Compressible Features

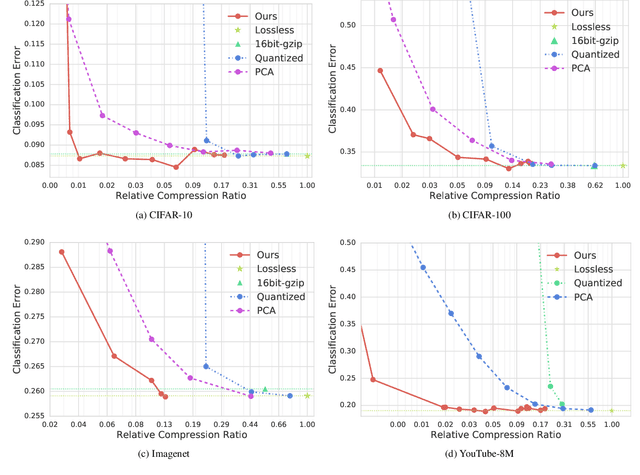
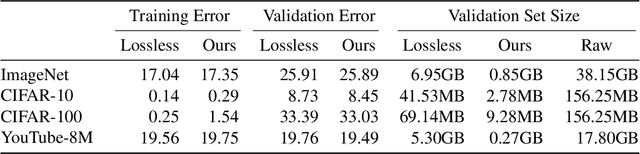
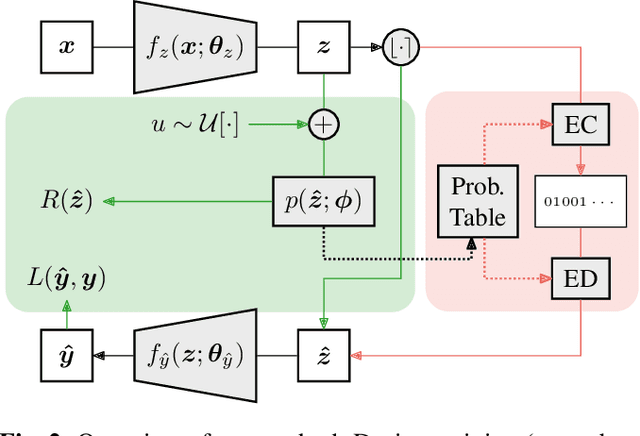
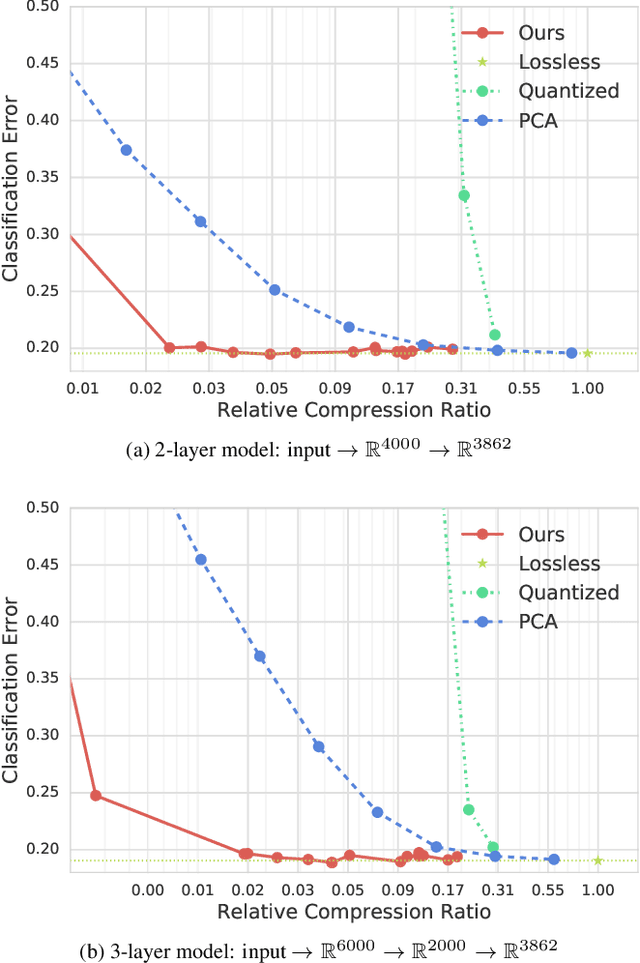
Pre-trained convolutional neural networks (CNNs) are powerful off-the-shelf feature generators and have been shown to perform very well on a variety of tasks. Unfortunately, the generated features are high dimensional and expensive to store: potentially hundreds of thousands of floats per example when processing videos. Traditional entropy based lossless compression methods are of little help as they do not yield desired level of compression, while general purpose lossy compression methods based on energy compaction (e.g. PCA followed by quantization and entropy coding) are sub-optimal, as they are not tuned to task specific objective. We propose a learned method that jointly optimizes for compressibility along with the task objective for learning the features. The plug-in nature of our method makes it straight-forward to integrate with any target objective and trade-off against compressibility. We present results on multiple benchmarks and demonstrate that our method produces features that are an order of magnitude more compressible, while having a regularization effect that leads to a consistent improvement in accuracy.