Implicit SVD for Graph Representation Learning

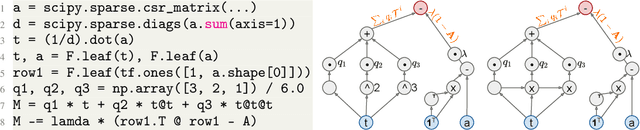
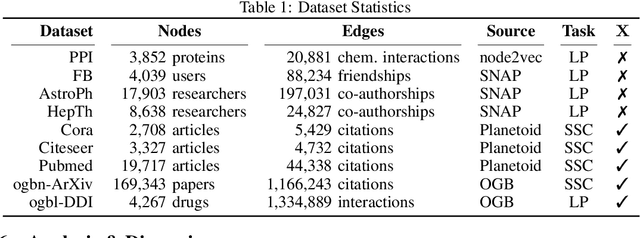
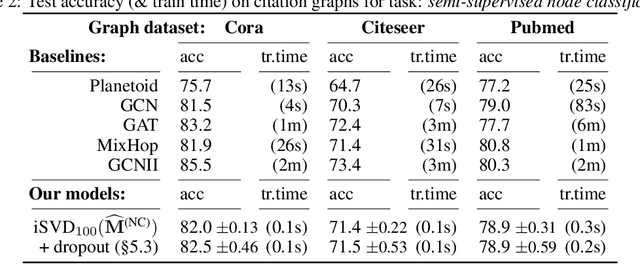
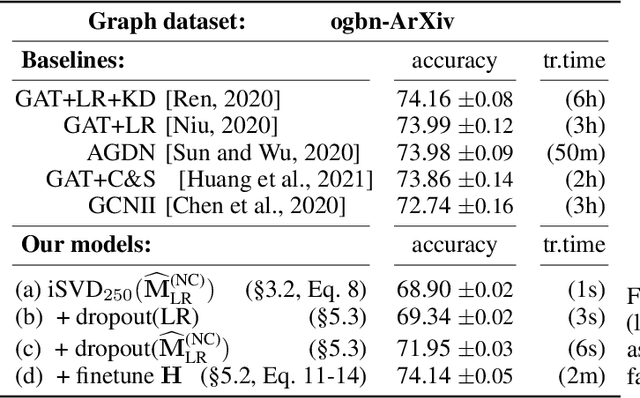
Recent improvements in the performance of state-of-the-art (SOTA) methods for Graph Representational Learning (GRL) have come at the cost of significant computational resource requirements for training, e.g., for calculating gradients via backprop over many data epochs. Meanwhile, Singular Value Decomposition (SVD) can find closed-form solutions to convex problems, using merely a handful of epochs. In this paper, we make GRL more computationally tractable for those with modest hardware. We design a framework that computes SVD of \textit{implicitly} defined matrices, and apply this framework to several GRL tasks. For each task, we derive linear approximation of a SOTA model, where we design (expensive-to-store) matrix $\mathbf{M}$ and train the model, in closed-form, via SVD of $\mathbf{M}$, without calculating entries of $\mathbf{M}$. By converging to a unique point in one step, and without calculating gradients, our models show competitive empirical test performance over various graphs such as article citation and biological interaction networks. More importantly, SVD can initialize a deeper model, that is architected to be non-linear almost everywhere, though behaves linearly when its parameters reside on a hyperplane, onto which SVD initializes. The deeper model can then be fine-tuned within only a few epochs. Overall, our procedure trains hundreds of times faster than state-of-the-art methods, while competing on empirical test performance. We open-source our implementation at: https://github.com/samihaija/isvd

Fast Graph Learning with Unique Optimal Solutions

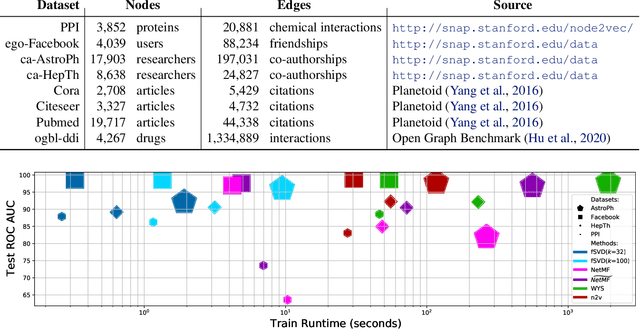
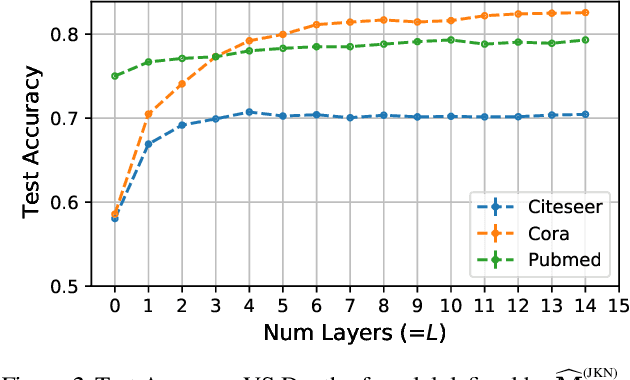
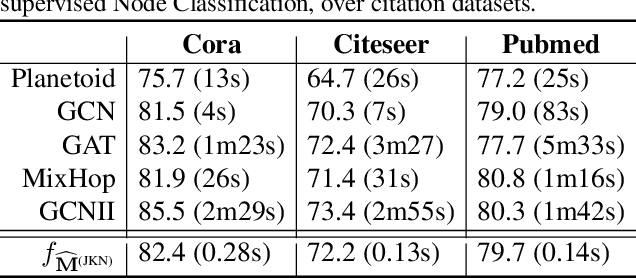
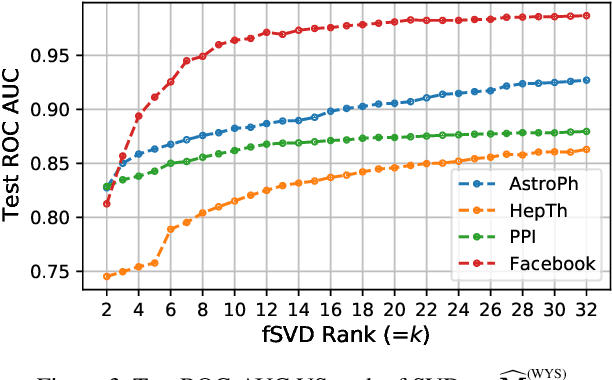
Graph Representation Learning (GRL) has been advancing at an unprecedented rate. However, many results rely on careful design and tuning of architectures, objectives, and training schemes. We propose efficient GRL methods that optimize convexified objectives with known closed form solutions. Guaranteed convergence to a global optimum releases practitioners from hyper-parameter and architecture tuning. Nevertheless, our proposed method achieves competitive or state-of-the-art performance on popular GRL tasks while providing orders of magnitude speedup. Although the design matrix ($\mathbf{M}$) of our objective is expensive to compute, we exploit results from random matrix theory to approximate solutions in linear time while avoiding an explicit calculation of $\mathbf{M}$. Our code is online: http://github.com/samihaija/tf-fsvd

Attacking and Defending Covert Channels and Behavioral Models

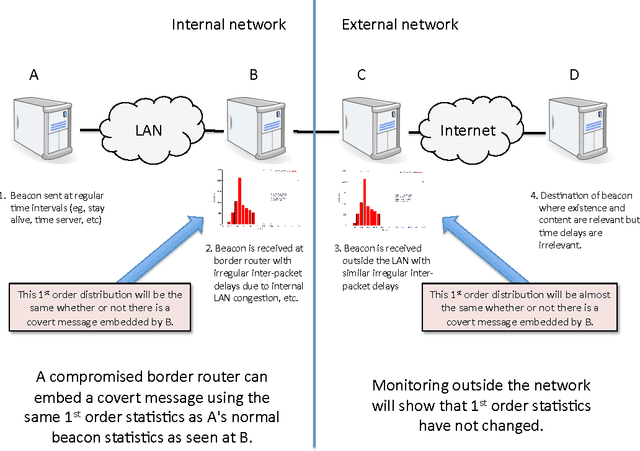
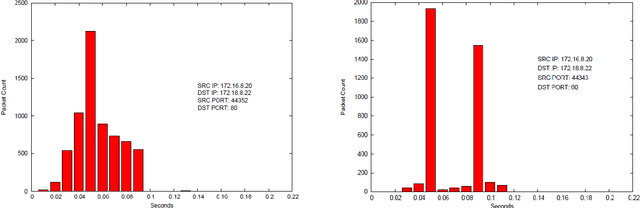
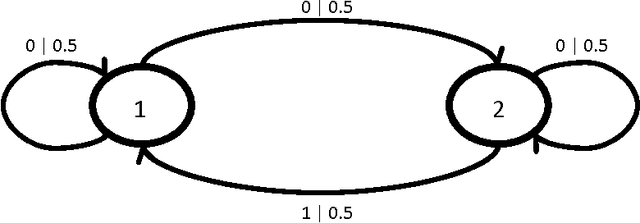
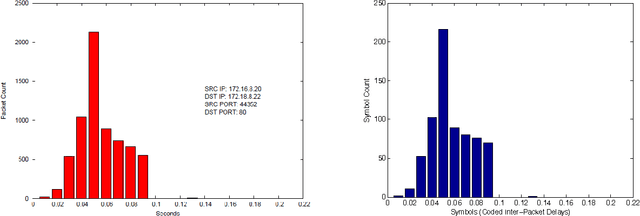
In this paper we present methods for attacking and defending $k$-gram statistical analysis techniques that are used, for example, in network traffic analysis and covert channel detection. The main new result is our demonstration of how to use a behavior's or process' $k$-order statistics to build a stochastic process that has those same $k$-order stationary statistics but possesses different, deliberately designed, $(k+1)$-order statistics if desired. Such a model realizes a "complexification" of the process or behavior which a defender can use to monitor whether an attacker is shaping the behavior. By deliberately introducing designed $(k+1)$-order behaviors, the defender can check to see if those behaviors are present in the data. We also develop constructs for source codes that respect the $k$-order statistics of a process while encoding covert information. One fundamental consequence of these results is that certain types of behavior analyses techniques come down to an {\em arms race} in the sense that the advantage goes to the party that has more computing resources applied to the problem.

Learning Hidden Markov Models using Non-Negative Matrix Factorization

The Baum-Welsh algorithm together with its derivatives and variations has been the main technique for learning Hidden Markov Models (HMM) from observational data. We present an HMM learning algorithm based on the non-negative matrix factorization (NMF) of higher order Markovian statistics that is structurally different from the Baum-Welsh and its associated approaches. The described algorithm supports estimation of the number of recurrent states of an HMM and iterates the non-negative matrix factorization (NMF) algorithm to improve the learned HMM parameters. Numerical examples are provided as well.