TEL'M: Test and Evaluation of Language Models

Language Models have demonstrated remarkable capabilities on some tasks while failing dramatically on others. The situation has generated considerable interest in understanding and comparing the capabilities of various Language Models (LMs) but those efforts have been largely ad hoc with results that are often little more than anecdotal. This is in stark contrast with testing and evaluation processes used in healthcare, radar signal processing, and other defense areas. In this paper, we describe Test and Evaluation of Language Models (TEL'M) as a principled approach for assessing the value of current and future LMs focused on high-value commercial, government and national security applications. We believe that this methodology could be applied to other Artificial Intelligence (AI) technologies as part of the larger goal of "industrializing" AI.

A Survey of Neural Networks and Formal Languages

This report is a survey of the relationships between various state-of-the-art neural network architectures and formal languages as, for example, structured by the Chomsky Language Hierarchy. Of particular interest are the abilities of a neural architecture to represent, recognize and generate words from a specific language by learning from samples of the language.

Analytic Properties of Trackable Weak Models

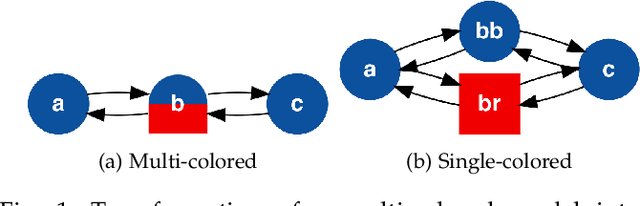
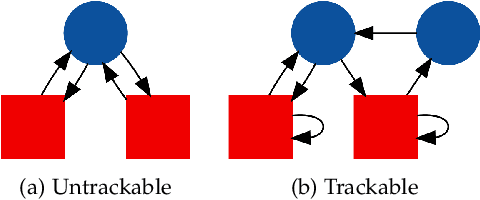
We present several new results on the feasibility of inferring the hidden states in strongly-connected trackable weak models. Here, a weak model is a directed graph in which each node is assigned a set of colors which may be emitted when that node is visited. A hypothesis is a node sequence which is consistent with a given color sequence. A weak model is said to be trackable if the worst case number of such hypotheses grows as a polynomial in the sequence length. We show that the number of hypotheses in strongly-connected trackable models is bounded by a constant and give an expression for this constant. We also consider the problem of reconstructing which branch was taken at a node with same-colored out-neighbors, and show that it is always eventually possible to identify which branch was taken if the model is strongly connected and trackable. We illustrate these properties by assigning transition probabilities and employing standard tools for analyzing Markov chains. In addition, we present new results for the entropy rates of weak models according to whether they are trackable or not. These theorems indicate that the combination of trackability and strong connectivity dramatically simplifies the task of reconstructing which nodes were visited. This work has implications for any problem which can be described in terms of an agent traversing a colored graph, such as the reconstruction of hidden states in a hidden Markov model (HMM).

Observability Properties of Colored Graphs

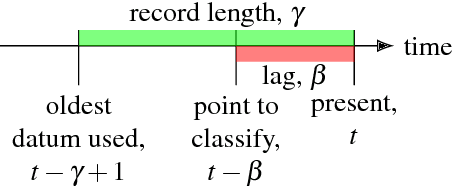
A colored graph is a directed graph in which either nodes or edges have been assigned colors that are not necessarily unique. Observability problems in such graphs are concerned with whether an agent observing the colors of edges or nodes traversed on a path in the graph can determine which node they are at currently or which nodes they have visited earlier in the path traversal. Previous research efforts have identified several different notions of observability as well as the associated properties of colored graphs for which those types of observability properties hold. This paper unifies the prior work into a common framework with several new analytic results about relationships between those notions and associated graph properties. The new framework provides an intuitive way to reason about the attainable path reconstruction accuracy as a function of lag and time spent observing, and identifies simple modifications that improve the observability properties of a given graph. This intuition is borne out in a series of numerical experiments. This work has implications for problems that can be described in terms of an agent traversing a colored graph, including the reconstruction of hidden states in a hidden Markov model (HMM).

Attacking and Defending Covert Channels and Behavioral Models

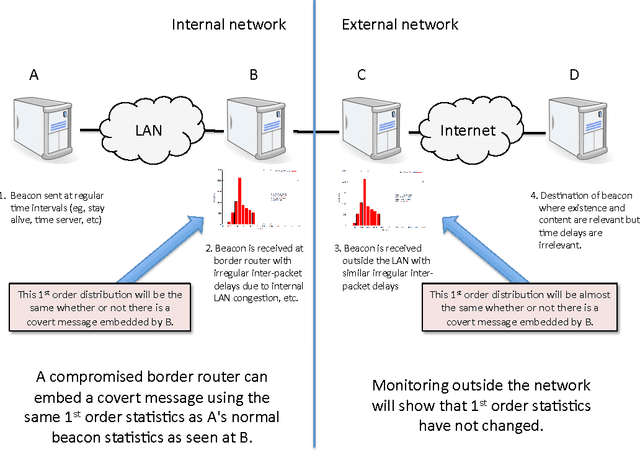
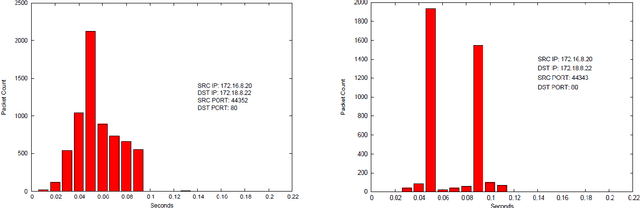
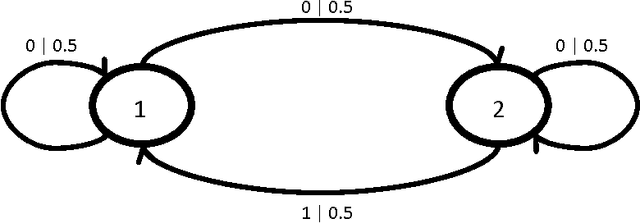
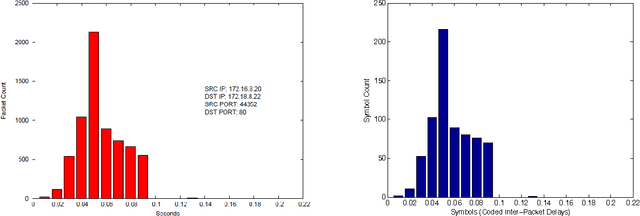
In this paper we present methods for attacking and defending $k$-gram statistical analysis techniques that are used, for example, in network traffic analysis and covert channel detection. The main new result is our demonstration of how to use a behavior's or process' $k$-order statistics to build a stochastic process that has those same $k$-order stationary statistics but possesses different, deliberately designed, $(k+1)$-order statistics if desired. Such a model realizes a "complexification" of the process or behavior which a defender can use to monitor whether an attacker is shaping the behavior. By deliberately introducing designed $(k+1)$-order behaviors, the defender can check to see if those behaviors are present in the data. We also develop constructs for source codes that respect the $k$-order statistics of a process while encoding covert information. One fundamental consequence of these results is that certain types of behavior analyses techniques come down to an {\em arms race} in the sense that the advantage goes to the party that has more computing resources applied to the problem.

Learning Hidden Markov Models using Non-Negative Matrix Factorization

The Baum-Welsh algorithm together with its derivatives and variations has been the main technique for learning Hidden Markov Models (HMM) from observational data. We present an HMM learning algorithm based on the non-negative matrix factorization (NMF) of higher order Markovian statistics that is structurally different from the Baum-Welsh and its associated approaches. The described algorithm supports estimation of the number of recurrent states of an HMM and iterates the non-negative matrix factorization (NMF) algorithm to improve the learned HMM parameters. Numerical examples are provided as well.