Analytic Properties of Trackable Weak Models
Paper and Code
Jan 08, 2020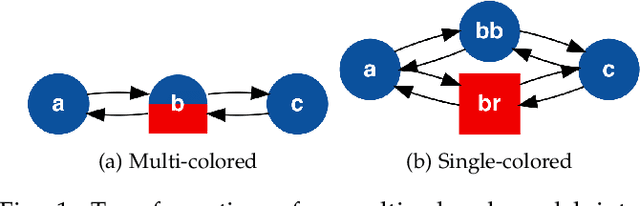

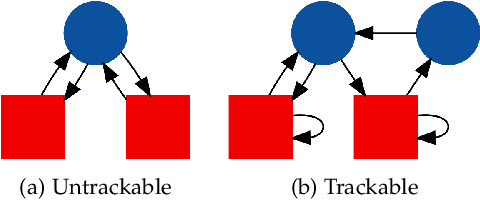

We present several new results on the feasibility of inferring the hidden states in strongly-connected trackable weak models. Here, a weak model is a directed graph in which each node is assigned a set of colors which may be emitted when that node is visited. A hypothesis is a node sequence which is consistent with a given color sequence. A weak model is said to be trackable if the worst case number of such hypotheses grows as a polynomial in the sequence length. We show that the number of hypotheses in strongly-connected trackable models is bounded by a constant and give an expression for this constant. We also consider the problem of reconstructing which branch was taken at a node with same-colored out-neighbors, and show that it is always eventually possible to identify which branch was taken if the model is strongly connected and trackable. We illustrate these properties by assigning transition probabilities and employing standard tools for analyzing Markov chains. In addition, we present new results for the entropy rates of weak models according to whether they are trackable or not. These theorems indicate that the combination of trackability and strong connectivity dramatically simplifies the task of reconstructing which nodes were visited. This work has implications for any problem which can be described in terms of an agent traversing a colored graph, such as the reconstruction of hidden states in a hidden Markov model (HMM).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge