Attacking and Defending Covert Channels and Behavioral Models
Paper and Code
Apr 27, 2011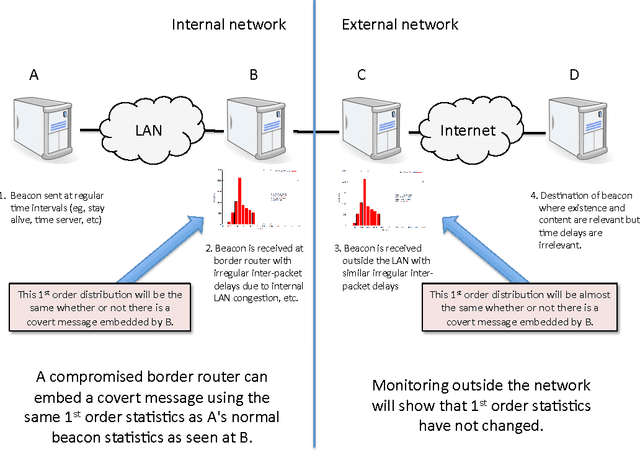
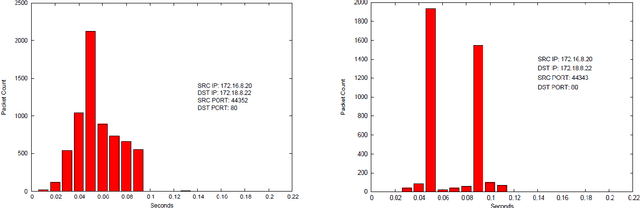
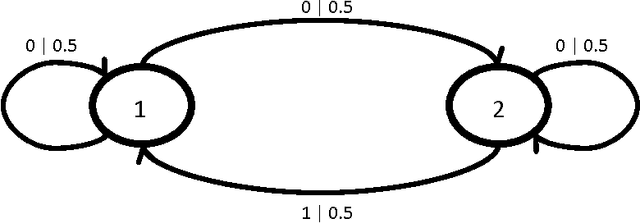
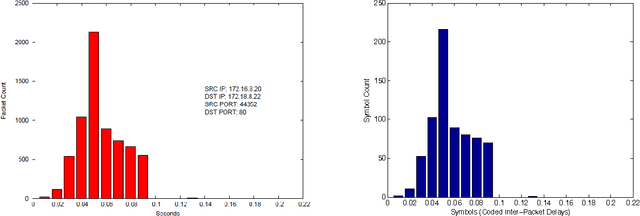
In this paper we present methods for attacking and defending $k$-gram statistical analysis techniques that are used, for example, in network traffic analysis and covert channel detection. The main new result is our demonstration of how to use a behavior's or process' $k$-order statistics to build a stochastic process that has those same $k$-order stationary statistics but possesses different, deliberately designed, $(k+1)$-order statistics if desired. Such a model realizes a "complexification" of the process or behavior which a defender can use to monitor whether an attacker is shaping the behavior. By deliberately introducing designed $(k+1)$-order behaviors, the defender can check to see if those behaviors are present in the data. We also develop constructs for source codes that respect the $k$-order statistics of a process while encoding covert information. One fundamental consequence of these results is that certain types of behavior analyses techniques come down to an {\em arms race} in the sense that the advantage goes to the party that has more computing resources applied to the problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge