Demand Forecasting from Spatiotemporal Data with Graph Networks and Temporal-Guided Embedding

Short-term demand forecasting models commonly combine convolutional and recurrent layers to extract complex spatiotemporal patterns in data. Long-term histories are also used to consider periodicity and seasonality patterns as time series data. In this study, we propose an efficient architecture, Temporal-Guided Network (TGNet), which utilizes graph networks and temporal-guided embedding. Graph networks extract invariant features to permutations of adjacent regions instead of convolutional layers. Temporal-guided embedding explicitly learns temporal contexts from training data and is substituted for the input of long-term histories from days/weeks ago. TGNet learns an autoregressive model, conditioned on temporal contexts of forecasting targets from temporal-guided embedding. Finally, our model achieves competitive performances with other baselines on three spatiotemporal demand dataset from real-world, but the number of trainable parameters is about 20 times smaller than a state-of-the-art baseline. We also show that temporal-guided embedding learns temporal contexts as intended and TGNet has robust forecasting performances even to atypical event situations.

Training Well-Generalizing Classifiers for Fairness Metrics and Other Data-Dependent Constraints

Classifiers can be trained with data-dependent constraints to satisfy fairness goals, reduce churn, achieve a targeted false positive rate, or other policy goals. We study the generalization performance for such constrained optimization problems, in terms of how well the constraints are satisfied at evaluation time, given that they are satisfied at training time. To improve generalization performance, we frame the problem as a two-player game where one player optimizes the model parameters on a training dataset, and the other player enforces the constraints on an independent validation dataset. We build on recent work in two-player constrained optimization to show that if one uses this two-dataset approach, then constraint generalization can be significantly improved. As we illustrate experimentally, this approach works not only in theory, but also in practice.

Optimization with Non-Differentiable Constraints with Applications to Fairness, Recall, Churn, and Other Goals

We show that many machine learning goals, such as improved fairness metrics, can be expressed as constraints on the model's predictions, which we call rate constraints. We study the problem of training non-convex models subject to these rate constraints (or any non-convex and non-differentiable constraints). In the non-convex setting, the standard approach of Lagrange multipliers may fail. Furthermore, if the constraints are non-differentiable, then one cannot optimize the Lagrangian with gradient-based methods. To solve these issues, we introduce the proxy-Lagrangian formulation. This new formulation leads to an algorithm that produces a stochastic classifier by playing a two-player non-zero-sum game solving for what we call a semi-coarse correlated equilibrium, which in turn corresponds to an approximately optimal and feasible solution to the constrained optimization problem. We then give a procedure which shrinks the randomized solution down to one that is a mixture of at most $m+1$ deterministic solutions, given $m$ constraints. This culminates in algorithms that can solve non-convex constrained optimization problems with possibly non-differentiable and non-convex constraints with theoretical guarantees. We provide extensive experimental results enforcing a wide range of policy goals including different fairness metrics, and other goals on accuracy, coverage, recall, and churn.

Quit When You Can: Efficient Evaluation of Ensembles with Ordering Optimization

Given a classifier ensemble and a set of examples to be classified, many examples may be confidently and accurately classified after only a subset of the base models in the ensemble are evaluated. This can reduce both mean latency and CPU while maintaining the high accuracy of the original ensemble. To achieve such gains, we propose jointly optimizing a fixed evaluation order of the base models and early-stopping thresholds. Our proposed objective is a combinatorial optimization problem, but we provide a greedy algorithm that achieves a 4-approximation of the optimal solution for certain cases. For those cases, this is also the best achievable polynomial time approximation bound unless $P = NP$. Experiments on benchmark and real-world problems show that the proposed Quit When You Can (QWYC) algorithm can speed-up average evaluation time by $2$x--$4$x, and is around $1.5$x faster than prior work. QWYC's joint optimization of ordering and thresholds also performed better in experiments than various fixed orderings, including gradient boosted trees' ordering.

Deep Lattice Networks and Partial Monotonic Functions

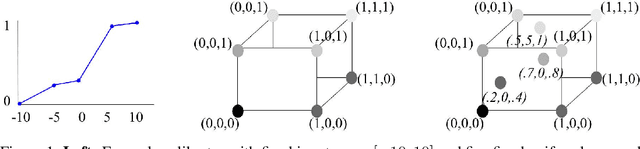
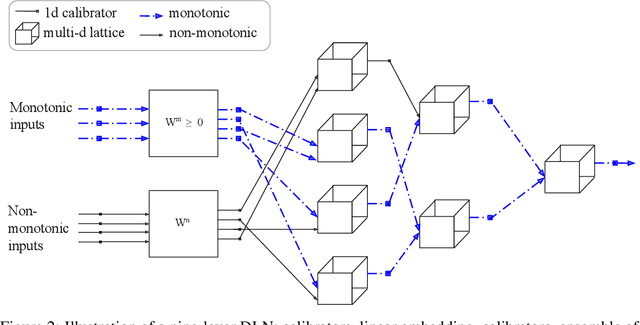
We propose learning deep models that are monotonic with respect to a user-specified set of inputs by alternating layers of linear embeddings, ensembles of lattices, and calibrators (piecewise linear functions), with appropriate constraints for monotonicity, and jointly training the resulting network. We implement the layers and projections with new computational graph nodes in TensorFlow and use the ADAM optimizer and batched stochastic gradients. Experiments on benchmark and real-world datasets show that six-layer monotonic deep lattice networks achieve state-of-the art performance for classification and regression with monotonicity guarantees.