Reward Learning as Doubly Nonparametric Bandits: Optimal Design and Scaling Laws

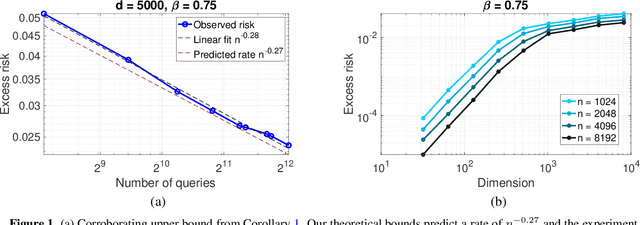
Specifying reward functions for complex tasks like object manipulation or driving is challenging to do by hand. Reward learning seeks to address this by learning a reward model using human feedback on selected query policies. This shifts the burden of reward specification to the optimal design of the queries. We propose a theoretical framework for studying reward learning and the associated optimal experiment design problem. Our framework models rewards and policies as nonparametric functions belonging to subsets of Reproducing Kernel Hilbert Spaces (RKHSs). The learner receives (noisy) oracle access to a true reward and must output a policy that performs well under the true reward. For this setting, we first derive non-asymptotic excess risk bounds for a simple plug-in estimator based on ridge regression. We then solve the query design problem by optimizing these risk bounds with respect to the choice of query set and obtain a finite sample statistical rate, which depends primarily on the eigenvalue spectrum of a certain linear operator on the RKHSs. Despite the generality of these results, our bounds are stronger than previous bounds developed for more specialized problems. We specifically show that the well-studied problem of Gaussian process (GP) bandit optimization is a special case of our framework, and that our bounds either improve or are competitive with known regret guarantees for the Mat\'ern kernel.

Leveraging Reviews: Learning to Price with Buyer and Seller Uncertainty

In online marketplaces, customers have access to hundreds of reviews for a single product. Buyers often use reviews from other customers that share their type -- such as height for clothing, skin type for skincare products, and location for outdoor furniture -- to estimate their values, which they may not know a priori. Customers with few relevant reviews may hesitate to make a purchase except at a low price, so for the seller, there is a tension between setting high prices and ensuring that there are enough reviews so that buyers can confidently estimate their values. Simultaneously, sellers may use reviews to gauge the demand for items they wish to sell. In this work, we study this pricing problem in an online setting where the seller interacts with a set of buyers of finitely-many types, one-by-one, over a series of $T$ rounds. At each round, the seller first sets a price. Then a buyer arrives and examines the reviews of the previous buyers with the same type, which reveal those buyers' ex-post values. Based on the reviews, the buyer decides to purchase if they have good reason to believe that their ex-ante utility is positive. Crucially, the seller does not know the buyer's type when setting the price, nor even the distribution over types. We provide a no-regret algorithm that the seller can use to obtain high revenue. When there are $d$ types, after $T$ rounds, our algorithm achieves a problem-independent $\tilde O(T^{2/3}d^{1/3})$ regret bound. However, when the smallest probability $q_{\text{min}}$ that any given type appears is large, specifically when $q_{\text{min}} \in \Omega(d^{-2/3}T^{-1/3})$, then the same algorithm achieves a $\tilde O(T^{1/2}q_{\text{min}}^{-1/2})$ regret bound. We complement these upper bounds with matching lower bounds in both regimes, showing that our algorithm is minimax optimal up to lower order terms.

Mechanisms that Incentivize Data Sharing in Federated Learning

Federated learning is typically considered a beneficial technology which allows multiple agents to collaborate with each other, improve the accuracy of their models, and solve problems which are otherwise too data-intensive / expensive to be solved individually. However, under the expectation that other agents will share their data, rational agents may be tempted to engage in detrimental behavior such as free-riding where they contribute no data but still enjoy an improved model. In this work, we propose a framework to analyze the behavior of such rational data generators. We first show how a naive scheme leads to catastrophic levels of free-riding where the benefits of data sharing are completely eroded. Then, using ideas from contract theory, we introduce accuracy shaping based mechanisms to maximize the amount of data generated by each agent. These provably prevent free-riding without needing any payment mechanism.

Off-Policy Evaluation with Policy-Dependent Optimization Response

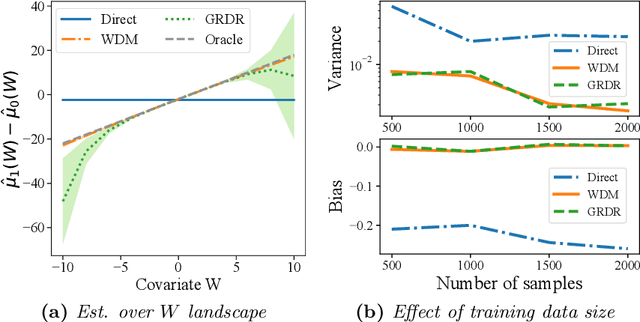
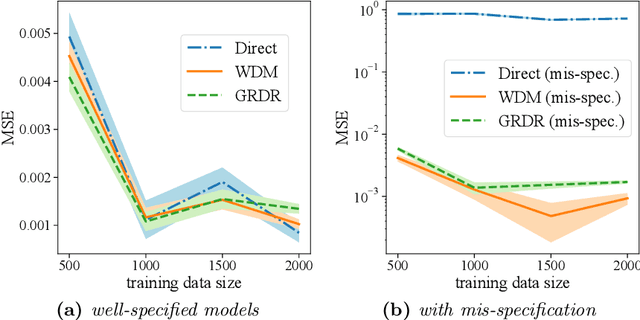
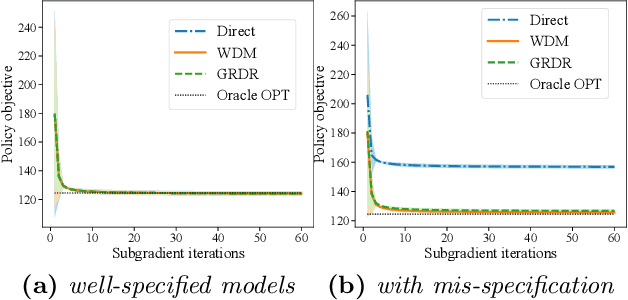
The intersection of causal inference and machine learning for decision-making is rapidly expanding, but the default decision criterion remains an \textit{average} of individual causal outcomes across a population. In practice, various operational restrictions ensure that a decision-maker's utility is not realized as an \textit{average} but rather as an \textit{output} of a downstream decision-making problem (such as matching, assignment, network flow, minimizing predictive risk). In this work, we develop a new framework for off-policy evaluation with a \textit{policy-dependent} linear optimization response: causal outcomes introduce stochasticity in objective function coefficients. In this framework, a decision-maker's utility depends on the policy-dependent optimization, which introduces a fundamental challenge of \textit{optimization} bias even for the case of policy evaluation. We construct unbiased estimators for the policy-dependent estimand by a perturbation method. We also discuss the asymptotic variance properties for a set of plug-in regression estimators adjusted to be compatible with that perturbation method. Lastly, attaining unbiased policy evaluation allows for policy optimization, and we provide a general algorithm for optimizing causal interventions. We corroborate our theoretical results with numerical simulations.

Partial Identification with Noisy Covariates: A Robust Optimization Approach

Causal inference from observational datasets often relies on measuring and adjusting for covariates. In practice, measurements of the covariates can often be noisy and/or biased, or only measurements of their proxies may be available. Directly adjusting for these imperfect measurements of the covariates can lead to biased causal estimates. Moreover, without additional assumptions, the causal effects are not point-identifiable due to the noise in these measurements. To this end, we study the partial identification of causal effects given noisy covariates, under a user-specified assumption on the noise level. The key observation is that we can formulate the identification of the average treatment effects (ATE) as a robust optimization problem. This formulation leads to an efficient robust optimization algorithm that bounds the ATE with noisy covariates. We show that this robust optimization approach can extend a wide range of causal adjustment methods to perform partial identification, including backdoor adjustment, inverse propensity score weighting, double machine learning, and front door adjustment. Across synthetic and real datasets, we find that this approach provides ATE bounds with a higher coverage probability than existing methods.

No-Regret Learning in Partially-Informed Auctions

Auctions with partially-revealed information about items are broadly employed in real-world applications, but the underlying mechanisms have limited theoretical support. In this work, we study a machine learning formulation of these types of mechanisms, presenting algorithms that are no-regret from the buyer's perspective. Specifically, a buyer who wishes to maximize his utility interacts repeatedly with a platform over a series of $T$ rounds. In each round, a new item is drawn from an unknown distribution and the platform publishes a price together with incomplete, "masked" information about the item. The buyer then decides whether to purchase the item. We formalize this problem as an online learning task where the goal is to have low regret with respect to a myopic oracle that has perfect knowledge of the distribution over items and the seller's masking function. When the distribution over items is known to the buyer and the mask is a SimHash function mapping $\mathbb{R}^d$ to $\{0,1\}^{\ell}$, our algorithm has regret $\tilde {\mathcal{O}}((Td\ell)^{\frac{1}{2}})$. In a fully agnostic setting when the mask is an arbitrary function mapping to a set of size $n$, our algorithm has regret $\tilde {\mathcal{O}}(T^{\frac{3}{4}}n^{\frac{1}{2}})$. Finally, when the prices are stochastic, the algorithm has regret $\tilde {\mathcal{O}}((Tn)^{\frac{1}{2}})$.

Robust Learning of Optimal Auctions

We study the problem of learning revenue-optimal multi-bidder auctions from samples when the samples of bidders' valuations can be adversarially corrupted or drawn from distributions that are adversarially perturbed. First, we prove tight upper bounds on the revenue we can obtain with a corrupted distribution under a population model, for both regular valuation distributions and distributions with monotone hazard rate (MHR). We then propose new algorithms that, given only an ``approximate distribution'' for the bidder's valuation, can learn a mechanism whose revenue is nearly optimal simultaneously for all ``true distributions'' that are $\alpha$-close to the original distribution in Kolmogorov-Smirnov distance. The proposed algorithms operate beyond the setting of bounded distributions that have been studied in prior works, and are guaranteed to obtain a fraction $1-O(\alpha)$ of the optimal revenue under the true distribution when the distributions are MHR. Moreover, they are guaranteed to yield at least a fraction $1-O(\sqrt{\alpha})$ of the optimal revenue when the distributions are regular. We prove that these upper bounds cannot be further improved, by providing matching lower bounds. Lastly, we derive sample complexity upper bounds for learning a near-optimal auction for both MHR and regular distributions.

Learning from an Exploring Demonstrator: Optimal Reward Estimation for Bandits

We introduce the "inverse bandit" problem of estimating the rewards of a multi-armed bandit instance from observing the learning process of a low-regret demonstrator. Existing approaches to the related problem of inverse reinforcement learning assume the execution of an optimal policy, and thereby suffer from an identifiability issue. In contrast, our paradigm leverages the demonstrator's behavior en route to optimality, and in particular, the exploration phase, to obtain consistent reward estimates. We develop simple and efficient reward estimation procedures for demonstrations within a class of upper-confidence-based algorithms, showing that reward estimation gets progressively easier as the regret of the algorithm increases. We match these upper bounds with information-theoretic lower bounds that apply to any demonstrator algorithm, thereby characterizing the optimal tradeoff between exploration and reward estimation. Extensive empirical evaluations on both synthetic data and simulated experimental design data from the natural sciences corroborate our theoretical results.

The Stereotyping Problem in Collaboratively Filtered Recommender Systems

Recommender systems -- and especially matrix factorization-based collaborative filtering algorithms -- play a crucial role in mediating our access to online information. We show that such algorithms induce a particular kind of stereotyping: if preferences for a \textit{set} of items are anti-correlated in the general user population, then those items may not be recommended together to a user, regardless of that user's preferences and ratings history. First, we introduce a notion of \textit{joint accessibility}, which measures the extent to which a set of items can jointly be accessed by users. We then study joint accessibility under the standard factorization-based collaborative filtering framework, and provide theoretical necessary and sufficient conditions when joint accessibility is violated. Moreover, we show that these conditions can easily be violated when the users are represented by a single feature vector. To improve joint accessibility, we further propose an alternative modelling fix, which is designed to capture the diverse multiple interests of each user using a multi-vector representation. We conduct extensive experiments on real and simulated datasets, demonstrating the stereotyping problem with standard single-vector matrix factorization models.

Test-time Collective Prediction

An increasingly common setting in machine learning involves multiple parties, each with their own data, who want to jointly make predictions on future test points. Agents wish to benefit from the collective expertise of the full set of agents to make better predictions than they would individually, but may not be willing to release their data or model parameters. In this work, we explore a decentralized mechanism to make collective predictions at test time, leveraging each agent's pre-trained model without relying on external validation, model retraining, or data pooling. Our approach takes inspiration from the literature in social science on human consensus-making. We analyze our mechanism theoretically, showing that it converges to inverse meansquared-error (MSE) weighting in the large-sample limit. To compute error bars on the collective predictions we propose a decentralized Jackknife procedure that evaluates the sensitivity of our mechanism to a single agent's prediction. Empirically, we demonstrate that our scheme effectively combines models with differing quality across the input space. The proposed consensus prediction achieves significant gains over classical model averaging, and even outperforms weighted averaging schemes that have access to additional validation data.