Off-Policy Evaluation with Policy-Dependent Optimization Response

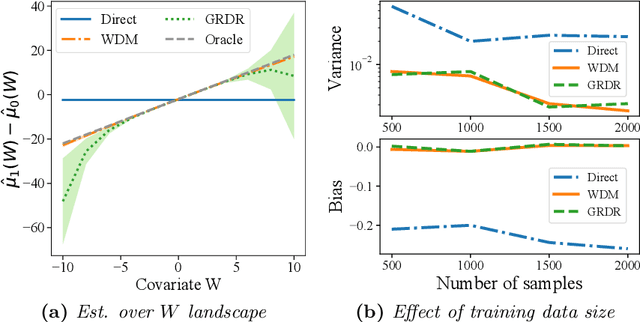
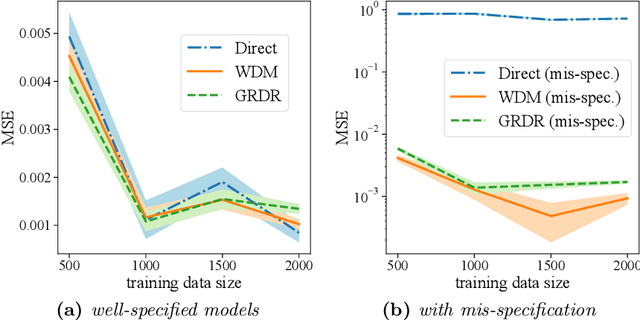
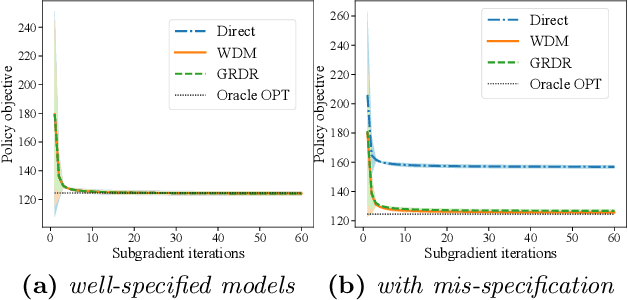
The intersection of causal inference and machine learning for decision-making is rapidly expanding, but the default decision criterion remains an \textit{average} of individual causal outcomes across a population. In practice, various operational restrictions ensure that a decision-maker's utility is not realized as an \textit{average} but rather as an \textit{output} of a downstream decision-making problem (such as matching, assignment, network flow, minimizing predictive risk). In this work, we develop a new framework for off-policy evaluation with a \textit{policy-dependent} linear optimization response: causal outcomes introduce stochasticity in objective function coefficients. In this framework, a decision-maker's utility depends on the policy-dependent optimization, which introduces a fundamental challenge of \textit{optimization} bias even for the case of policy evaluation. We construct unbiased estimators for the policy-dependent estimand by a perturbation method. We also discuss the asymptotic variance properties for a set of plug-in regression estimators adjusted to be compatible with that perturbation method. Lastly, attaining unbiased policy evaluation allows for policy optimization, and we provide a general algorithm for optimizing causal interventions. We corroborate our theoretical results with numerical simulations.