Robust Optimization for Fairness with Noisy Protected Groups
Paper and Code
Feb 21, 2020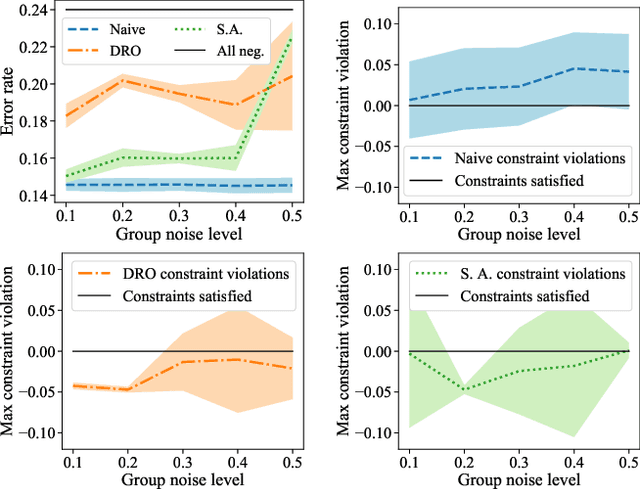
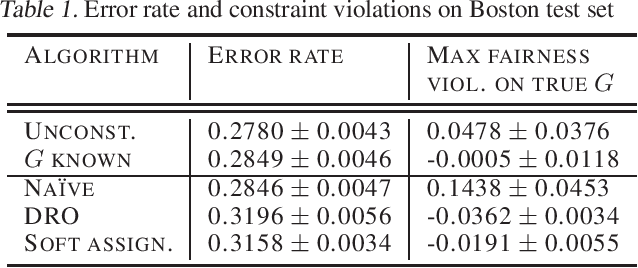

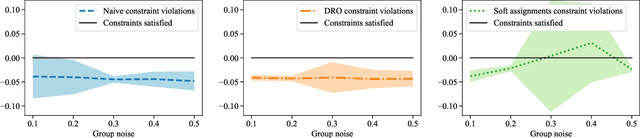
Many existing fairness criteria for machine learning involve equalizing or achieving some metric across \textit{protected groups} such as race or gender groups. However, practitioners trying to audit or enforce such group-based criteria can easily face the problem of noisy or biased protected group information. We study this important practical problem in two ways. First, we study the consequences of na{\"i}vely only relying on noisy protected groups: we provide an upper bound on the fairness violations on the true groups $G$ when the fairness criteria are satisfied on noisy groups $\hat{G}$. Second, we introduce two new approaches using robust optimization that, unlike the na{\"i}ve approach of only relying on $\hat{G}$, are guaranteed to satisfy fairness criteria on the true protected groups $G$ while minimizing a training objective. We provide theoretical guarantees that one such approach converges to an optimal feasible solution. Using two case studies, we empirically show that the robust approaches achieve better true group fairness guarantees than the na{\"i}ve approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge