Olexander Mangylov
Global Optimization Networks
Feb 02, 2022


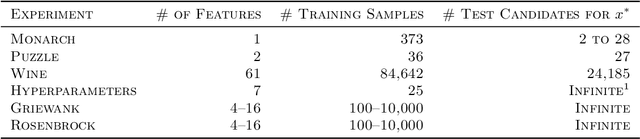
Abstract:We consider the problem of estimating a good maximizer of a black-box function given noisy examples. To solve such problems, we propose to fit a new type of function which we call a global optimization network (GON), defined as any composition of an invertible function and a unimodal function, whose unique global maximizer can be inferred in $\mathcal{O}(D)$ time. In this paper, we show how to construct invertible and unimodal functions by using linear inequality constraints on lattice models. We also extend to \emph{conditional} GONs that find a global maximizer conditioned on specified inputs of other dimensions. Experiments show the GON maximizers are statistically significantly better predictions than those produced by convex fits, GPR, or DNNs, and are more reasonable predictions for real-world problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge