Optimizing Black-box Metrics with Iterative Example Weighting

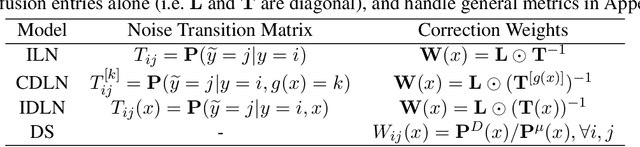
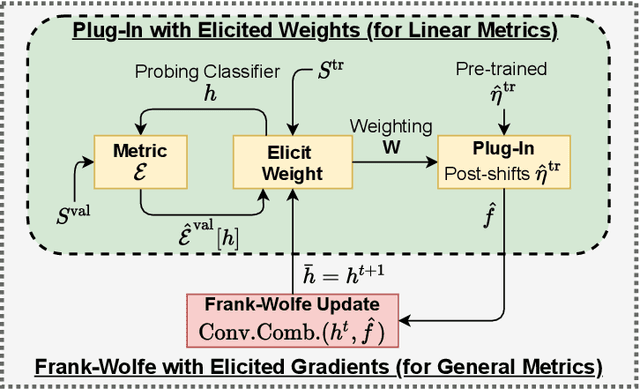
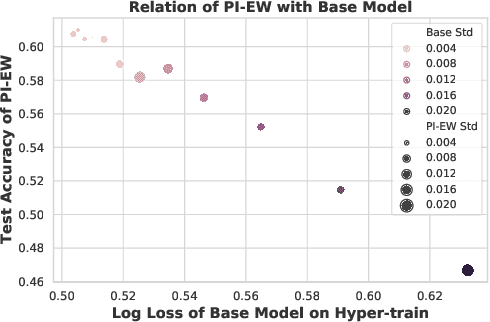
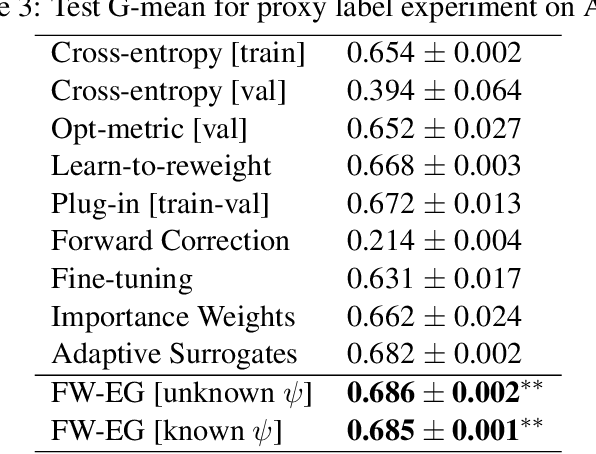
We consider learning to optimize a classification metric defined by a black-box function of the confusion matrix. Such black-box learning settings are ubiquitous, for example, when the learner only has query access to the metric of interest, or in noisy-label and domain adaptation applications where the learner must evaluate the metric via performance evaluation using a small validation sample. Our approach is to adaptively learn example weights on the training dataset such that the resulting weighted objective best approximates the metric on the validation sample. We show how to model and estimate the example weights and use them to iteratively post-shift a pre-trained class probability estimator to construct a classifier. We also analyze the resulting procedure's statistical properties. Experiments on various label noise, domain shift, and fair classification setups confirm that our proposal is better than the individual state-of-the-art baselines for each application.

Quadratic Metric Elicitation with Application to Fairness

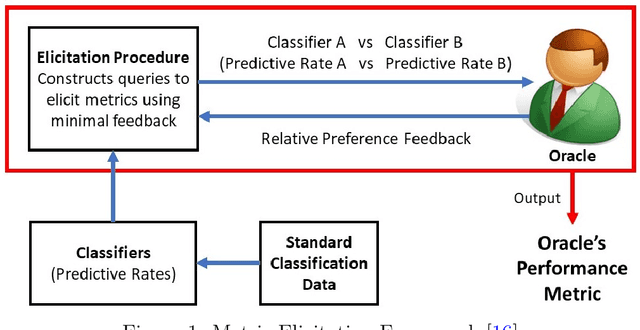
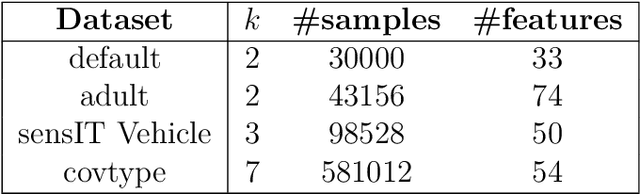
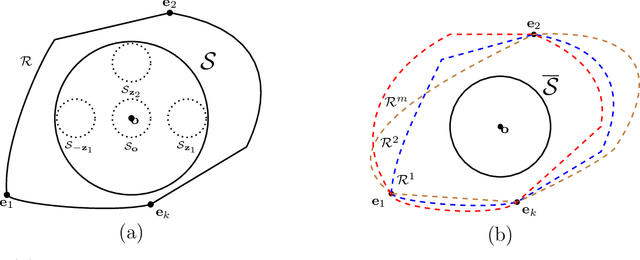
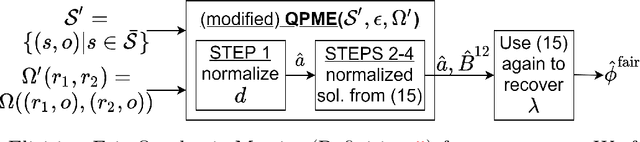
Metric elicitation is a recent framework for eliciting performance metrics that best reflect implicit user preferences. This framework enables a practitioner to adjust the performance metrics based on the application, context, and population at hand. However, available elicitation strategies have been limited to linear (or fractional-linear) functions of predictive rates. In this paper, we develop an approach to elicit from a wider range of complex multiclass metrics defined by quadratic functions of rates by exploiting their local linear structure. We apply this strategy to elicit quadratic metrics for group-based fairness, and also discuss how it can be generalized to higher-order polynomials. Our elicitation strategies require only relative preference feedback and are robust to both feedback and finite sample noise.